Khảo sát sự biến thiên và vẽ đồ thị hàm số - Từ điển mô.. 1. Cách tìm hàm đa thức bậc ba biết đồ thị hoặc bảng biến thiên
Cho đồ thị hàm số/bảng biến thiên của hàm bậc ba \(y = a{x^3} + b{x^2} + cx + d\) \((a,b,c,d \in \mathbb{R},a \ne 0)\).
Đồ thị hàm số có điểm cực trị là \(M\left( {{x_M};{y_M}} \right)\) thì \(\left\{ \begin{array}{l}f'\left( {{x_M}} \right) = 0\\f\left( {{x_M}} \right) = {y_M}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3a{x_M}^2 + 2b{x_M} + c{x_M} = 0\\a{x_M}^3 + b{x_M}^2 + c{x_M} + {d_M} = {y_M}\end{array} \right.\).
Đồ thị hàm số đi qua điểm \(A\left( {{x_A};{y_A}} \right)\) thì \(f\left( {{x_A}} \right) = {y_A} \Leftrightarrow a{x_A}^3 + b{x_A}^2 + c{x_A} + {d_A} = {y_A}\).
Ví dụ minh hoạ:
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên như hình vẽ sau:
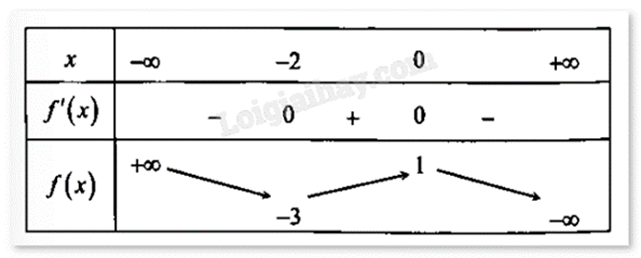
Xác định công thức của hàm số.
Giải:
Ta có: \(f'(x) = 3a{x^2} + 2bx + c\).
Đồ thị hàm số có hai điểm cực trị (0;1) và (−2;−3) nên ta có:
\(\left\{ {\begin{array}{*{20}{c}}{f'(0) = 0}\\{f(0) = 1}\\{f'( - 2) = 0}\\{f( - 2) = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{c = 0}\\{d = 1}\\{12a - 4b = 0}\\{ - 8a + 4b + 1 = - 3}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - 1}\\{b = - 3}\\{c = 0}\\{d = 1}\end{array}} \right.} \right.\)
Vậy hàm số cần tìm là \(y = - {x^3} - 3{x^2} + 1\).
2. Cách tìm hàm phân thức bậc nhất biết đồ thị hoặc bảng biến thiên
Cho đồ thị hàm số/bảng biến thiên của hàm phân thức bậc nhất \(y = \frac{{ax + b}}{{cx + d}}\) \((c \ne 0,ad - bc \ne 0)\).
Đường tiệm cận ngang: \(y = \frac{a}{c}\).
Đường tiệm cận đứng: \(x = - \frac{d}{c}\).
Đồ thị cắt trục Oy tại điểm có tung độ \(y = \frac{b}{d}\).
Đồ thị hàm số đi qua điểm \(A\left( {{x_A};{y_A}} \right)\) thì \(f\left( {{x_A}} \right) = {y_A} \Leftrightarrow \frac{{a{x_A} + b}}{{c{x_A} + d}} = {y_A}\).
Ví dụ minh hoạ:
Cho hàm số \(y = \frac{{ax + b}}{{x + c}}\) có đồ thị như hình vẽ; a, b, c là các số nguyên. Tính giá trị của biểu thức T = a – 3b + 2c.
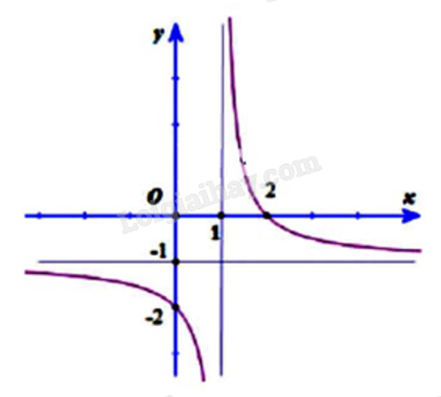
Đường tiệm cận ngang: \(y = - 1 \Leftrightarrow \frac{a}{1} = - 1 \Leftrightarrow a = - 1\).
Đường tiệm cận đứng: \(x = 1 \Leftrightarrow - c = 1 \Leftrightarrow c = - 1\).
Đồ thị cắt trục Oy tại điểm có tung độ \(y = - 2 \Leftrightarrow \frac{b}{c} = - 2 \Leftrightarrow \frac{b}{{ - 1}} = - 2 \Leftrightarrow b = 2\).
Vậy T = a – 3b + 2c = -1 – 3.2 + 2.(-1) = -9.
