Khảo sát sự biến thiên và vẽ đồ thị hàm số - Từ điển mô.. 1. Cách nhận dạng đồ thị hàm đa thức bậc ba chứa dấu giá trị tuyệt đối
Cách vẽ đồ thị y = |f(x)| từ đồ thị y = f(x).
- Giữ nguyên phần đồ thị phía trên trục Ox.
- Lấy đối xứng phần đồ thị phía dưới trục Ox qua Ox.
- Xoá phần đồ thị phía dưới Ox.
Cách vẽ đồ thị y = f(|x|) từ đồ thị y = f(x).
- Giữ nguyên phần đồ thị bên phải trục Oy.
- Xoá phần đồ thị bên trái trục Oy.
- Lấy đối xứng phần đồ thị bên phải trục Oy qua Oy.
Ví dụ minh hoạ:
a) Cho hàm số \(y = {x^3} - 3{x^2} + 2\) có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào?
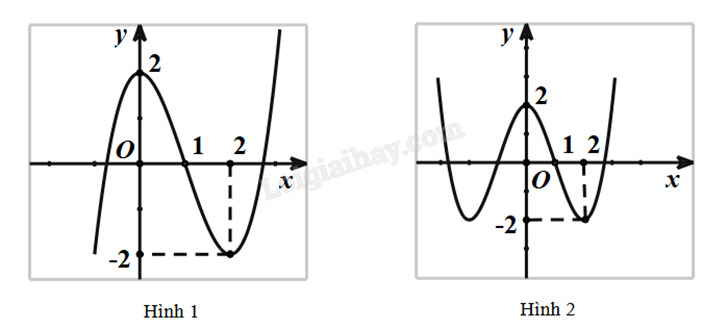
b) Cho hàm số \(y = {x^3} - 3{x^2} + 2\) có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào?
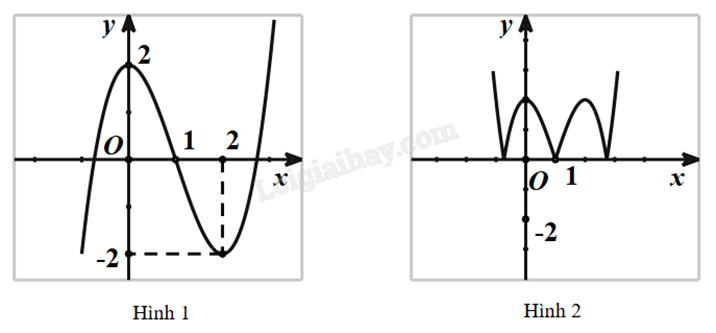
a) Từ đồ thị hình 1 sang đồ thị hình 2 ta thấy toàn bộ đồ thị phía “phải” Oy sau đó lấy đối xứng sang trái. Vậy đồ thị hình 2 là \(y = {\left| x \right|^3} - 3{\left| x \right|^2} + 2 \Leftrightarrow y = {\left| x \right|^3} - 3{x^2} + 2\).
b) Từ đồ thị hình 1 sang đồ thị hình 2 ta thấy toàn bộ đồ thị phía trên Ox được giữ nguyên, phần đồ thị phía dưới Ox được lấy đối xứng qua Ox. Vậy đồ thị hình 2 là \(y = \left| {{x^3} - 3{x^2} + 2} \right|\).
2. Cách nhận dạng đồ thị hàm phân thức bậc nhất chứa dấu giá trị tuyệt đối
Cách vẽ đồ thị \(y = \left| {\frac{{ax + b}}{{cx + d}}} \right|\) từ đồ thị \(y = \frac{{ax + b}}{{cx + d}}\):
- Giữ nguyên phần đồ thị phía trên trục Ox.
- Lấy đối xứng phần đồ thị phía dưới trục Ox qua Ox (lật từ dưới lên trên).
Cách vẽ đồ thị \(y = \frac{{a\left| x \right| + b}}{{c\left| x \right| + d}}\) từ đồ thị \(y = \frac{{ax + b}}{{cx + d}}\):
- Giữ nguyên phần đồ thị bên phải trục Oy.
- Lấy đối xứng phần đồ thị bên phải trục Oy qua Oy (lật từ phải qua trái).
Cách vẽ đồ thị \(y = \frac{{ax + b}}{{\left| {cx + d} \right|}}\) từ đồ thị \(y = \frac{{ax + b}}{{cx + d}}\)
- Giữ nguyên phần đồ thị bên phải đường thẳng \(x = - \frac{d}{c}\) (tiệm cận đứng).
- Lấy đối xứng phần đồ thị bên trái đường thẳng \(x = - \frac{d}{c}\) qua trục Ox (dưới lật lên trên, trên lật xuống dưới).
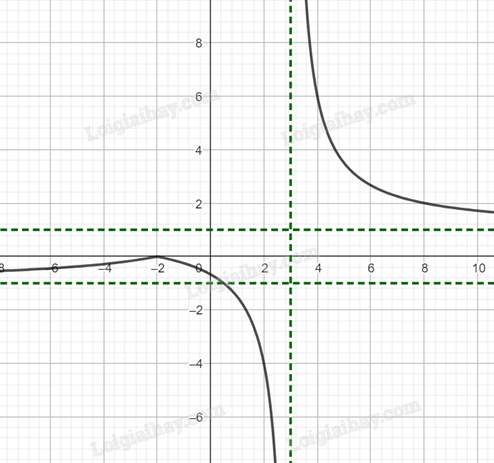
Cách vẽ đồ thị \(y = \frac{{\left| {ax + b} \right|}}{{cx + d}}\) từ đồ thị \(y = \frac{{ax + b}}{{cx + d}}\):
- Giữ nguyên phần đồ thị bên phải đường thẳng \(x = - \frac{b}{a}\).
- Lấy đối xứng phần đồ thị bên trái đường thẳng \(x = - \frac{b}{a}\) qua trục Ox (dưới lật lên trên, trên lật xuống dưới).
Ví dụ minh hoạ:
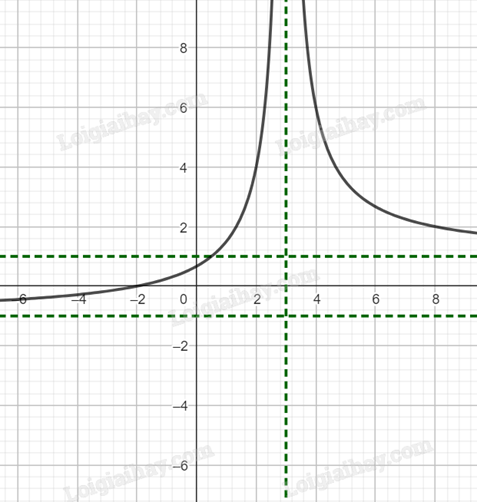
Ta có đồ thị của hàm số \(y = \frac{{x + 2}}{{x - 3}}\):
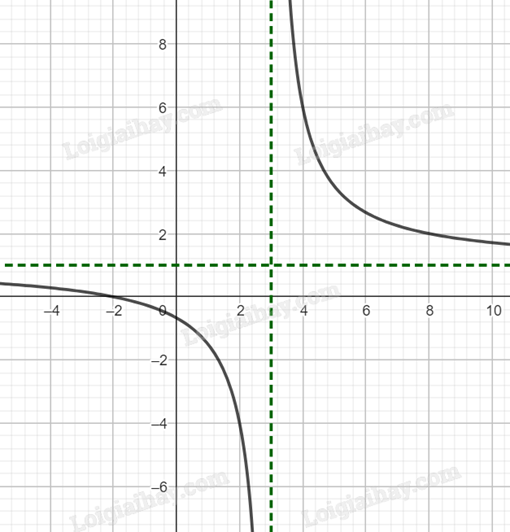
Vẽ đồ thị hàm số \(y = \left| {\frac{{x + 2}}{{x - 3}}} \right|\):
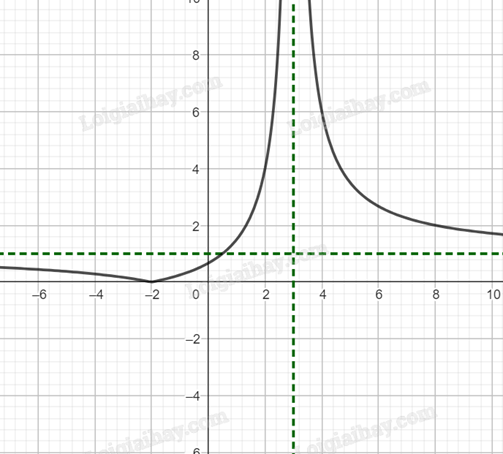
Vẽ đồ thị hàm số \(y = \frac{{\left| x \right| + 2}}{{\left| x \right| - 3}}\):
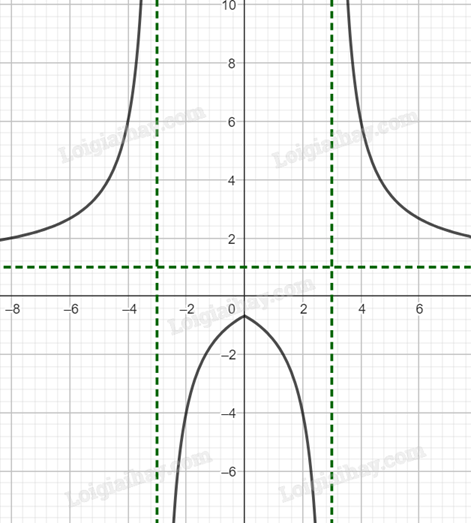
Vẽ đồ thị hàm số \(y = \frac{{x + 2}}{{\left| {x - 3} \right|}}\):
Vẽ đồ thị hàm số \(y = \frac{{\left| {x + 2} \right|}}{{x - 3}}\):
