1. Đường tiệm cận là gì?
a) Tiệm cận đứng:
Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thoả mãn:
\(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \).
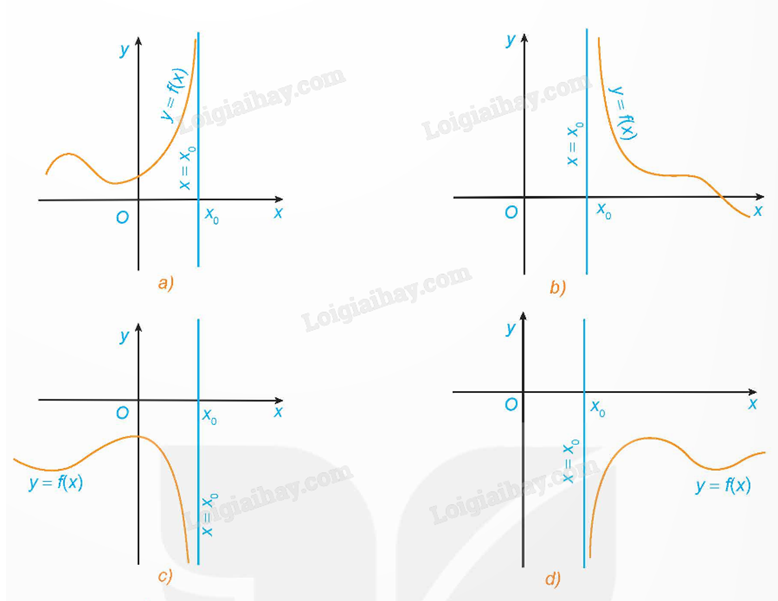
b) Tiệm cận ngang
Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu:
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = {y_0}\).
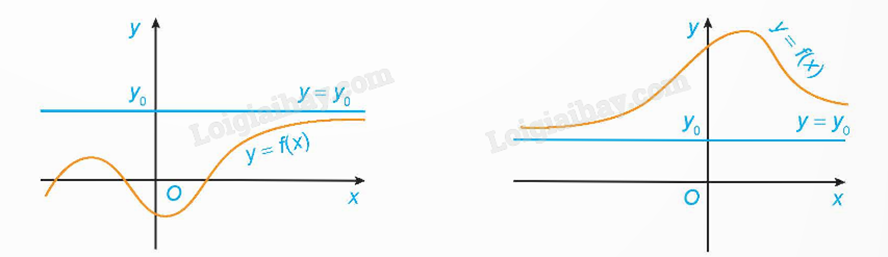
c) Tiệm cận xiên:
Đường thẳng y = ax + b \((a \ne 0)\) gọi là đường tiệm cận xiên của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\).
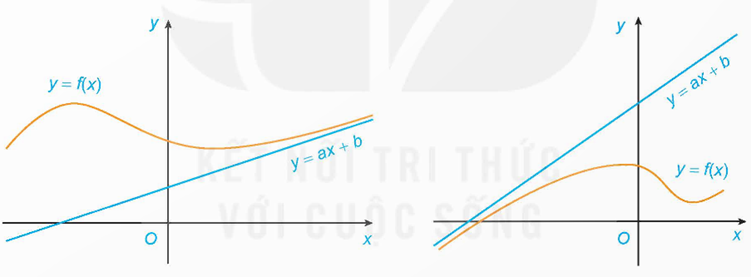
2. Cách giải bài toán thực tế liên quan đến tiệm cận
Bước 1: Xác định công thức hàm số của đại lượng cần xét (hoặc đề bài đưa ra).
Bước 2: Tìm đường tiệm cận của đồ thị hàm số phù hợp với yêu cầu đề bài để tìm kết quả.
Lưu ý: Thường các bài toán cần xác định con số “tối đa” theo ẩn t (thời gian), ta tìm tiệm cận ngang của đồ thị hàm số khi x tiến tới vô cực, hay \(\mathop {\lim }\limits_{x \to + \infty } y\).
Ví dụ minh hoạ:
1) Một bể chứa 6000 lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ 25 gam muối cho mỗi lít nước với tốc độ 20 lít/phút. Giả sử sau t phút, tỉ số giữa khối lượng muối trong bể và thể tích nước trong bể (đơn vị: gam/lít) là một hàm f(t). Xác định hàm số f(t), \(t \in [0; + \infty )\). Nồng độ muối tối đa có trong bể bằng bao nhiêu?
Giải:
Sau t phút khối lượng muối trong bể là 25.20t = 500t (gam).
Thể tích nước trong bể sau t phút là 6000 + 20t (lít).
Khi đó \(f(t) = \frac{{500t}}{{6000 + 20t}} = \frac{{25t}}{{3000 + t}}\) (gam/lít), \(t \in [0; + \infty )\).
\(\mathop {\lim }\limits_{x \to + \infty } f(t) = \mathop {\lim }\limits_{x \to + \infty } \frac{{25t}}{{3000 + t}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{25}}{{\frac{{3000}}{t} + 1}} = 25\).
Vậy nồng độ muối tối đa trong bể là 25 (gam/lít).
2) Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số \(N\left( t \right) = \frac{{25t + 10}}{{t + 5}},t \ge 0\), trong đó N(t) được tính bằng nghìn người. Tính đạo hàm N’(t) và \(\mathop {\lim }\limits_{t \to + \infty } N\left( t \right)\). Từ đó giải thích tại sao dân số của thị trấn đó luôn tăng nhưng sẽ không vượt qua một ngưỡng nào đó.
Giải:
Ta có: \(\mathop {\lim }\limits_{t \to + \infty } N\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } \frac{{25t + 10}}{{t + 5}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{25 + \frac{{10}}{t}}}{{1 + \frac{5}{t}}} = 25\).
\(N'(t) = \left[ {\frac{{25t + 10}}{{t + 5}}} \right]' = \frac{{(25t + 10)'(t + 5) - (25t + 10)(t + 5)'}}{{{{(t + 5)}^2}}}\)
\( = \frac{{25(t + 5) - (25t + 10)}}{{{{(t + 5)}^2}}} = \frac{{115}}{{{{(t + 5)}^2}}} > 0\) \(\forall t \in D\).
Vì \(\mathop {\lim }\limits_{t \to + \infty } N\left( t \right) = 25\) và \(N'(t) > 0\) nên dân số của thị trấn đó luôn tăng nhưng sẽ không vượt qua ngưỡng 25 nghìn người.

 Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan ..
Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan .. 






Danh sách bình luận