Cách biện luận theo m số nghiệm của phương trình dựa vào đồ thị - Toán 12

Giao điểm của đồ thị hàm số y = f(x) và y = g(x) có toạ độ là nghiệm của hệ phương trình y = f(x) và y = g(x).

Phương trình hoành độ giao điểm: f(x) = g(x) (1)

Tương giao đồ thị hàm số chính là số giao điểm của 2 đồ thị hay số nghiệm của phương trình (1).

Cho phương trình (*) chứa f(x) và đồ thị hàm số y = f(x).

Bước 1: Cô lập f(x) từ phương trình đề bài cho, ta được f(x) = g(x).

Bước 2: Số giao điểm của đồ thị hàm số y = f(x) và y = g(x) chính là số nghiệm của (*).

Ví dụ minh hoạ:

1) Cho hàm số \(y =  - {x^4} + 2{x^2}\) có đồ thị như hình dưới.

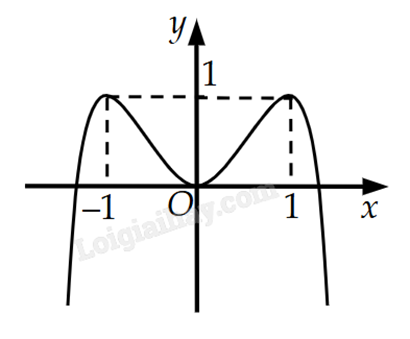
Tất cả các giá trị thực của tham số m để phương trình \( - {x^4} + 2{x^2} = m\) có bốn nghiệm thực phân biệt là

A. \(m > 0\)

B. \(0 \le m \le 1\)

C. \(0 < m < 1\)

D. \(m < 1\)

Giải:

Phương trình \( - {x^4} + 2{x^2} = m\) có bốn nghiệm thực phân biệt khi và chỉ khi đồ thị hàm số \(y =  - {x^4} + 2{x^2}\) cắt đường thẳng y = m tại bốn điểm phân biệt.

Khi đó, đường thẳng y = m phải nằm trên trục hoành y = 0 và nằm dưới đường thẳng y = 1 để cắt đồ thị hàm số \(y =  - {x^4} + 2{x^2}\) tại bốn điểm phân biệt.

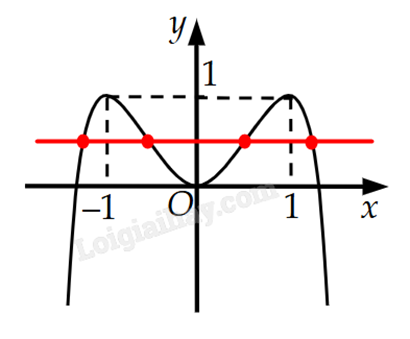
Do đó, 0 < m < 1. Đáp án cần chọn là C.

2) Cho hàm số \(y = {x^3} - 3{x^2} + 1\) có đồ thị như hình dưới.

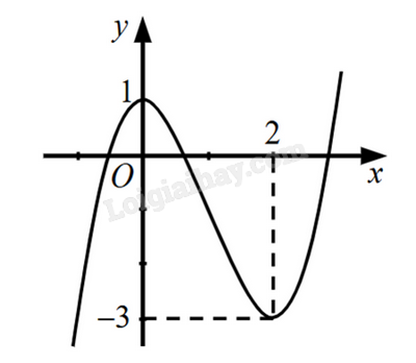
Tất cả các giá trị thực của tham số m để phương trình \({x^3} - 3{x^2} - m = 0\) có hai nghiệm thực phân biệt là

A. (-3;1)

B. {-3;1}

C. (-4;0)

D. {-4;0}

Giải:

Ta có \({x^3} - 3{x^2} - m = 0 \Leftrightarrow {x^3} - 3{x^2} = m \Leftrightarrow {x^3} - 3{x^2} + 1 = m + 1\).

Phương trình \({x^3} - 3{x^2} - m = 0\) có hai nghiệm thực phân biệt khi và chỉ khi đồ thị hàm số \(y = {x^3} - 3{x^2} + 1\) cắt đường thẳng y = m + 1 tại hai điểm phân biệt.

Khi đó, đường thẳng y = m + 1 phải trùng với đường thẳng y = -3 hoặc đường thẳng y = 1 để đồ thị hàm số \(y = {x^3} - 3{x^2} + 1\) cắt đường thẳng y = m + 1 tại hai điểm phân biệt.

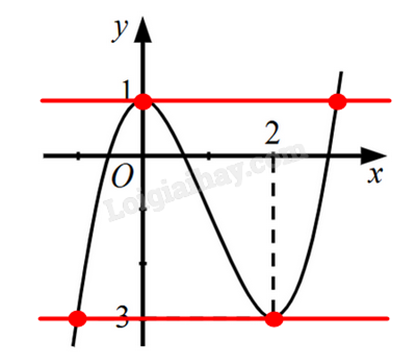
TH1: y = m + 1 trùng với y = 1 \( \Leftrightarrow m + 1 = 1 \Leftrightarrow m = 0\).

TH2: y = m + 1 trùng với y = -3 \( \Leftrightarrow m + 1 =  - 3 \Leftrightarrow m =  - 4\).

Vậy đáp án cần chọn là D.