Cách biện luận theo m số nghiệm của phương trình chứa dấu giá trị tuyệt đối - Toán 12

Giao điểm của đồ thị hàm số y = f(x) và y = g(x) có toạ độ là nghiệm của hệ phương trình y = f(x) và y = g(x).

Phương trình hoành độ giao điểm: f(x) = g(x) (1)

Tương giao đồ thị hàm số chính là số giao điểm của 2 đồ thị hay số nghiệm của phương trình (1).

Bước 1: Vẽ lại đồ thị y = |f(x)| từ đồ thị y = f(x).

- Giữ nguyên phần đồ thị phía trên trục Ox.

- Lấy đối xứng phần đồ thị phía dưới trục Ox qua Ox.

- Xoá phần đồ thị phía dưới Ox.

Bước 2: Số giao điểm của đồ thị hàm số y = |f(x)| và y = m chính là số nghiệm của phương trình |f(x)| = m.

Ví dụ minh hoạ:

Biết đường cong trong hình dưới là đồ thị của hàm số \(y =  - {x^3} + 3x + 2\). Tập hợp tất cả các giả trị của tham số thực m để phương trình \(\left| { - {x^3} + 3x + 2} \right| = m\) có bốn nghiệm phân biệt là?

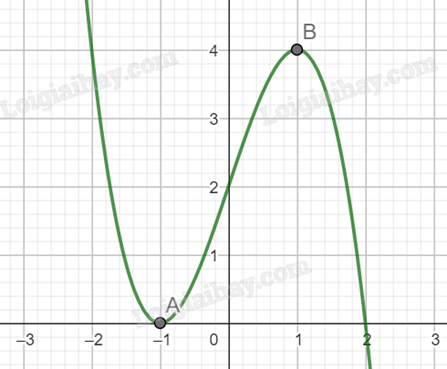
Giải:

Vẽ lại đồ thị hàm số \(y = \left| { - {x^3} + 3x + 2} \right|\):

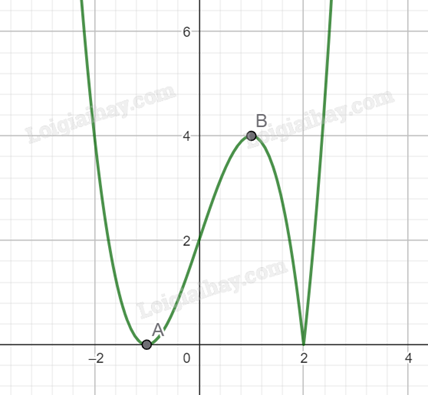
Để phương trình \(\left| { - {x^3} + 3x + 2} \right| = m\) có bốn nghiệm phân biệt thì đồ thị hàm số \(y = \left| { - {x^3} + 3x + 2} \right|\) cắt đường thẳng y = m tại bốn điểm phân biệt.

Khi đó, đường thẳng y = m phải nằm trên trục hoành y = 0 và nằm dưới đường thẳng y = 4.

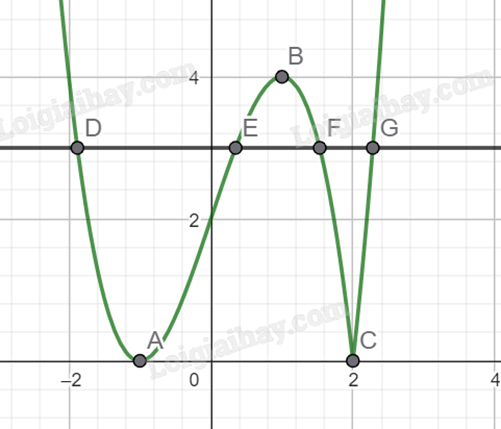
Vậy, tập hợp tất cả các giả trị của tham số thực m để phương trình \(\left| { - {x^3} + 3x + 2} \right| = m\) có bốn nghiệm phân biệt là (0;4).

Bước 1: Vẽ lại đồ thị y = f(|x|) từ đồ thị y = f(x).

- Giữ nguyên phần đồ thị bên phải trục Oy.

- Xoá phần đồ thị bên trái trục Oy.

- Lấy đối xứng phần đồ thị bên phải trục Oy qua Oy.

Bước 2: Số giao điểm của đồ thị hàm số y = |f(x)| và y = m chính là số nghiệm của phương trình |f(x)| = m.

Ví dụ minh hoạ:

Biết đường cong trong hình dưới là đồ thị của hàm số \(y =  - {x^3} + 3x + 2\). Tập hợp tất cả các giả trị của tham số thực m để phương trình \( - {\left| x \right|^3} + 3\left| x \right| + 2 = m\) có bốn nghiệm phân biệt là?

Bước 1: Vẽ lại đồ thị y = f(|x|) từ đồ thị y = f(x).

- Giữ nguyên phần đồ thị bên phải trục Oy.

- Xoá phần đồ thị bên trái trục Oy.

- Lấy đối xứng phần đồ thị bên phải trục Oy qua Oy.

Bước 2: Số giao điểm của đồ thị hàm số y = |f(x)| và y = m chính là số nghiệm của phương trình |f(x)| = m.

Ví dụ minh hoạ:

Biết đường cong trong hình dưới là đồ thị của hàm số \(y =  - {x^3} + 3x + 2\). Tập hợp tất cả các giả trị của tham số thực m để phương trình \( - {\left| x \right|^3} + 3\left| x \right| + 2 = m\) có bốn nghiệm phân biệt là?

Bước 1: Vẽ lại đồ thị y = f(|x|) từ đồ thị y = f(x).

- Giữ nguyên phần đồ thị bên phải trục Oy.

- Xoá phần đồ thị bên trái trục Oy.

- Lấy đối xứng phần đồ thị bên phải trục Oy qua Oy.

Bước 2: Số giao điểm của đồ thị hàm số y = |f(x)| và y = m chính là số nghiệm của phương trình |f(x)| = m.

Ví dụ minh hoạ:

Biết đường cong trong hình dưới là đồ thị của hàm số \(y =  - {x^3} + 3x + 2\). Tập hợp tất cả các giả trị của tham số thực m để phương trình \( - {\left| x \right|^3} + 3\left| x \right| + 2 = m\) có bốn nghiệm phân biệt là?

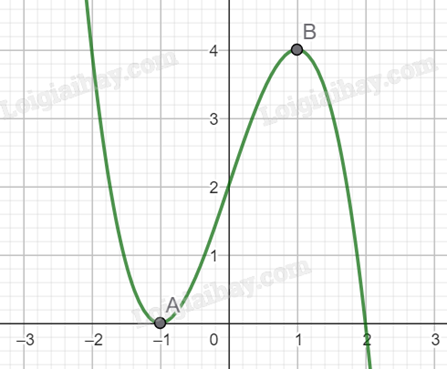
Giải:

Vẽ lại đồ thị hàm số \(y =  - {\left| x \right|^3} + 3\left| x \right| + 2\):

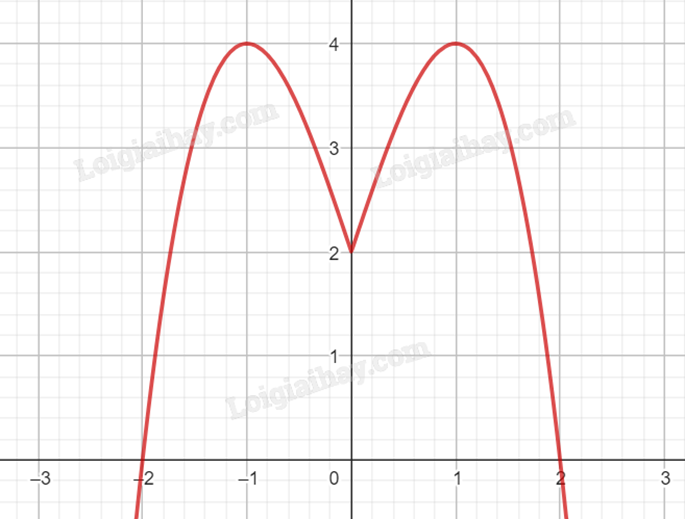
Để phương trình  có bốn nghiệm phân biệt thì đồ thị hàm số \(y =  - {\left| x \right|^3} + 3\left| x \right| + 2\) cắt đường thẳng y = m tại bốn điểm phân biệt.

Khi đó, đường thẳng y = m phải nằm trên đường thẳng y = 2 và nằm dưới đường thẳng y = 4.

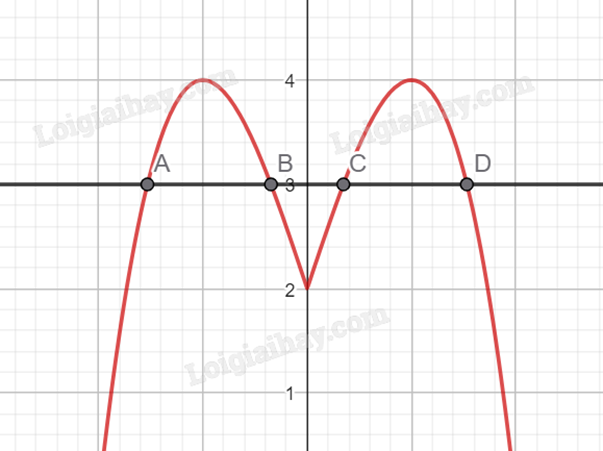
Vậy, tập hợp tất cả các giá trị của tham số thực m để phương trình \(\left| { - {x^3} + 3x + 2} \right| = m\) có bốn nghiệm phân biệt là (0;4).