1. Góc giữa hai vecto là gì?
Trong không gian, cho hai vecto \(\overrightarrow a ,\overrightarrow b \ne \overrightarrow 0 \). Lấy một điểm O bất kì và gọi A, B là hai điểm sao cho \(\overrightarrow {OA} = \overrightarrow a \), \(\overrightarrow {OB} = \overrightarrow b \). Khi đó, \(\widehat {AOB}\) \(\left( {{0^o} < \widehat {AOB} < {{180}^o}} \right)\) được gọi là góc giữa hai vecto \(\overrightarrow a \) và \(\overrightarrow b \), kí hiệu là \(\left( {\overrightarrow a ,\overrightarrow b } \right)\).
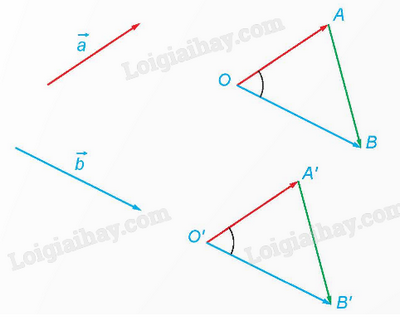
2. Cách xác định góc giữa hai vecto trong không gian
- Góc giữa hai vecto chung điểm đầu trong không gian:
Để tính góc giữa hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \), ta tính số đo \(\widehat {BAC}\).
- Góc giữa hai vecto không có chung điểm đầu trong không gian:
Giả sử cần tính góc giữa \(\overrightarrow a \) và \(\overrightarrow b \) không chung điểm đầu. Ta tìm hai vecto cùng hướng với \(\overrightarrow a \) và \(\overrightarrow b \), có chung điểm đầu; sau đó tính góc giữa hai vecto vừa tìm. Một trong hai vecto vừa tìm có thể là chính \(\overrightarrow a \) hoặc \(\overrightarrow b \).
* Lưu ý:
- Góc giữa hai vecto nhận giá trị từ \({0^o}\) đến \({180^o}\).
- Góc giữa hai vecto cùng hướng bằng \({0^o}\), góc giữa hai vecto ngược hướng bằng \({180^o}\).
- Nếu góc giữa \(\overrightarrow a \) và \(\overrightarrow b \) bằng \(\alpha \) thì góc giữa \(\overrightarrow a \) và \( - \overrightarrow b \) bằng \({180^o} - \alpha \).
- Góc giữa \(\overrightarrow a \) và \(\overrightarrow b \) còn được kí hiệu là \(\left( {\overrightarrow a ,\overrightarrow b } \right)\).
Ví dụ minh hoạ:
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Góc giữa \(\overrightarrow {AC} \) và \(\overrightarrow {DA'} \) bằng bao nhiêu độ?
Giải:
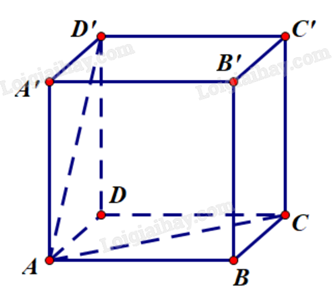
Ta có: \(\left( {\overrightarrow {AC} ,\overrightarrow {DA'} } \right)\)
\( = \left( {\overrightarrow {A'C'} ,\overrightarrow {DA'} } \right)\) (vì \(\overrightarrow {AC} \) cùng hướng với \(\overrightarrow {A'C'} \))
\( = {180^o} - \left( {\overrightarrow {A'C'} ,\overrightarrow {A'D} } \right)\) (vì \(\overrightarrow {A'D} = - \overrightarrow {DA'} \))
\( = {180^o} - \widehat {DA'C}\)
\( = {180^o} - {60^o}\) (vì \(\Delta DA'C\) đều, do \(DA' = A'C' = C'D = a\sqrt 2 \))
\( = {30^o}\).
Vậy góc giữa \(\overrightarrow {AC} \) và \(\overrightarrow {DA'} \) bằng \({30^o}\).
3. Cách tính góc giữa hai vecto trong không gian ứng dụng tích có hướng
Để tính góc giữa hai vecto \(\overrightarrow a \) và \(\overrightarrow b \), ta áp dụng công thức:
\(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\).

 Vecto trong không gian - Từ điển môn Toán 12
Vecto trong không gian - Từ điển môn Toán 12 






Danh sách bình luận