Tích vô hướng là gì? Cách tính tích vô hướng của hai vecto trong không gian - Toán 12

Trong không gian, cho hai vecto \(\overrightarrow a ,\overrightarrow b  \ne \overrightarrow 0 \). Tích vô hướng của hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) là một số, kí hiệu là \(\overrightarrow a .\overrightarrow b \).

Để tính tích vô hướng của hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) trong không gian, ta áp dụng công thức:

\(\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).

Vi dụ minh hoạ:

Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính:

a) \(\overrightarrow {BC} .\overrightarrow {AH} \);

b) \(\overrightarrow {AF} .\overrightarrow {EG} \);

c) \(\overrightarrow {AC} .\overrightarrow {FE} \).

Giải:

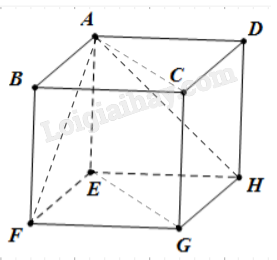
Giả sử hình lập phương ABCD.EFGH có cạnh a.

a) Tính \(\overrightarrow {BC} {\rm{\;}}{\rm{.}}\overrightarrow {AH} \):

+ \(\left| {\overrightarrow {BC} } \right| = a\).

+ \(\left| {\overrightarrow {AH} } \right| = \sqrt {{a^2} + {a^2}}  = a\sqrt 2 \).

+ Góc giữa \(\overrightarrow {BC} \) và \(\overrightarrow {AH} \) là \({45^o}\) vì \(\overrightarrow {BC} {\rm{\;}} = \overrightarrow {AD} \) mà \(\left( {\overrightarrow {AD} ,\overrightarrow {AH} } \right) = {45^o}\).

Do đó: \(\overrightarrow {BC} {\rm{\;}}{\rm{.}}\overrightarrow {AH} {\rm{\;}} = \left| {\overrightarrow {BC} } \right|.\left| {\overrightarrow {AH} } \right|.\cos {45^o} = a.a\sqrt 2 {\rm{\;}}{\rm{.}}\frac{1}{{\sqrt 2 }} = {a^2}\).

b) Tính \(\overrightarrow {AF} {\rm{\;}}{\rm{.}}\overrightarrow {EG} \):

- \(\left| {\overrightarrow {AF} } \right| = a\sqrt 2 \).

- \(\left| {\overrightarrow {EG} } \right| = a\sqrt 2 \).

- Góc giữa \(\overrightarrow {AF} \) và \(\overrightarrow {EG} \) là \({60^o}\) vì \(\overrightarrow {EG} {\rm{\;}} = \overrightarrow {AC} \) mà tam giác ACF đều.

Do đó: \(\overrightarrow {AF} {\rm{\;}}{\rm{.}}\overrightarrow {EG} {\rm{\;}} = \left| {\overrightarrow {AF} } \right|.\left| {\overrightarrow {EG} } \right|.\cos {60^o} = a\sqrt 2 {\rm{\;}}{\rm{.}}a\sqrt 2 {\rm{\;}}{\rm{.}}\frac{1}{2} = {a^2}\).

c) Tính \(\overrightarrow {AC} {\rm{\;}}{\rm{.}}\overrightarrow {FE} \):

- \(\left| {\overrightarrow {AC} } \right| = a\sqrt 2 \).

- \(\left| {\overrightarrow {FE} } \right| = a\).

- Góc giữa \(\overrightarrow {AC} \) và \(\overrightarrow {FE} \) là \({135^o}\) vì góc giữa \(\overrightarrow {AC} \) và vectơ đối của \(\overrightarrow {FE} \) là \(\overrightarrow {EF} \) là \({45^o}\) mà \(\left( {\overrightarrow {AC} ,\overrightarrow {EF} } \right) + \left( {\overrightarrow {AC} ,\overrightarrow {FE} } \right) = {180^o}\).

Do đó: \(\overrightarrow {AC} {\rm{\;}}{\rm{.}}\overrightarrow {FE} {\rm{\;}} = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {FE} } \right|.\cos {135^o} = a\sqrt 2 {\rm{\;}}{\rm{.}}a.\cos {135^o} = a\sqrt 2 {\rm{\;}} \cdot a \cdot \left( { - \frac{1}{{\sqrt 2 }}} \right) = {\rm{\;}} - {a^2}\).

Để tính góc giữa hai vecto \(\overrightarrow a \) và \(\overrightarrow b \), ta áp dụng công thức:

\(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\).