Hệ trục toạ độ. Cách tìm toạ độ điểm và vecto trong không gian - Toán 12

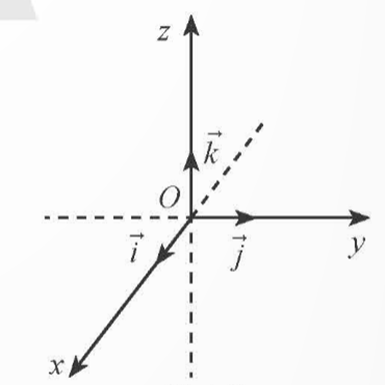
Trong không gian, ba trục Ox, Oy, Oz đôi một vuông góc với nhau tại gốc O của mỗi trục. Gọi \(\overrightarrow i \), \(\overrightarrow j \), \(\overrightarrow k \) là các vecto đơn vị trên các trục Ox, Oy, Oz.

- Hệ ba trục như vậy gọi là hệ trục toạ độ Descartes vuông góc Oxyz, hay đơn giản là hệ toạ độ Oxyz.

- Điểm O được gọi là gốc toạ độ.

- Các mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau được gọi là các mặt phẳng toạ độ.

Không gian với hệ toạ độ Oxyz còn được gọi là không gian Oxyz.

Vì \(\overrightarrow i \), \(\overrightarrow j \), \(\overrightarrow k \) là các vecto đơn vị đôi một vuông góc với nhau nên ta có:

\({\overrightarrow i ^2} = {\overrightarrow j ^2} = {\overrightarrow k ^2}\) và \(\overrightarrow i .\overrightarrow j  = \overrightarrow j .\overrightarrow k  = \overrightarrow k .\overrightarrow i  = 0\).

* Toạ độ của điểm: \(M\left( {x;y;z} \right) \Leftrightarrow \overrightarrow {OM}  = x\overrightarrow i  + y\overrightarrow j  + z\overrightarrow k \).

* Toạ độ của vecto: \(\overrightarrow a \left( {x;y;z} \right) \Leftrightarrow \overrightarrow a  = x\overrightarrow i  + y\overrightarrow j  + z\overrightarrow k \).

Với hai điểm \(A\left( {{x_A};{y_A};{z_A}} \right)\) và \(B\left( {{x_B};{y_B};{z_B}} \right)\), ta có \(\overrightarrow {AB}  = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\).

Ví dụ minh hoạ:

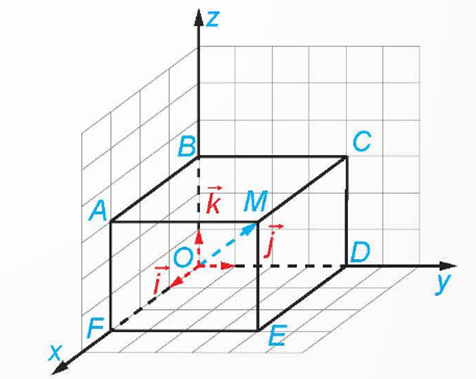
1) Hình dưới minh hoạ một hệ toạ độ Oxyz trong không gian cùng với các hình vuông có cạnh bằng 1 đơn vị. Tìm toạ độ của điểm M.

Giải:

Áp dụng quy tắc hình hộp, ta có \(\overrightarrow {OM}  = \overrightarrow {OF}  + \overrightarrow {OD}  + \overrightarrow {OB}  = 3\overrightarrow i  + 4\overrightarrow j  + 3\overrightarrow z \).

Vậy, toạ độ điểm M là (3;4;3).

2) Không gian với trục hệ toạ độ Oxyz, cho \(\vec a= 2\vec j- \vec i+ 3\vec k.\) Toạ độ của vecto \(\vec a\) là gì?

Giải:

\(\vec a= - \vec i+ 2\vec j+ 3\vec k= \left( { - 1;2;3} \right)\).

3) Trong không gian Oxy, cho hai điểm A(-2;1;0), B(3;-2;1). Toạ độ của vecto \(\overrightarrow {AB} \) là gì?

Giải:

\(\overrightarrow {AB} = (3 + 2; - 2 - 1;1 - 0) = (5; - 3;1)\).