Vecto trong không gian - Từ điển môn Toán 12 
1. Vecto cùng phương là gì?
Hai vecto được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
Nếu \(\overrightarrow a \) cùng phương với \(\overrightarrow b \) thì \(\overrightarrow a = k\overrightarrow b \).
2. Cách chứng minh ba điểm thẳng hàng dựa vào vecto cùng phương trong không gian
Để chứng minh ba điểm A, B, C bất kì thẳng hàng, ta tìm số thực k khác 0 sao cho \(\overrightarrow {AB} = k\overrightarrow {AC} \).
Ví dụ minh hoạ:
Cho tam giác ABC, trung tuyến AD. Gọi M là trung điểm của AD, điểm N thuộc AC sao cho \(\overrightarrow {AC} = 3\overrightarrow {AN} \). Chứng minh B, M, N thẳng hàng.
Giải:
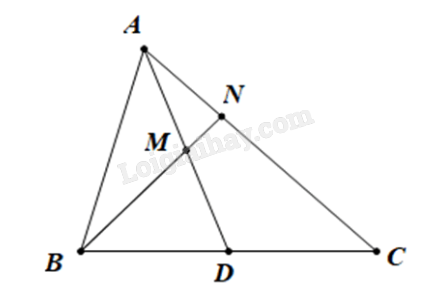
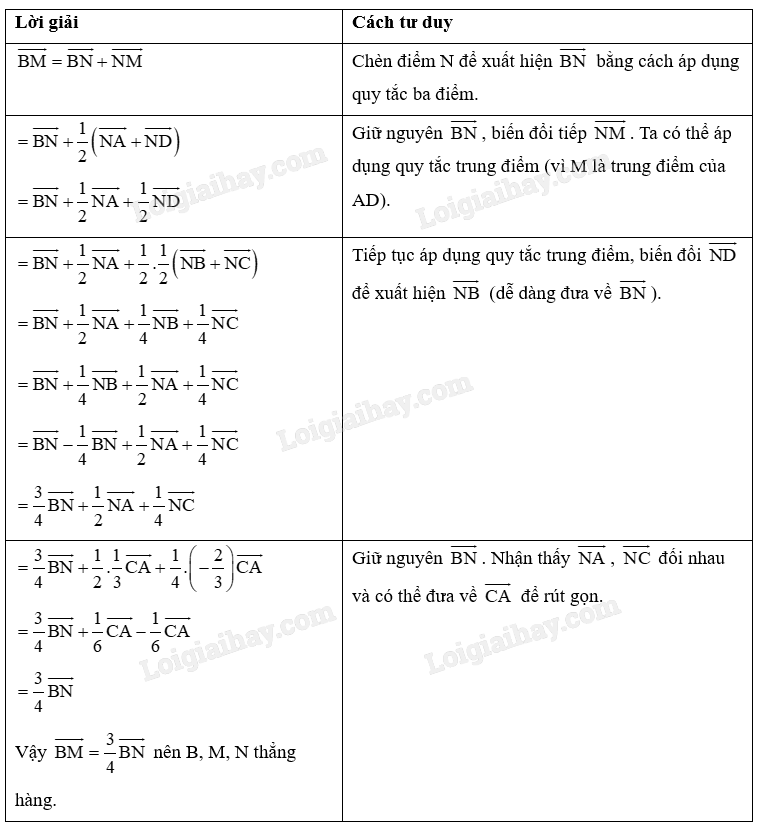
Ta cần chứng minh \(\overrightarrow {BM} = k\overrightarrow {BN} \), hay biến đổi \(\overrightarrow {BM} \) về \(\overrightarrow {BN} \).
