Tương giao đồ thị - Từ điển môn Toán 12 1. Tương giao đồ thị hàm số là gì?
Giao điểm của đồ thị hàm số y = f(x) và y = g(x) có toạ độ là nghiệm của hệ phương trình y = f(x) và y = g(x).
Phương trình hoành độ giao điểm: f(x) = g(x) (1)
Tương giao đồ thị hàm số chính là số giao điểm của 2 đồ thị hay số nghiệm của phương trình (1).
2. Cách tìm số nghiệm của phương trình dựa vào đồ thị hàm số
Cho phương trình (*) chứa f(x) và đồ thị hàm số y = f(x).
Bước 1: Cô lập f(x) từ phương trình đề bài cho, ta được f(x) = g(x).
Bước 2: Số giao điểm của đồ thị hàm số y = f(x) và y = g(x) chính là số nghiệm của (*).
Ví dụ minh hoạ:
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình dưới. Phương trình 3f(x) + 4 = 0 có tất cả bao nhiêu nghiệm?
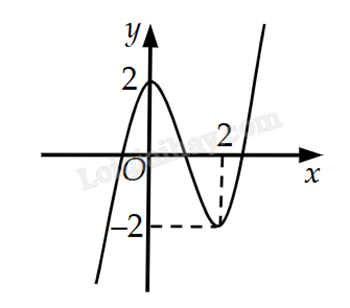
Giải:
\(3f(x) - 4 = 0 \Leftrightarrow f(x) = \frac{4}{3}\).
Vì \( - 2 < \frac{4}{3} < 2\) nên ta vẽ đường thẳng \(y = \frac{4}{3}\) như sau:
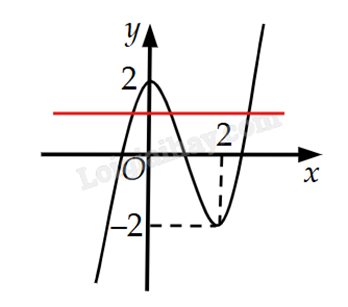
Thấy đường thẳng \(y = \frac{4}{3}\) cắt đồ thị y = f(x) tại ba điểm nên phương trình 3f(x) – 4 = 0 có ba nghiệm.
3. Cách tìm số nghiệm của phương trình dựa vào bảng biến thiên
Cho phương trình (*) chứa f(x) và bảng biến thiên của hàm số y = f(x).
Bước 1: Cô lập f(x) từ phương trình đề bài cho, ta được f(x) = g(x).
Bước 2: Số giao điểm của đồ thị hàm số y = f(x) và y = g(x) chính là số nghiệm của (*).
Ví dụ minh hoạ:
Cho hàm số f = f(x) có bảng biến thiên như hình dưới. Phương trình f(x) – 2 = 0 có bao nhiêu nghiệm?
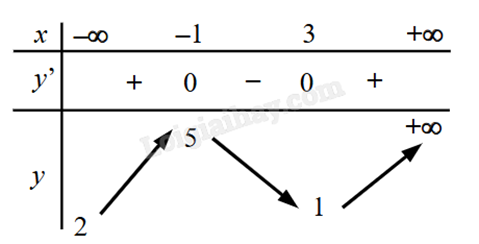
\(f(x) - 2 = 0 \Leftrightarrow f(x) = 2\).
Vì 1 < 2 < 5 nên ta biểu diễn đường thẳng y = 2 trên bảng biến thiên như sau:
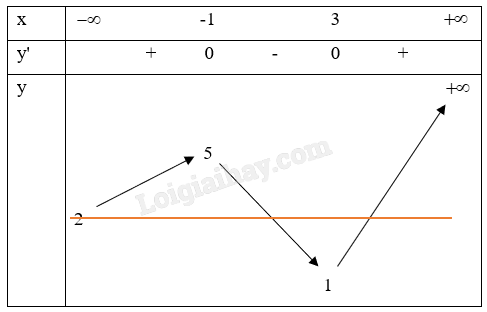
Vì \(\mathop {\lim }\limits_{x \to - \infty } f(x) = 2\) nên y = 2 là đường tiệm cận ngang của đồ thị hàm số. Do đó, ta loại giao điểm đầu tiên.
Đường thẳng y = 2 cắt đồ thị y = f(x) tại hai điểm nên phương trình f(x) – 2 = 0 có hai nghiệm.
