1. Ứng dụng của đạo hàm
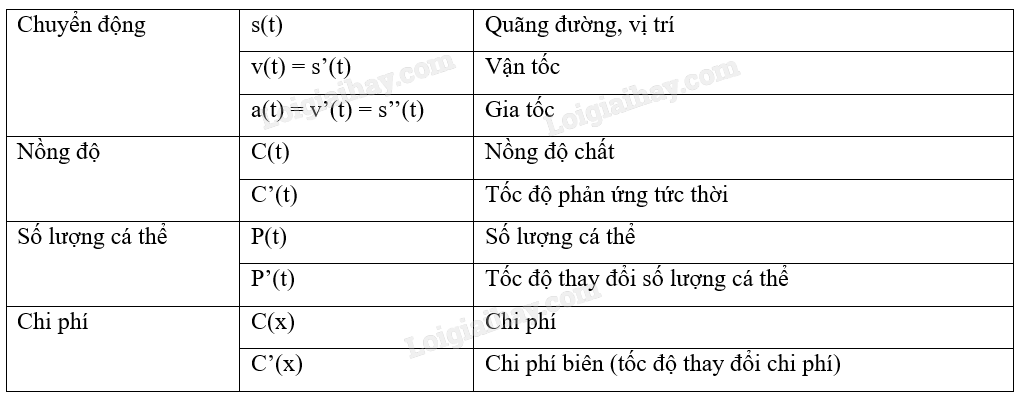
Đạo hàm f’(a) là tốc độ thay đổi tức thời của đại lượng y = f(x) đối với x tại điểm x = a. Ta xét một số ứng dụng của ý tưởng này đối với vật lý, hoá học và kinh tế.
2. Cách giải bài toán về tốc độ thay đổi của một đại lượng ứng dụng đạo hàm
Ví dụ minh hoạ:
1) Một chất điểm chuyển động theo phương trình \(s(t) = \frac{1}{3}{t^3} + 18{t^2} - 35t + 10\), trong đó t tính bằng giây, s tính bằng mét. Trong 40 giây đầu tiên, chất điểm đó có vận tốc tức thời giảm trong khoảng thời gian (a;b). Tính giá trị biểu thức P = a + 9b.
Giải:
1) \(v(t) = s'(t) = - {t^2} + 36t - 35\).
\(v'(t) = - 2t + 36 = 0 \Leftrightarrow t = 18\).

Từ bảng biến thiên, ta thấy trong khoảng (18;40) giây, vận tốc tức thời của chất điểm giảm.
P = 18 + 9.40 = 378.
2) Giả sử số lượng của một quần thể nấm X tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hoá bằng hàm số \(P(t) = 120{e^{0,15t}}\), trong đó thời gian t được tính bằng giờ. Tại thời điểm ban đầu t = 0, tốc độ tăng trưởng của quần thể nấm X là bao nhiêu (đơn vị: tế bào/giờ)?
Giải:
Hàm tốc độ tăng trưởng của quần thể nấm là \(P'(t) = 120.0,15.{e^{0,15t}} = 18.{e^{0,15t}}\) (tế bào/giờ).
Tốc độ tăng trưởng của quần thể nấm ở thời điểm t = 0 là \(P'(0) = 18.{e^{0,15.0}} = 18.{e^0} = 18\) (tế bào/giờ).
3. Cách giải bài toán tối ưu ứng dụng đạo hàm
Bước 1: Đặt ẩn, lập phương trình biểu diễn đại lượng cần tính giá trị lớn nhất hoặc giá trị nhỏ nhất (nếu đề bài chưa cho sẵn).
Bước 2: Tính đạo hàm. Lập bảng biến thiên và kết luận.
Ví dụ minh hoạ:
1) Một tập chí được bán với giá 20 nghìn đồng một cuốn. Chi phí xuất bản x cuốn tập chí (bao gồm: lương cán bộ, công nhân viên, giấy in, ...) được cho bởi công thức \(C(x) = 0,0001{x^2} - 0,2x + 10000\), C(x) được tính theo đơn vị vạn đồng. Chi phí phát hành cho mỗi cuốn là 4 nghìn đồng. Giả sử T(x) là tổng chi phí (xuất bản và phát hành) cho x cuốn tạp chí. Tỉ số \(M(x) = \frac{{T(x)}}{x}\) được gọi là chi phí trung bình cho một cuốn tạp chí khi xuất bản x cuốn. Tìm số lượng tạp chí cần xuất bản sao cho chi phí trung bình là thấp nhất.
Giải:
Tổng chi phí cho x cuốn tạp chí là \(T(x) = C(x) + 0,4x = 0,0001{x^2} + 0,2x + 10000\).
Ta có \(M(x) = \frac{{T(x)}}{x} = \frac{{0,0001{x^2} + 0,2x + 10000}}{x} = 0,0001x + \frac{{10000}}{x} + 0,2\), với \(x \in {\mathbb{N}^*}\).
\(M'(x) = 0,0001 - \frac{{10000}}{{{x^2}}} = 0 \Leftrightarrow x = 10000\).
Bảng biến thiên:
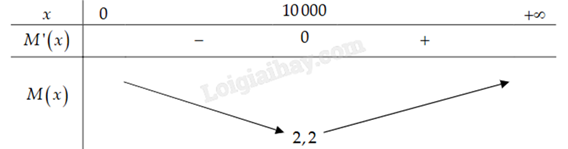
Từ bảng biến thiên, ta thấy chi phí trung bình cho x cuốn tạp chí thấp nhất khi x = 10000 (cuốn).
2) Một hộp không nắp được làm từ một mảnh các tông theo hình vẽ. Hộp có đáy là một hình vuông cạnh x (cm), chiều cao là h (cm) và thể tích là 4000 \(c{m^3}\). Tìm độ dài cạnh hình vuông x sao cho chiếc hộp làm ra tốn ít bìa các tông nhất.
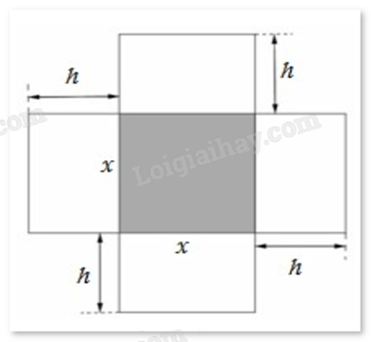
Giải:
Thể tích của hộp là \(V = {x^2}h = 4000\) (\(c{m^3}\)).
Suy ra chiều cao của hộp là \(h = \frac{{4000}}{{{x^2}}}\) (cm).
Diện tích xung quanh của hộp là \(S(x) = {x^2} + 4xh = {x^2} + 4x\frac{{4000}}{{{x^2}}} = {x^2} + \frac{{16000}}{x}\) (\(c{m^2}\)).
Chiếc hộp làm ra tốn ít bìa nhất khi diện tích xung quanh hình hộp nhỏ nhất.
Ta cần tìm giá trị nhỏ nhất của S(x).
Ta có \(S'(x) = 2x - \frac{{16000}}{{{x^2}}} = 0 \Leftrightarrow 2x = \frac{{16000}}{{{x^2}}} \Leftrightarrow 2{x^3} = 16000 \Leftrightarrow {x^3} = 8000 \Leftrightarrow x = 20\).
Ta có bảng biến thiên:
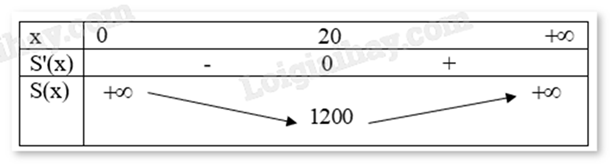
Vậy để tốn ít bìa nhất thì cạnh hình vuông có chiều dài x = 20 (cm).

 Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan ..
Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan .. 






Danh sách bình luận