Cách nhận dạng đồ thị hàm số - Toán 12

Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) \((a,b,c,d \in \mathbb{R},a \ne 0)\).

Đạo hàm: \(y' = 3a{x^2} + 2bx + c\).

Nếu nhánh cuối đồ thị đi lên thì a > 0, nhánh cuối đồ thị đi xuống thì a < 0.

Đồ thị cắt trục tung tại điểm (0;d).

Đồ thị hàm số đi qua điểm \(A\left( {{x_A};{y_A}} \right)\) thì \(f\left( {{x_A}} \right) = {y_A} \Leftrightarrow a{x_A}^3 + b{x_A}^2 + c{x_A} + {d_A} = {y_A}\).

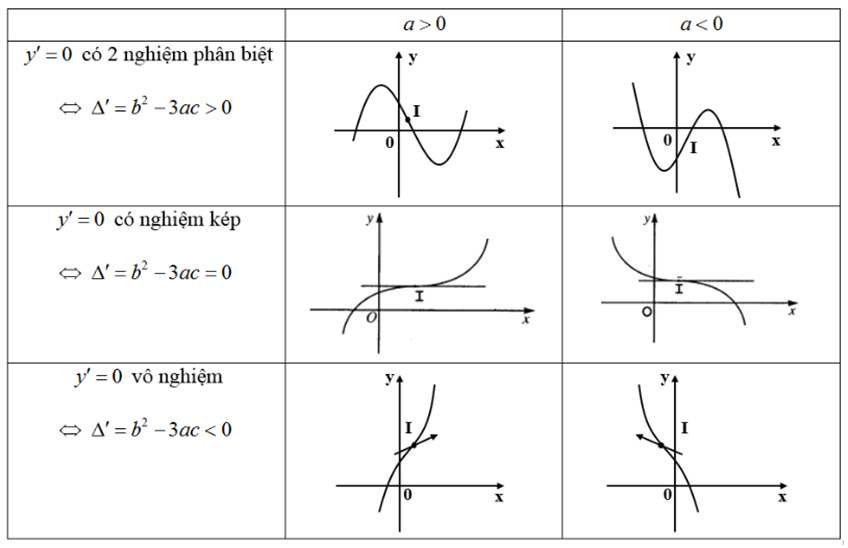
Trường hợp đồ thị có hai điểm cực trị:

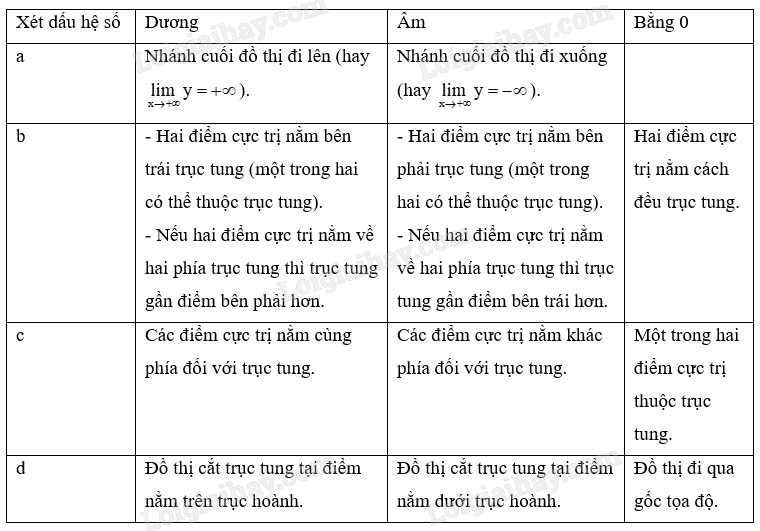
Ví dụ minh hoạ:

Đường cong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?

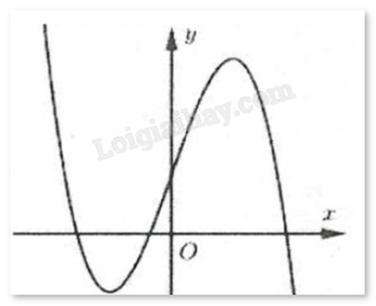
A. \(y =  - {x^3} + 3{x^2} + 1\)

B. \(y =  - {x^3} + 3x + 1\)

C. \(y = {x^3} - 3x + 1\)

D. \(y =  - {x^3} - 3x + 1\)

Giải:

Dựa vào đồ thị ta thấy \(\mathop {\lim }\limits_{x \to  + \infty } y =  - \infty \) nên hệ số a < 0. Loại đáp án C.

Hàm số có hai điểm cực trị \({x_1} < 0 < {x_2}\) nên y’ = 0 có hai nghiệm trái dấu.

Xét đáp án A, có \(y' =  - 3{x^2} + 6x = 0 \Leftrightarrow \) x = 0 hoặc x = 2 (loại).

Xét đáp án D, có \(y' =  - 3{x^2} - 3x < 0\) \((\forall x \in \mathbb{R})\) (loại).

Vậy đáp án B đúng.

Cho đồ thị hàm số \(y = \frac{{ax + b}}{{cx + d}}\) \((c \ne 0,ad - bc \ne 0)\).

Hàm số đồng biến trên tập xác định: ad – bc > 0.

Hàm số nghịch biến trên tập xác định: ad – bc < 0.

Đồ thị hàm số cắt trục Oy tại điểm có tung độ \(y = \frac{b}{d}\).

Đường tiệm cận đứng của đồ thị nằm bên phải trục tung: \(x =  - \frac{d}{c}\).                                                                                                                

Đường tiệm cận ngang của đồ thị nằm phía dưới trục hoành: \(y = \frac{a}{c}\).

Đồ thị hàm số đi qua điểm \(A\left( {{x_A};{y_A}} \right)\) thì \(f\left( {{x_A}} \right) = {y_A} \Leftrightarrow \frac{{a{x_A} + b}}{{c{x_A} + d}} = {y_A}\).

Ví dụ minh hoạ:

Cho hàm số có bảng biến thiên như hình vẽ sau.

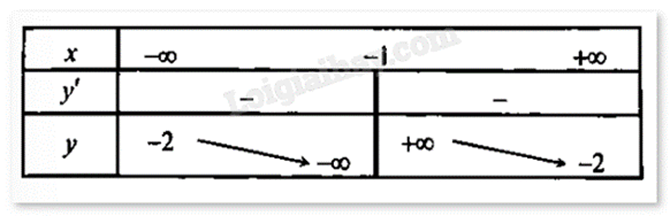
Xác định công thức của hàm số.

A. \(y = \frac{{x - 4}}{{2x + 2}}\)

B. \(y = \frac{{ - 2x - 4}}{{x + 1}}\)

C. \(y = \frac{{ - 2x + 3}}{{x + 1}}\)

D. \(y = \frac{{2 - x}}{{x + 1}}\)

Giải:

Đồ thị hàm số có tiệm cận đứng x = -1 và tiệm cận ngang y = -2. Loại A và D.

Xét hàm số \(y = \frac{{ - 2x - 4}}{{x + 1}}\) có \(y' = \frac{2}{{{{(x + 1)}^2}}} > 0\). Hàm số đồng biến trên các khoảng xác định.

Xét hàm số \(y = \frac{{ - 2x + 3}}{{x + 1}}\) có \(y' = \frac{{ - 5}}{{{{(x + 1)}^2}}} < 0\). Hàm số nghịch biến trên các khoảng xác.

Mà theo bảng biến thiên thì hàm số nghịch biến. Ta chọn hàm số \(y = \frac{{ - 2x + 3}}{{x + 1}}\).