Khái niệm và cách tìm tâm đối xứng của đồ thị hàm số - Toán 12

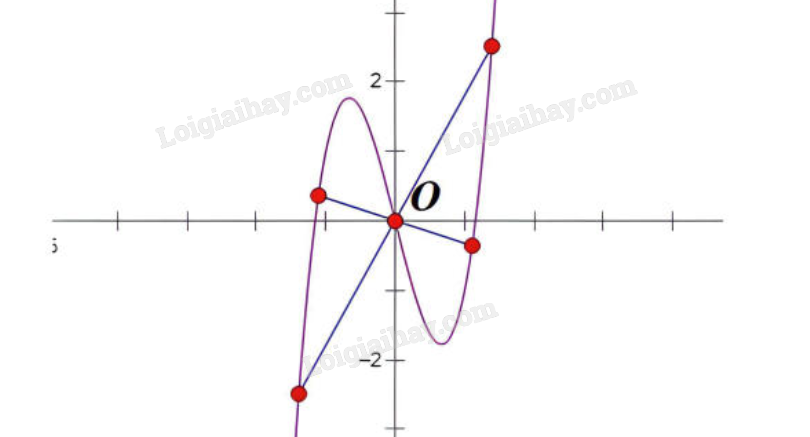
Tâm đối xứng của đồ thị hàm số là một điểm mà khi lấy đối xứng qua điểm đó, mọi điểm trên đồ thị đều có điểm đối xứng cũng nằm trên đồ thị.

1) Hàm đa thức bậc ba \(f(x) = a{x^3} + b{x^2} + cx + d\) \((a \ne 0)\):

Bước 1: Tìm đạo hàm cấp hai f’’(x).

Bước 2: Giải phương trình f’’(x) = 0. Giả sử nghiệm là \({x_0}\).

Bước 3: Kết luận tâm đối xứng có toạ độ \(\left( {{x_0};f({x_0})} \right)\).

2) Hàm phân thức bậc nhất \(f(x) = \frac{{ax + b}}{{cx + d}}\) \((a,c \ne 0)\):

Tâm đối xứng là giao điểm của tiệm cận đứng và tiệm cận ngang.

Đồ thị có tiệm cận đứng \(x = {x_0}\) và tiệm cận ngang \(y = {y_0}\) thì tâm đối xứng có toạ độ \(\left( {{x_0};{y_0}} \right)\).

3) Hàm phân thức bậc hai trên bậc nhất \(f(x) = \frac{{a{x^2} + bx + c}}{{mx + n}}\) \((a,m \ne 0)\):

Tâm đối xứng là giao điểm của tiệm cận đứng và tiệm cận xiên.

Đồ thị có tiệm cận đứng \(x = {x_0}\) và tiệm cận xiên \(y = px + q\) thì tâm đối xứng có toạ độ \(\left( {{x_0};p{x_0} + q} \right)\).

Ví dụ minh hoạ:

a) Hàm số \(y = {x^3} + 3{x^2} - 9x + 1\) có \(y'' = 6x + 6 = 0 \Leftrightarrow x =  - 1\) nên tâm đối xứng của đồ thị là điểm (-1;12).

b) Hàm số \(\frac{{2x + 1}}{{x - 3}}\) có tiệm cận đứng là x = 3, tiệm cận ngang là y = 2. Tâm đối xứng của đồ thị là điểm (3;2).

c) Hàm số \(y = \frac{{{x^2} - 2x + 3}}{{x + 1}}\) có tiệm cận đứng là x = -1, tiệm cận xiên là y = x – 3. Tâm đối xứng của đồ thị là điểm (-1;-4).