1. Đường tiệm cận là gì?
a) Tiệm cận đứng:
Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thoả mãn:
\(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \).
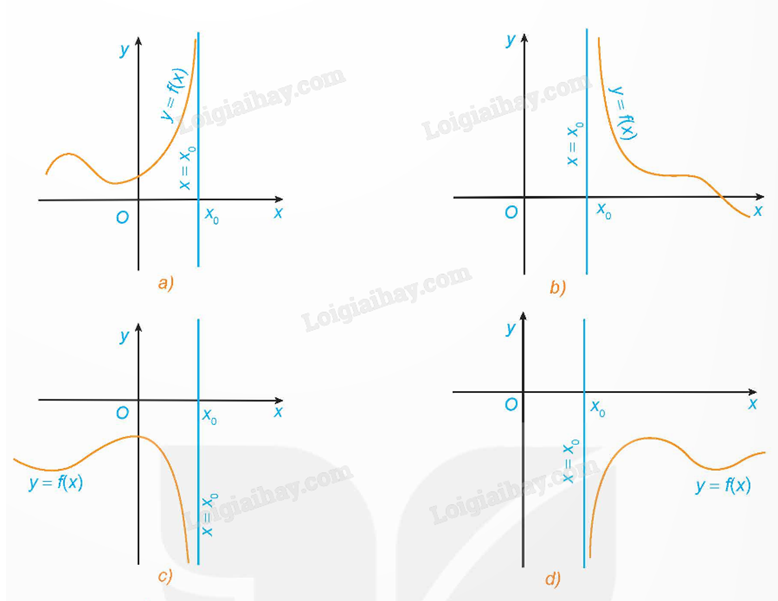
b) Tiệm cận ngang
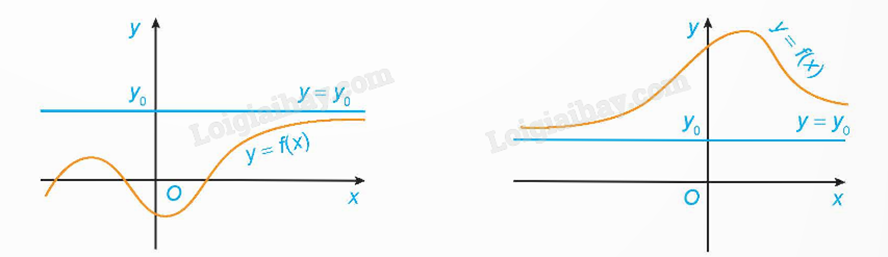
Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu:
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = {y_0}\).
c) Tiệm cận xiên:
Đường thẳng y = ax + b \((a \ne 0)\) gọi là đường tiệm cận xiên của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\).
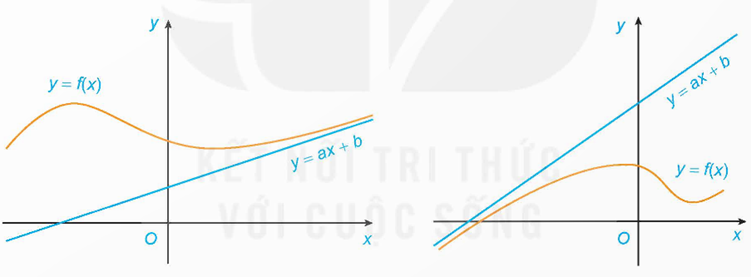
2. Cách tìm đường tiệm cận ngang dựa vào công thức hàm số
Cho hàm số y = f(x).
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Tính \(\mathop {\lim }\limits_{x \to \pm \infty } f(x)\). Nếu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = {y_0}\) thì đồ thị hàm số có tiệm cận ngang là \(y = {y_0}\).
- Đối với hàm phân thức hữu tỉ \(y = \frac{{{a_0}{x^m} + {a_1}{x^{m - 1}} + ... + {a_m}}}{{{b_0}{x^n} + {b_1}{x^{n - 1}} + ... + {b_n}}}\) \(\left( {{a_0} \ne 0,{b_0} \ne 0,m \in {\mathbb{N}^*},n \in {\mathbb{N}^*}} \right)\):
+ Với m = n: Tiệm cận ngang là \(y = \frac{{{a_0}}}{{{b_0}}}\).
+ Với m > n: Không có tiệm cận ngang.
+ Với m < n: Tiệm cận ngang là \(y = 0\).
- Đối với hàm phân thức vô tỉ \(y = \frac{{ax + b}}{{\sqrt {c{x^2} + dx + e} }}\) \(\left( {a \ne 0,c \ne 0} \right)\):
+ Với c < 0: Không có tiệm cận ngang.
+ Với c > 0: Tiệm cận ngang là \(y = \pm \frac{a}{{\sqrt c }}\).
Ví dụ minh hoạ:
1) Tiệm cận ngang của đồ thị hàm số \(\frac{{1 - x}}{{3x + 2}}\) là \(y = - \frac{1}{3}\).
2) Tiệm cận ngang của đồ thị hàm số \(\frac{{3{x^2} + 4}}{{2{x^2} + 1}}\) là \(y = \frac{3}{2}\).
3) Tiệm cận ngang của đồ thị hàm số \(\frac{x}{{{x^2} + 1}}\) là \(y = 0\).
4) Đồ thị hàm số \(\frac{{{x^3} - 1}}{{2{x^2}}}\) không có tiệm cận ngang.
5) Tiệm cận ngang của đồ thị hàm số \(y = \frac{{x + 1}}{{\sqrt {4{x^2} + x + 2} }}\) là \(y = \pm \frac{1}{2}\).
6) Xét hàm số \(y = \frac{{x + \sqrt {4{x^2} - 3} }}{{2x + 3}}\). Ta có:
\(y = \frac{{x + \sqrt {4{x^2} - 3} }}{{2x + 3}} = \frac{{x + \left| x \right|\sqrt {4 - \frac{3}{{{x^2}}}} }}{{2x + 3}} = \frac{x}{{2x + 3}} + \frac{{\left| x \right|\sqrt {4 - \frac{3}{{{x^2}}}} }}{{2x + 3}}\).
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( {\frac{x}{{2x + 3}} + \frac{{\left| x \right|\sqrt {4 - \frac{3}{{{x^2}}}} }}{{2x + 3}}} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\frac{x}{{2x + 3}} + \frac{{x\sqrt {4 - \frac{3}{{{x^2}}}} }}{{2x + 3}}} \right) = \frac{1}{2} + 1 = \frac{3}{2}\).
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{x}{{2x + 3}} + \frac{{\left| x \right|\sqrt {4 - \frac{3}{{{x^2}}}} }}{{2x + 3}}} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{x}{{2x + 3}} + \frac{{ - x\sqrt {4 - \frac{3}{{{x^2}}}} }}{{2x + 3}}} \right) = \frac{1}{2} - 1 = - \frac{1}{2}\).
Vậy tiệm cận ngang của đồ thị hàm số \(y = \frac{{x + \sqrt {4{x^2} - 3} }}{{2x + 3}}\) là \(y = \frac{3}{2}\) và \(y = - \frac{1}{2}\).
3. Cách tìm đường tiệm cận đứng dựa vào công thức hàm số
Cho hàm số y = f(x).
Đường thẳng \(x = {x_0}\) được gọi là tiệm cận đứng của đồ thị hàm số y = f(x) nếu thoả mãn ít nhất một trong các điều kiện:
+ \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty \);
+ \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty \);
+ \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty \);
+ \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \).
Chú ý:
- Đối với các hàm phân thức, \(x = {x_0}\) được gọi là tiệm cận đứng của đồ thị hàm số y = f(x) nếu \({x_0}\) là nghiệm của mẫu thức mà không phải nghiệm của tử thức.
+ Nếu mẫu thức có vô số nghiệm thì đồ thị không có tiệm cận đứng.
+ Nếu tử thức không tồn tại khi \(x = {x_0}\) thì \(x = {x_0}\) không phải tiệm cận đứng.
- Hàm đa thức không có tiệm cận.
Ví dụ minh hoạ:
1) Hàm số \(y = \frac{{x - 1}}{{x + 5}}\) có tiệm cận đứng là x = -5 (nghiệm của mẫu và không là nghiệm của tử).
2) Hàm số \(y = \frac{{2{x^2} + x + 1}}{{{x^2} - 1}}\) có 2 tiệm cận đứng là x = 1 và x = -1 (nghiệm của mẫu và không là nghiệm của tử).
3) Xét hàm số \(y = \frac{1}{{{{\cos }^2}x}}\) có \({\cos ^2}x = 0 \Leftrightarrow \cos x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi \), \(k \in \mathbb{Z}\) nên đồ thị hàm số có vô số đường tiệm cận đứng là các đường thẳng \(x = \frac{\pi }{2} + k\pi \), \(k \in \mathbb{Z}\).
4) Xét hàm số \(y = \frac{1}{{3{{\sin }^2}x + {{\cos }^2}x}}\) có \(3{\sin ^2}x + {\cos ^2}x = 0 \Leftrightarrow 2{\sin ^2}x + 1 = 0\) luôn đúng với mọi x nên đồ thị hàm số này không có tiệm cận.
5) Hàm số \(y = {x^2} + x + 1\) là hàm đa thức nên không có tiệm cận.
6) Xét hàm số \(y = \frac{{\sqrt x }}{{{x^2} - 1}}\):
\(\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty \); \(\mathop {\lim }\limits_{x \to - {1^ + }} y\) và \(\mathop {\lim }\limits_{x \to - {1^ - }} y\) không tồn tại nên đồ thị hàm số đã cho chỉ có tiệm cận đứng là x = 1.
4. Cách tìm đường tiệm cận xiên của đồ thị hàm phân thức bậc hai trên bậc nhất
Cho hàm đa thức \(y = \frac{{a{x^2} + bx + c}}{{dx + e}}\) \(\left( {a \ne 0,d \ne 0} \right)\).
Bước 1: Đưa phân thức \(y = \frac{{a{x^2} + bx + c}}{{dx + e}}\) về dạng \(y = mx + n + \frac{p}{{dx + e}}\) bằng cách chia đa thức \(a{x^2} + bx + c\) cho \(dx + e\), được mx + n là thương và p là phần dư.
Bước 2: Chứng minh \(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {mx + n} \right)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {mx + n} \right)} \right] = 0\).
Bước 3: Kết luận y = mx + n là tiệm cận xiên của đồ thị hàm số.
Ví dụ minh hoạ:
1) Xét hàm số \(y = \frac{{{x^2} - 2x + 3}}{{x + 1}}\) có \(\frac{{{x^2} - 2x + 3}}{{x + 1}} = x - 3 + \frac{6}{{x + 1}}\).
Vì \(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - (x - 3)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{6}{{x + 1}} = 0\) nên y = x – 3 là tiệm cận xiên của đồ thị hàm số.
2) Xét hàm số \(y = \frac{{{x^2} + 2x - 1}}{x}\) có \(\frac{{{x^2} + 2x - 1}}{x} = x + 2 - \frac{1}{x}\).
Vì \(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - (x + 2)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 1}}{x} = 0\) nên y = x + 2 là tiệm cận xiên của đồ thị hàm số.

 Đường tiệm cận của đồ thị hàm số - Từ điển môn Toán 12
Đường tiệm cận của đồ thị hàm số - Từ điển môn Toán 12 






Danh sách bình luận