1. Đường tiệm cận là gì?
a) Tiệm cận đứng:
Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thoả mãn:
\(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \).
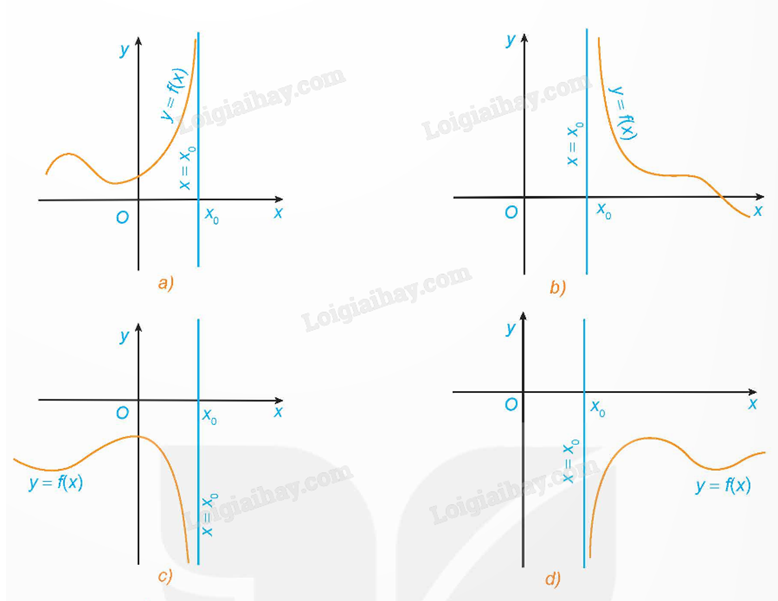
b) Tiệm cận ngang
Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu:
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = {y_0}\).
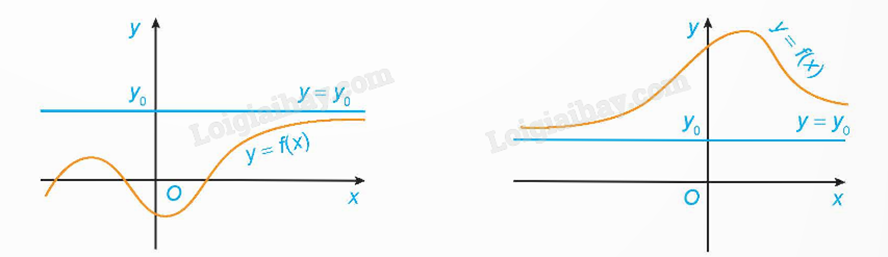
c) Tiệm cận xiên:
Đường thẳng y = ax + b \((a \ne 0)\) gọi là đường tiệm cận xiên của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\).
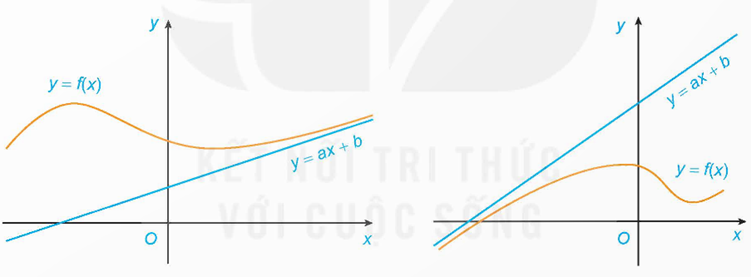
2. Cách tìm đường tiệm cận ngang dựa vào bảng biến thiên
Cho bảng biến thiên của hàm số y = f(x).
Nếu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = {y_0}\) thì đồ thị hàm số có tiệm cận ngang là \(y = {y_0}\).
Ví dụ minh hoạ:
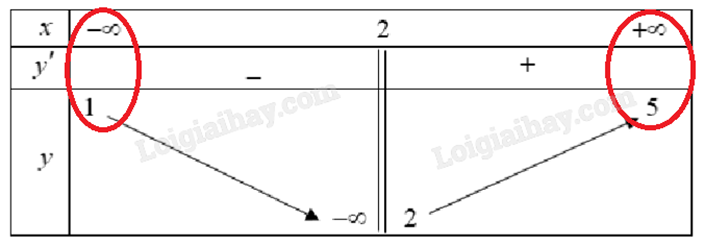
1) Cho bảng biến thiên của hàm số y = f(x):
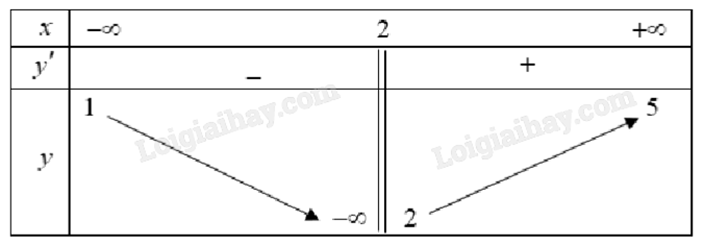
Vì \(\mathop {\lim }\limits_{x \to + \infty } f(x) = 5\) và \(\mathop {\lim }\limits_{x \to - \infty } f(x) = 1\) nên đồ thị hàm số có 2 đường tiệm cận ngang là y = 1 và y = 5.
2) Cho bảng biến thiên của hàm số y = f(x):
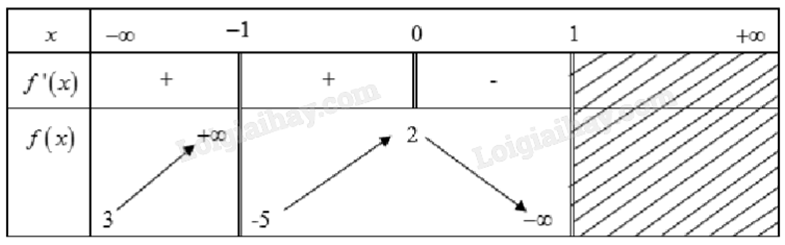
Vì \(\mathop {\lim }\limits_{x \to - \infty } f(x) = 3\) nên đồ thị hàm số có 1 đường tiệm cận ngang là y = 3.
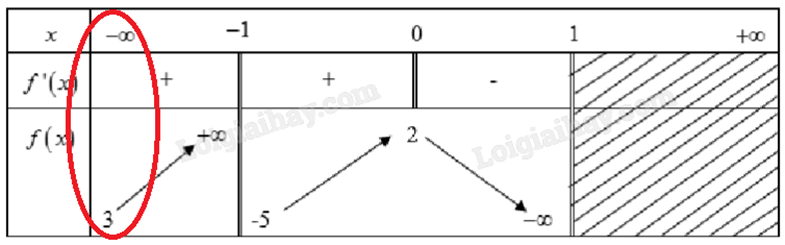
3. Cách tìm đường tiệm cận đứng dựa vào bảng biến thiên
Cho bảng biến thiên của hàm số y = f(x).
Đường thẳng \(x = {x_0}\) được gọi là tiệm cận đứng của đồ thị hàm số y = f(x) nếu thoả mãn ít nhất một trong các điều kiện:
+ \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty \);
+ \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty \);
+ \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty \);
+ \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \).
Ví dụ minh hoạ:
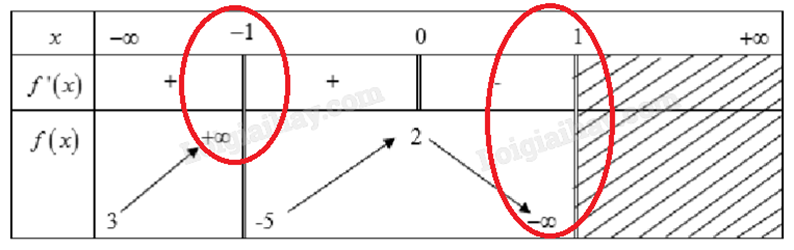
1) Cho bảng biến thiên của hàm số y = f(x):
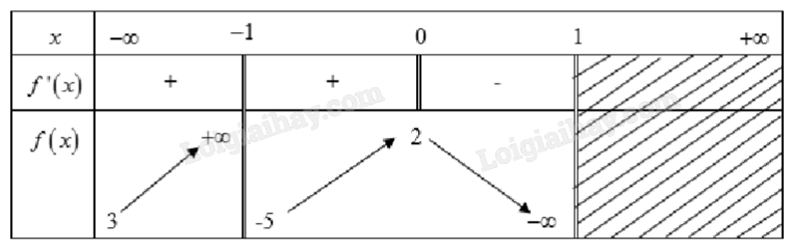
Vì \(\mathop {\lim }\limits_{x \to - {1^ - }} f(x) = + \infty \) và \(\mathop {\lim }\limits_{x \to {1^ - }} f(x) = - \infty \) nên đồ thị hàm số y = f(x) có hai tiệm cận đứng là x = -1 và x = 1.
2) Cho bảng biến thiên của hàm số y = f(x):
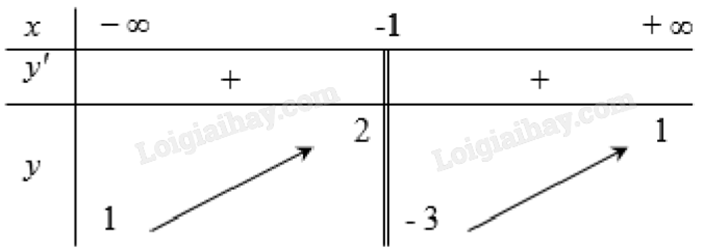
Vì không có giá trị \({x_0}\) nào thoả mãn 1 trong 4 điều kiện về giới hạn hàm số nên đồ thị không có tiệm cận đứng.

 Đường tiệm cận của đồ thị hàm số - Từ điển môn Toán 12
Đường tiệm cận của đồ thị hàm số - Từ điển môn Toán 12 






Danh sách bình luận