Cách tìm số điểm cực trị của hàm số chứa dấu giá trị tuyệt đối - Toán 12

Cho hàm số y = f(x) xác định trên tập hợp D và \({x_0} \in D\).

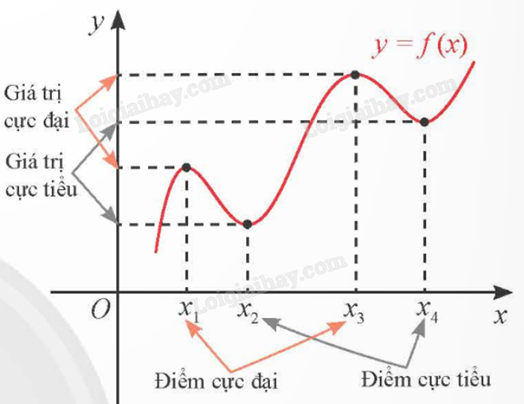
+ Nếu tồn tại khoảng \((a;b) \subset D\) chứa \({x_0}\) sao cho \(f(x) < f({x_0})\) với mọi \(x \in (a;b)\backslash \{ {x_0}\} \) thì \({x_0}\) được gọi là một điểm cực đại, \(f({x_0})\) được gọi là giá trị cực đại của hàm số y = f(x), kí hiệu là \({y_{CD}}\).

+ Nếu tồn tại khoảng \((a;b) \subset D\) chứa \({x_0}\) sao cho \(f(x) > f({x_0})\) với mọi \(x \in (a;b)\backslash \{ {x_0}\} \) thì \({x_0}\) được gọi là một điểm cực tiểu, \(f({x_0})\) được gọi là giá trị cực tiểu của hàm số y = f(x), kí hiệu là \({y_{CT}}\).

Cực đại, cực tiểu gọi chung là cực trị.

Đề bài yêu cầu tìm điểm cực trị của hàm số thì kết luận giá trị của x, giá trị cực trị của hàm số thì kết luận giá trị của y, điểm cực trị của đồ thị hàm số thì kết luận giá trị (x;y).

Bước 1: Từ đồ thị y = f(x), vẽ đồ thị y = |f(x)|.

- Giữ nguyên phần đồ thị phía trên trục Ox.

- Lấy đối xứng phần đồ thị phía dưới trục Ox qua Ox.

- Xoá phần đồ thị phía dưới Ox.

Bước 2: Quan sát đồ thị y = |f(x)| và kết luận số điểm cực trị.

Ví dụ minh hoạ:

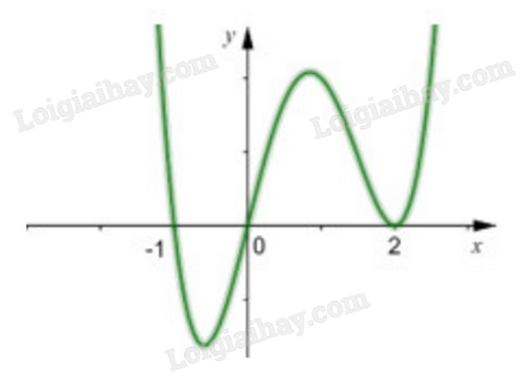
Cho hàm số y = f(x) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ. Số diểm cực trị của hàm số y = |f(x)| là bao nhiêu?

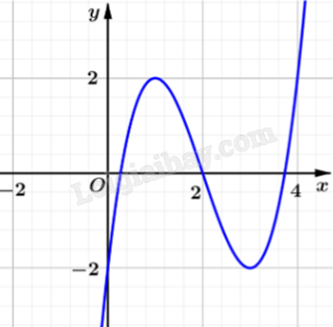
Giải:

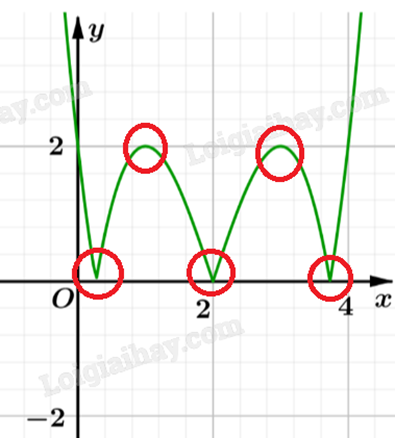
Ta có đồ thị hàm số y = |f(x)| như sau:

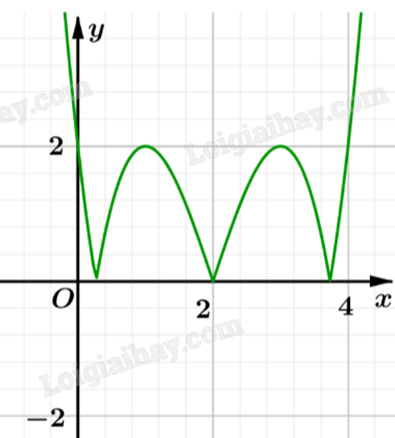
Vậy hàm số y = |f(x)| có 5 điểm cực trị.

Bước 1: Từ đồ thị y = f(x), vẽ đồ thị y = f(|x|).

- Giữ nguyên phần đồ thị bên phải trục Oy.

- Xoá phần đồ thị bên trái trục Oy.

- Lấy đối xứng phần đồ thị bên phải trục Oy qua Oy.

Bước 2: Quan sát đồ thị y = f(|x|) và kết luận số điểm cực trị.

Ví dụ minh hoạ:

Cho hàm số y = f(x) với đồ thị (C) như hình vẽ dưới. Hãy xác định hàm trị tuyệt đối y = f(|x|) gồm có bao nhiêu điểm cực trị?

Giải:

Ta có đồ thị hàm số y = f(|x|) như sau:

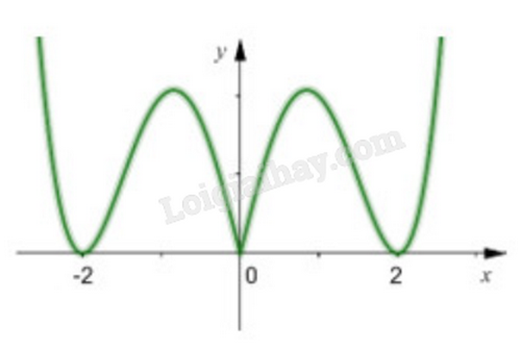
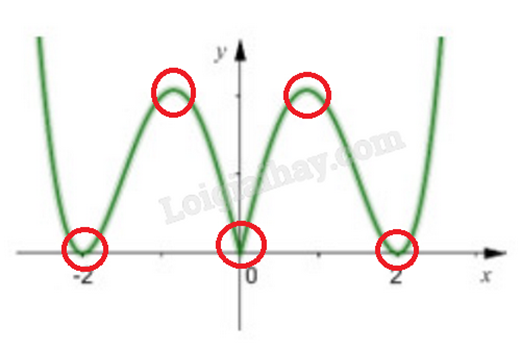
Vậy hàm số y = |f(x)| có 5 điểm cực trị.