Giá trị lớn nhất và giá trị nhỏ nhất của hàm số - Từ đi.. 
1. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số là gì?
Cho hàm số \(y = f(x)\) xác định trên tập \(D\).
- Số \(M\) là giá trị lớn nhất (GTLN) của hàm số \(f\) trên \(D \).
\(⇔\left\{ \matrix{
f(x) \le M,\forall x \in D \hfill \cr
\exists \, {x_0} \in D\text{ sao cho }f({x_0}) = M \hfill \cr} \right.\)
Kí hiệu: \(M=\underset{D}{\max} f(x)\).
- Số \(m\) là giá trị nhỏ nhất (GTNN) của hàm số \(f\) trên \(D\).
\(⇔\left\{ \matrix{
f(x) \ge m,\forall x \in D \hfill \cr
\exists \, {x_0} \in D\text{ sao cho }f({x_0}) = m \hfill \cr} \right.\)
Kí hiệu: \(m=\underset{D}{\min} f(x)\).
2. Cách tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số dựa vào bảng biến thiên
Cho bảng biến thiên của hàm số y = f(x) liên tục trên K.
- Giá trị lớn nhất của hàm số trên K là giá trị y lớn nhất trong bảng biến thiên trên K.
- Giá trị nhỏ nhất của hàm số trên K là giá trị y nhỏ nhất trong bảng biến thiên trên K.
Ví dụ minh hoạ:
Cho hàm số y = f(x) liên tục trên đoạn [–6;5] và có bảng biến thiên trong đoạn [–6;5] như hình.
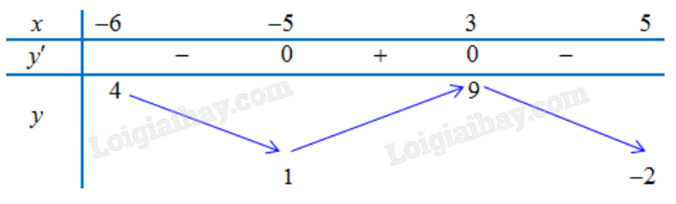
Giá trị y lớn nhất trên [-6;5] là 9 (ứng với x = 3), giá trị y nhỏ nhất trên [-6;5] là -2 (ứng với x = 5).
Vậy \(\mathop {\max }\limits_{[ - 6;5]} f(x) = f(3) = 9\) và \(\mathop {\min }\limits_{[ - 6;5]} f(x) = f(5) = - 2\).
