1. Cực tiểu, cực đại của hàm số là gì?
Cho hàm số y = f(x) xác định trên tập hợp D và \({x_0} \in D\).
+ Nếu tồn tại khoảng \((a;b) \subset D\) chứa \({x_0}\) sao cho \(f(x) < f({x_0})\) với mọi \(x \in (a;b)\backslash \{ {x_0}\} \) thì \({x_0}\) được gọi là một điểm cực đại, \(f({x_0})\) được gọi là giá trị cực đại của hàm số y = f(x), kí hiệu là \({y_{CD}}\).
+ Nếu tồn tại khoảng \((a;b) \subset D\) chứa \({x_0}\) sao cho \(f(x) > f({x_0})\) với mọi \(x \in (a;b)\backslash \{ {x_0}\} \) thì \({x_0}\) được gọi là một điểm cực tiểu, \(f({x_0})\) được gọi là giá trị cực tiểu của hàm số y = f(x), kí hiệu là \({y_{CT}}\).
Cực đại, cực tiểu gọi chung là cực trị.
Đề bài yêu cầu tìm điểm cực trị của hàm số thì kết luận giá trị của x, giá trị cực trị của hàm số thì kết luận giá trị của y, điểm cực trị của đồ thị hàm số thì kết luận giá trị (x;y).
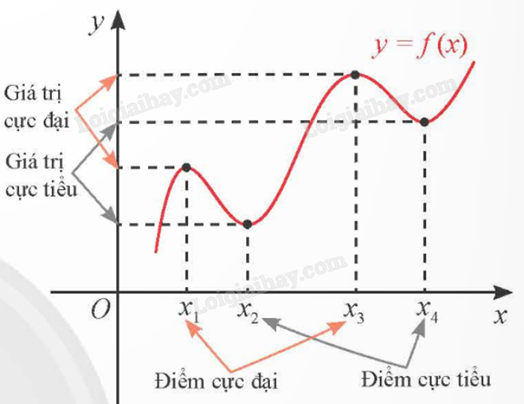
2. Cách tìm cực trị dựa vào đồ thị hàm số
Cho đồ thị hàm số y = f(x).
Tại điểm mà đồ thị đổi hướng:
- Lên \( \to \) xuống (trái sang phải): cực đại.
- Xuống \( \to \) lên (trái sang phải): cực tiểu.
Ví dụ minh hoạ:
a)
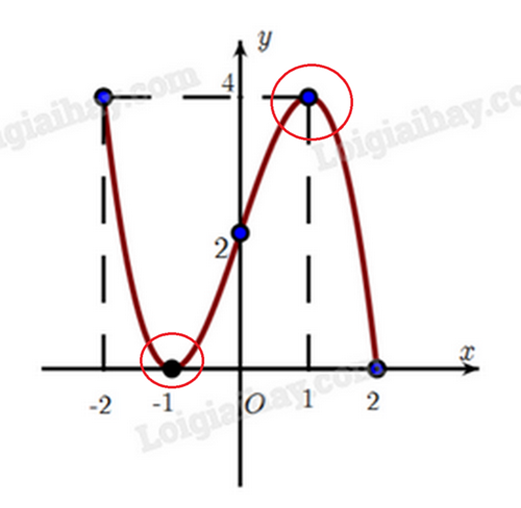
Điểm cực tiểu của hàm số: x = -1. Điểm cực đại của hàm số: x = 1.
Giá trị cực tiểu của hàm số: y = 0. Giá trị cực đại của hàm số là y = 4.
Điểm cực tiểu của đồ thị hàm số là (-1;0). Điểm cực đại của đồ thị hàm số là (1;4).
Hàm số y = f(x) có hai điểm cực trị, trong đó có một điểm cực đại và một điểm cực tiểu.
b)
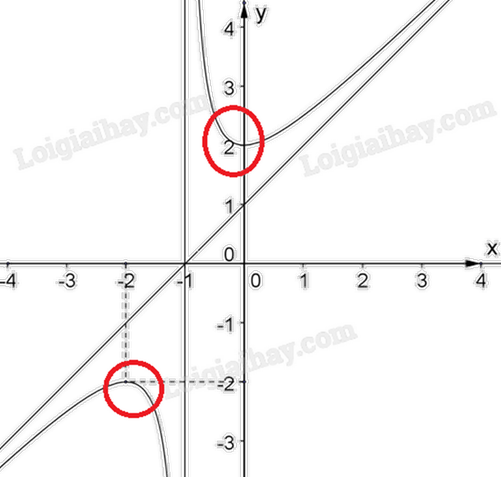
Điểm cực tiểu của hàm số: x = 0. Điểm cực đại của hàm số: x = -2.
Giá trị cực tiểu của hàm số: y = 2. Giá trị cực đại của hàm số là y = -2.
Điểm cực tiểu của đồ thị hàm số là (0;2). Điểm cực đại của đồ thị hàm số là (-2;-2).
Hàm số y = f(x) có hai điểm cực trị, trong đó có một điểm cực đại và một điểm cực tiểu.
3. Cách tìm cực trị dựa vào bảng biến thiên
Cho đồ thị hàm số y = f(x) liên tục trên K.
Cách 1: Quan sát hướng đồ thị. Qua điểm x thuộc K mà đồ thị đổi hướng:
- Lên \( \to \) xuống (trái sang phải): cực đại.
- Xuống \( \to \) lên (trái sang phải): cực tiểu.
Cách 2: Quan sát dấu của f’(x). Qua điểm x thuộc K mà f’(x) đổi dấu:
- Dương (+) \( \to \) âm (-): cực đại.
- Âm (-) \( \to \) dương (+): cực tiểu.
Ví dụ minh hoạ:
Cho hàm số y = f(x) có bảng biến thiên như sau:
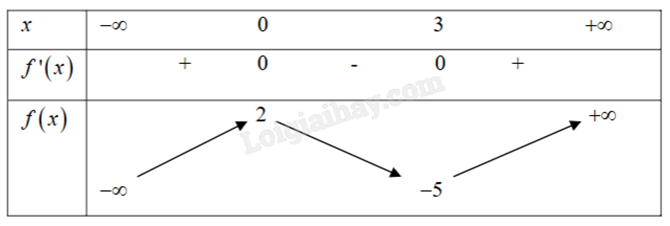
Cách 1:
- Qua x = 0, thấy hướng đồ thị từ trái sang theo hướng lên \( \to \) xuống nên hàm số y = f(x) có điểm cực đại là x = 0, giá trị cực đại là y = 2.
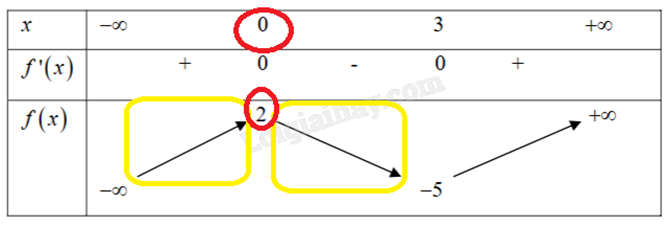
- Qua x = 3, thấy hướng đồ thị từ trái sang theo hướng xuống \( \to \) lên nên hàm số y = f(x) có điểm cực tiểu là x = 3, giá trị cực đại là y = -5.
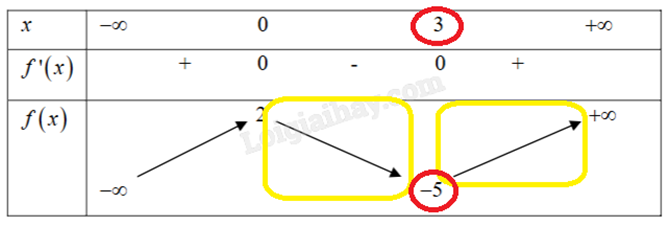
Cách 2:
- Qua x = 0, thấy dấu của f’(x) từ dương sang âm nên hàm số y = f(x) có điểm cực đại là x = 0, giá trị cực đại là y = 2.
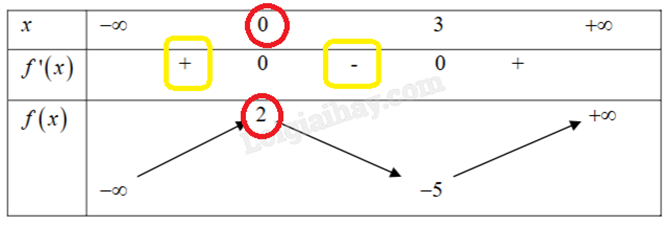
- Qua x = 3, thấy dấu của f’(x) từ âm sang dương nên hàm số y = f(x) có điểm cực tiểu là x = 3, giá trị cực đại là y = -5.
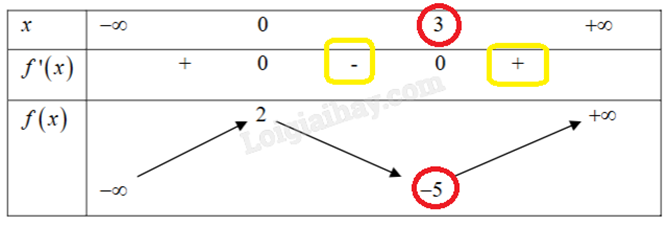
Hàm số y = f(x) có hai điểm cực trị, trong đó có một điểm cực đại và một điểm cực tiểu.
4. Cách tìm cực trị dựa vào công thức hàm số
Bước 1: Lập bảng biến thiên của hàm số y = f(x):
- Tìm tập xác định.
- Tính đạo hàm f’(x) và tìm nghiệm của phương trình f’(x) = 0 hoặc tại đó f’(x) không xác định.
- Tính các giới hạn (nếu có).
Bước 2: Quan sát bảng biến thiên và kết luận:
Cách 1: Quan sát hướng đồ thị. Qua điểm x thuộc tập xác định mà đồ thị đổi hướng:
- Lên \( \to \) xuống (trái sang phải): cực đại.
- Xuống \( \to \) lên (trái sang phải): cực tiểu.
Cách 2: Quan sát dấu của f’(x). Qua điểm x thuộc tập xác định mà f’(x) đổi dấu:
- Dương (+) \( \to \) âm (-): cực đại.
- Âm (-) \( \to \) dương (+): cực tiểu.
Ví dụ minh hoạ:
Tìm điểm cực trị của mỗi hàm số sau:
a) \(y = {x^3} - 12{\rm{x}} + 8\).
b) \(y = 2{{\rm{x}}^4} - 4{{\rm{x}}^2} - 1\).
c) \(y = \frac{{{x^2} - 2{\rm{x}} - 2}}{{x + 1}}\).
d) \(y = - x + 1 - \frac{9}{{x - 2}}\).
Giải:
a) Hàm số có tập xác định là \(\mathbb{R}\).
Ta có: \(y' = 3{{\rm{x}}^2} - 12\); \(y' = 0\) khi \(x = - 2,x = 2\).
Bảng biến thiên của hàm số:
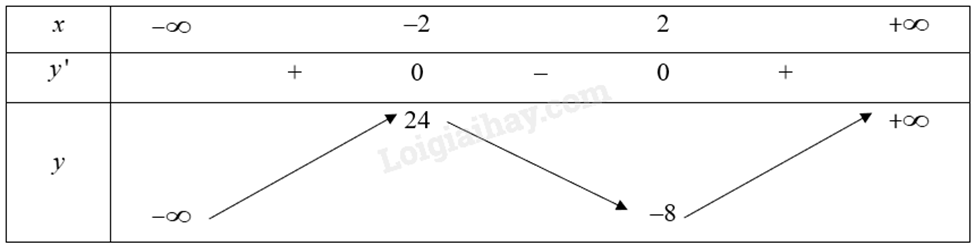
Vậy hàm số đạt cực tiểu tại \(x = 2\) và đạt cực đại tại \(x = - 2\).
b) Hàm số có tập xác định là \(\mathbb{R}\).
Ta có: \(y' = 8{{\rm{x}}^3} - 8{\rm{x}}\).
\(y' = 0\) khi \(x = 0,x = - 1,x = 1\).
Bảng biến thiên của hàm số:
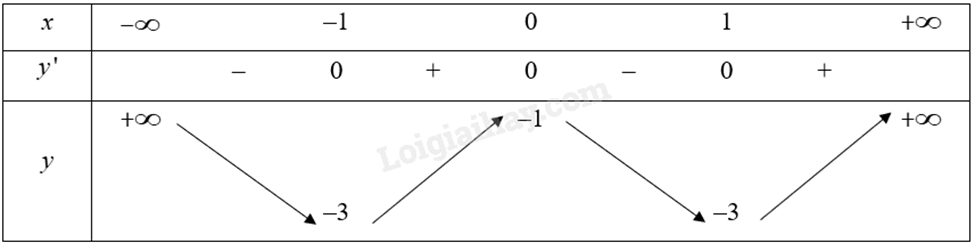
Vậy hàm số đạt cực tiểu tại \(x = - 1\) và \(x = 1\), đạt cực đại tại \(x = 0\).
c) Hàm số có tập xác định là \(\mathbb{R}\backslash \left\{ { - 1} \right\}\).
Ta có:
\(y' = \frac{{\left( {{x^2} - 2x - 2} \right)'.\left( {x + 1} \right) - \left( {{x^2} - 2x - 2} \right).\left( {x + 1} \right)'}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{\left( {2{\rm{x}} - 2} \right)\left( {x + 1} \right) - \left( {{x^2} - 2x - 2} \right)}}{{{{\left( {x + 1} \right)}^2}}}\)
\( = \frac{{{x^2} + 2{\rm{x}}}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{x\left( {{\rm{x}} + 2} \right)}}{{{{\left( {x + 1} \right)}^2}}}\).
\(y' = 0\) khi \(x = 0,x = - 2\).
Bảng biến thiên của hàm số:
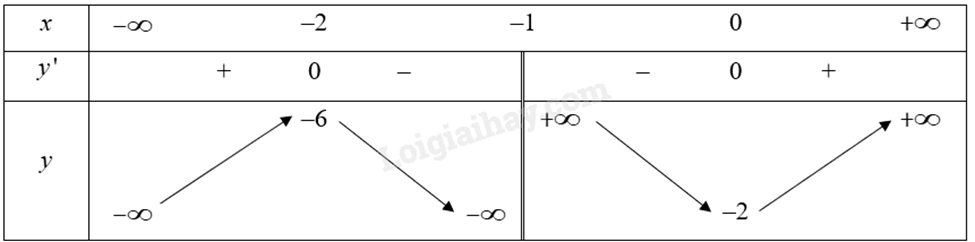
Vậy hàm số đạt cực tiểu tại \(x = 0\) và đạt cực đại tại \(x = - 2\).
d) Hàm số có tập xác định là \(\mathbb{R}\backslash \left\{ 2 \right\}\).
Ta có:
\(y' = - 1 + \frac{9}{{{{\left( {x - 2} \right)}^2}}} = \frac{{ - {x^2} + 4{\rm{x}} - 4 + 9}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{ - {x^2} + 4{\rm{x}} + 5}}{{{{\left( {x - 2} \right)}^2}}}\).
\(y' = 0\) khi \(x = 5,x = - 1\).
Bảng biến thiên của hàm số:
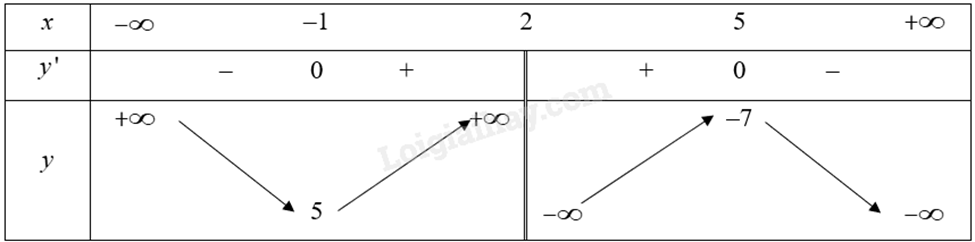
Vậy hàm số đạt cực tiểu tại \(x = - 1\) và đạt cực đại tại \(x = 5\).
5. Cách tìm cực trị dựa vào công thức hàm số f'(x)
Cho hàm số y = f(x) liên tục trên K.
Bước 1: Lập bảng xét dấu của f’(x).
Bước 2: Quan sát dấu của f’(x). Qua điểm x thuộc K mà f’(x) đổi dấu:
- Dương (+) \( \to \) âm (-): x là điểm cực đại.
- Âm (-) \( \to \) dương (+): x là điểm cực tiểu.
Ví dụ minh hoạ:
Xét sự biến thiên của của hàm số y = f(x) liên tục trên \(\mathbb{R}\) và có \(f'(x) = {(x + 1)^2}{(x - 1)^3}(2 - x)\).
Giải:
\(f'(x) = {(x + 1)^2}{(x - 1)^3}(2 - x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = 2\end{array} \right.\).
Lập bảng xét dấu như sau:
- Điền các nghiệm của phương trình f’(x) = 0 vừa tìm theo thứ tự từ nhỏ đến lớn (hàng 1).
- Tương ứng với các nghiệm x đó, giá trị của f’(x) = 0 (hàng 2).

- Cần điền dấu vào các khoảng trống để được bảng xét dấu hoàn thiện.
Xét khoảng \(( - \infty ; - 1)\): Lấy giá trị x bất kì trong khoảng \(( - \infty ; - 1)\) thay vào f’(x), giả sử x = -2:
\(f'( - 2) = {( - 2 + 1)^2}{( - 2 - 1)^3}(2 + 2) = - 108 < 0\). Vậy ta điền dấu “-”.

Làm tương tự với các khoảng còn lại, ta được bảng xét dấu hoàn thiện:

Quan sát bảng xét dấu, thấy:
+ f’(x) đổi dấu từ âm sang dương khi qua x = 1. Vậy x = 1 là điểm cực tiểu của hàm số.
+ f’(x) đổi dấu từ dương sang âm khi qua x = 2. Vậy x = 2 là điểm cực đại của hàm số.
6. Cách tìm cực trị dựa vào đồ thị hàm số f'(x)
Bước 1: Dựa vào đồ thị y = f’(x), lập bảng xét dấu của hàm số y = f(x).
- Lấy các mốc xét dấu là giao điểm của đồ thị y = f’(x) với trục hoành.
- Trên khoảng f’(x) > 0 (đồ thị f’(x) nằm phía trên trục hoành) thì điền dấu “+”.
- Trên khoảng f’(x) < 0 (đồ thị f’(x) nằm phía dưới trục hoành) thì điền dấu “+”.
Bước 2: Qua điểm x thuộc K mà f’(x) đổi dấu:
- Dương (+) \( \to \) âm (-): x là điểm cực đại.
- Âm (-) \( \to \) dương (+): x là điểm cực tiểu.
Ví dụ minh hoạ:
Cho hàm số y = f’(x) có đồ thị như hình:
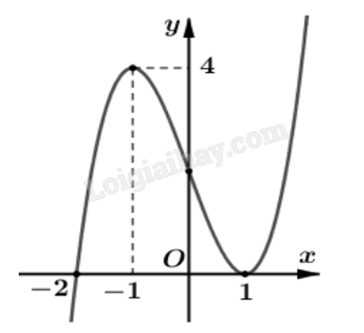
Đồ thị giao trục hoành tại hai điểm là x = -2 và x = 1.
Thấy trên khoảng \(( - \infty ; - 2)\), đồ thị y = f’(x) nằm phía dưới trục hoành; trên khoảng \(( - 2;1)\) và \((1; + \infty )\), đồ thị y = f’(x) nằm phía trên trục hoành.
Ta lập bảng xét dấu:

Quan sát bảng xét dấu, thấy f’(x) đổi dấu từ âm sang dương khi qua x = -2. Vậy x = -2 là điểm cực tiểu của hàm số.

 Tính đơn điệu và cực trị của hàm số - Từ điển môn Toán 12
Tính đơn điệu và cực trị của hàm số - Từ điển môn Toán 12 






Danh sách bình luận