Giới hạn vô cực của hàm số tại một điểm - Toán 11

- Cho hàm số \(y = f(x)\) xác định trên khoảng \((a; + \infty )\).

Ta nói hàm số \(y = f(x)\) có giới hạn là \( + \infty \) khi \(x \to {a^ + }\) nếu với dãy số \(({x_n})\) bất kì, \({x_n} > a\) và \({x_n} \to a\), ta có \(f({x_n}) \to  + \infty \).

Kí hiệu \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) =  + \infty \) hay \(f(x) \to  + \infty \) khi \(x \to {a^ + }\).

- Các trường hợp \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) =  - \infty \); \(\mathop {\lim }\limits_{x \to {a^ - }} f(x) =  + \infty \); \(\mathop {\lim }\limits_{x \to {a^ - }} f(x) =  - \infty \) được định nghĩa tương tự.

Ta có các giới hạn thường dùng sau:

\(\mathop {\lim }\limits_{x \to {a^ + }} \frac{1}{{x - a}} =  + \infty \) và \(\mathop {\lim }\limits_{x \to {a^ - }} \frac{1}{{x - a}} =  - \infty \) \((a \in \mathbb{R})\).

Quy tắc tìm giới hạn của tích \(f(x).g(x)\):

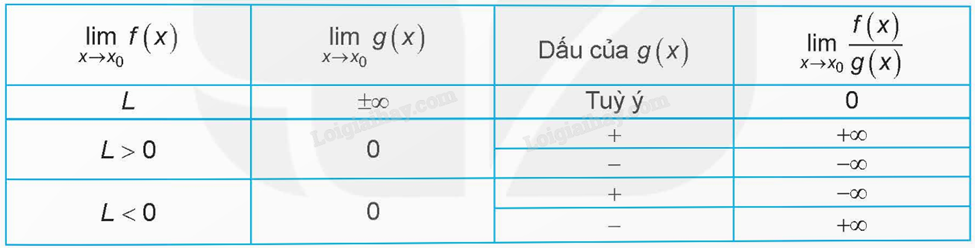
Quy tắc tìm giới hạn của thương \(\frac{{f(x)}}{{g(x)}}\):

1) Tính \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{1}{{x - 2}}\).

Giải:

Ta có: \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{1}{{x - 2}} =  + \infty \).

2) Tính \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{1 - 2x}}{{x - 2}}\).

Giải:

a) Ta có \(\mathop {\lim }\limits_{x \to {2^ + }} (1 - 2x) = 1 - 2\mathop {\lim }\limits_{x \to {2^ + }} x = 1 - 2 \cdot 2 =  - 3;\mathop {\lim }\limits_{x \to {2^ + }} \frac{1}{{x - 2}} =  + \infty .\)

Do đó \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{1 - 2x}}{{x - 2}} = \mathop {\lim }\limits_{x \to {2^ + }} \left[ {(1 - 2x) \cdot \frac{1}{{x - 2}}} \right] =  - \infty .\)

3) Tính \(\mathop {\lim }\limits_{x \to 0} \frac{{x + 1}}{{{x^2}}}\).

Giải:

Ta sử dụng quy tắc tìm giới hạn của thương. Rõ ràng, giới hạn của tử số \(\mathop {\lim }\limits_{x \to 0} (x + 1) = 1\).

Ngoài ra, mẫu số nhận giá trị dương với mọi \(x \ne 0\) và \(\mathop {\lim }\limits_{x \to 0} {x^2} = 0\).

Do vậy \(\mathop {\lim }\limits_{x \to 0} \frac{{x + 1}}{{{x^2}}} =  + \infty \).

4) Tính \(\mathop {\lim }\limits_{x \to {1^ + }} \frac{1}{{x(1 - x)}}\) và \(\mathop {\lim }\limits_{x \to {1^ - }} \frac{1}{{x(1 - x)}}\).

Giải:

Viết \(\frac{1}{{x(1 - x)}} = \frac{1}{x} \cdot \frac{1}{{1 - x}}\), ta có \(\mathop {\lim }\limits_{x \to {1^ + }} \frac{1}{x} = 1 > 0\).

Hơn nữa \(\mathop {\lim }\limits_{x \to {1^ + }} \frac{1}{{1 - x}} =  - \infty \) do \(1 - x < 0\) khi \(x > 1\).

Áp dụng quy tắc tìm giới hạn của tích, ta được \(\mathop {\lim }\limits_{x \to {1^ + }} \frac{1}{{x(1 - x)}} =  - \infty \).

Lí luận tương tự, ta có \(\mathop {\lim }\limits_{x \to {1^ - }} \frac{1}{{x(1 - x)}} =  + \infty \).