Cách tính giới hạn hàm số theo dạng - Toán 11

a) Phương pháp giải:

Khử dạng vô định bằng cách phân tích đa thức thành nhân tử bằng sơ đồ Hoocne, sau đó đơn giản biểu thức để khử dạng vô định.

Lưu ý:

+ \(f(x) = a{x^2} + bx + c = a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\) với \({x_1}\), \({x_2}\) là nghiệm của phương trình f(x) = 0. Học sinh thường quên nhân thêm a.

+ Hằng đẳng thức: \({x^n} - 1 = (x - 1)({x^{n - 1}} + {x^{n - 2}} + ... + {x^2} + x + 1)\).

b) Ví dụ minh hoạ:

1) Tính giới hạn \(A = \mathop {\lim }\limits_{x \to 2} \frac{{2{x^2} + 3x - 14}}{{{x^2} - 4}}\).

Giải:

\(A = \mathop {\lim }\limits_{x \to 2} \frac{{2{x^2} + 3x - 14}}{{{x^2} - 4}} = \mathop {\lim }\limits_{x \to 2} \frac{{2(x - 2)\left( {x + \frac{7}{2}} \right)}}{{(x - 2)(x + 2)}} = \mathop {\lim }\limits_{x \to 2} \frac{{2x + 7}}{{x + 2}} = \frac{{11}}{4}\).

2) Tính giới hạn \(A = \mathop {\lim }\limits_{x \to 2} \frac{{2{x^3} - 5{x^2} - 2x - 3}}{{4{x^3} - 13{x^2} + 4x - 3}}\).

Giải:

Sử dụng sơ đồ Hoocne (đầu rơi, nhân tới, cộng chéo):

Phân tích \(2{x^3} - 5{x^2} - 2x - 3\) thành nhân tử:

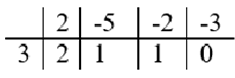
Suy ra \(2{x^3} - 5{x^2} - 2x - 3 = (x - 3)(2{x^2} + x + 1)\).

Phân tích \(4{x^3} - 13{x^2} + 4x - 3\) thành nhân tử:

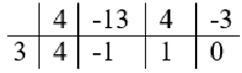
Suy ra \(4{x^3} - 13{x^2} + 4x - 3 = (x - 3)(4{x^2} - x + 1)\).

\(A = \mathop {\lim }\limits_{x \to 3} \frac{{2{x^3} - 5{x^2} - 2x - 3}}{{4{x^3} - 13{x^2} + 4x - 3}} = \mathop {\lim }\limits_{x \to 3} \frac{{(x - 3)(2{x^2} + x + 1)}}{{(x - 3)(4{x^2} - x + 1)}} = \mathop {\lim }\limits_{x \to 3} \frac{{2{x^2} + x + 1}}{{4{x^2} - x + 1}} = \frac{{11}}{{17}}\).

3) Tính giới hạn \(A = \mathop {\lim }\limits_{x \to 1} \frac{{{x^{100}} - 2x + 1}}{{{x^{50}} - 2x + 1}}\).

Giải:

Ta có \(A = \mathop {\lim }\limits_{x \to 1} \frac{{{x^{100}} - 2x + 1}}{{{x^{50}} - 2x + 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{({x^{100}} - x) - (x - 1)}}{{({x^{50}} - x) - (x - 1)}} = \mathop {\lim }\limits_{x \to 1} \frac{{x({x^{99}} - 1) - (x - 1)}}{{x({x^{49}} - 1) - (x - 1)}}\)

\( = \mathop {\lim }\limits_{x \to 1} \frac{{x(x - 1)({x^{98}} + {x^{97}} + {x^{96}} +  \ldots  + x + 1) - (x - 1)}}{{x(x - 1)({x^{48}} + {x^{47}} + {x^{46}} +  \ldots  + x + 1) - (x - 1)}}\)

\( = \mathop {\lim }\limits_{x \to 1} \frac{{(x - 1)({x^{99}} + {x^{98}} + {x^{97}} +  \ldots  + {x^2} + x - 1)}}{{(x - 1)({x^{49}} + {x^{48}} + {x^{47}} +  \ldots  + {x^2} + x - 1)}}\)

\( = \mathop {\lim }\limits_{x \to 1} \frac{{({x^{99}} + {x^{98}} + {x^{97}} +  \ldots  + {x^2} + x - 1)}}{{({x^{49}} + {x^{48}} + {x^{47}} +  \ldots  + {x^2} + x - 1)}} = \frac{{98}}{{48}} = \frac{{49}}{{24}}\).

a) Phương pháp giải:

Nhân liên hợp để khử dạng vô định.

Liên hợp là hình thức trục căn dựa vào hằng đẳng thức: \(\left\{ \begin{array}{l}(a - b)(a + b) = {a^2} - {b^2}\\(a \pm b)({a^2} \mp ab + {b^2}) = {a^3} \pm {b^3}\end{array} \right.\)

Một số công thức cần nhớ:

\(\sqrt a  - \sqrt b  = \frac{{a - b}}{{\sqrt a  + \sqrt b }}\);

\(\sqrt a  - b = \frac{{a - {b^2}}}{{\sqrt a  + b}}\);

\(\sqrt[3]{a} + \sqrt[3]{b} = \frac{{a + b}}{{\sqrt[3]{{{a^2}}} - \sqrt[3]{{ab}} + \sqrt[3]{{{b^2}}}}}\);

\(\sqrt[3]{a} - \sqrt[3]{b} = \frac{{a - b}}{{\sqrt[3]{{{a^2}}} + \sqrt[3]{{ab}} + \sqrt[3]{{{b^2}}}}}\);

\(\sqrt[3]{a} + b = \frac{{a + {b^3}}}{{\sqrt[3]{{{a^2}}} - \sqrt[3]{a}b + {b^2}}}\);

\(\sqrt[3]{a} - b = \frac{{a - {b^3}}}{{\sqrt[3]{{{a^2}}} + \sqrt[3]{a}b + {b^2}}}\).

b) Ví dụ minh hoạ:

1) Tính giới hạn \(B = \mathop {\lim }\limits_{x \to 6} \frac{{3 - \sqrt {x + 3} }}{{x - 6}}\).

Giải:

\(B = \mathop {\lim }\limits_{x \to 6} \frac{{3 - \sqrt {x + 3} }}{{x - 6}} = \mathop {\lim }\limits_{x \to 6} \frac{{\left( {3 - \sqrt {x + 3} } \right)\left( {3 + \sqrt {x + 3} } \right)}}{{\left( {x - 6} \right)\left( {3 + \sqrt {x + 3} } \right)}}\)

\( = \mathop {\lim }\limits_{x \to 6} \frac{{9 - (x + 3)}}{{(x - 6)\left( {3 + \sqrt {x + 3} } \right)}} = \mathop {\lim }\limits_{x \to 6} \frac{{6 - x}}{{(x - 6)\left( {3 + \sqrt {x + 3} } \right)}} = \mathop {\lim }\limits_{x \to 6} \frac{{ - 1}}{{3 + \sqrt {x + 3} }} = \frac{{ - 1}}{{3 + \sqrt {6 + 3} }} =  - \frac{1}{6}\).

2) Tính giới hạn \(E = \mathop {\lim }\limits_{x \to 2} \frac{{\sqrt[3]{{3x + 2}} - \sqrt {5x - 6} }}{{x - 2}}\).

Giải:

Giải phương trình \(\sqrt[3]{{3x + 2}} - \sqrt {5x - 6}  = 0\) (bấm máy tính) được nghiệm x = 2, ta thêm bớt 2:

Ta có \(E = \mathop {\lim }\limits_{x \to 2} \frac{{\sqrt[3]{{3x + 2}} - 2 + 2 - \sqrt {5x - 6} }}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{\sqrt[3]{{3x + 2}} - 2}}{{x - 2}} + \mathop {\lim }\limits_{x \to 2} \frac{{2 - \sqrt {5x - 6} }}{{x - 2}}\).

\(A = \mathop {\lim }\limits_{x \to 2} \frac{{\sqrt[3]{{3x + 2}} - 2}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{3x + 2 - 8}}{{(x - 2)(\sqrt[3]{{{{(3x + 2)}^2}}} + 2\sqrt[3]{{3x + 2}} + 4)}}\)

\( = \mathop {\lim }\limits_{x \to 2} \frac{{3(x - 2)}}{{(x - 2)(\sqrt[3]{{{{(3x + 2)}^2}}} + 2\sqrt[3]{{3x + 2}} + 4)}} = \mathop {\lim }\limits_{x \to 2} \frac{3}{{\sqrt[3]{{{{(3x + 2)}^2}}} + 2\sqrt[3]{{3x + 2}} + 4}} = \frac{1}{4}\).

\(B = \mathop {\lim }\limits_{x \to 2} \frac{{2 - \sqrt {5x - 6} }}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{4 - (5x - 6)}}{{(x - 2)(2 + \sqrt {5x - 6} )}} = \mathop {\lim }\limits_{x \to 2} \frac{{5(2 - x)}}{{(x - 2)(2 + \sqrt {5x - 6} )}}\)

\( = \mathop {\lim }\limits_{x \to 2} \frac{{ - 5}}{{2 + \sqrt {5x - 6} }} =  - \frac{5}{4}\).

Vậy \(E = A + B = \frac{1}{4} - \frac{5}{4} =  - 1\).

3) Tính giới hạn \(L = \mathop {\lim }\limits_{x \to  - 1} \frac{{\sqrt[3]{{5x - 3}} + 2}}{{x + 1}}\).

Giải:

\(L = \mathop {\lim }\limits_{x \to  - 1} \frac{{\sqrt[3]{{5x - 3}} + 2}}{{x + 1}} = \mathop {\lim }\limits_{x \to  - 1} \frac{{5x - 3 + 8}}{{(x + 1)(\sqrt[3]{{{{(5x - 3)}^2}}} - 2\sqrt[3]{{5x - 3}} + 4)}}\)

\( = \mathop {\lim }\limits_{x \to  - 1} \frac{{5x + 5}}{{(x + 1)(\sqrt[3]{{{{(5x - 3)}^2}}} - 2\sqrt[3]{{5x - 3}} + 4)}} = \mathop {\lim }\limits_{x \to  - 1} \frac{5}{{\sqrt[3]{{{{(5x - 3)}^2}}} - 2\sqrt[3]{{5x - 3}} + 4}} = \frac{5}{{12}}\).

4) Tính giới hạn \(\mathop {\lim }\limits_{x \to 2} \frac{{\sqrt[3]{{3x + 2}} - \sqrt {3x - 2} }}{{x - 2}}\).

Giải:

Giải phương trình \(\sqrt[3]{{3x + 2}} - \sqrt {3x - 2}  = 0\) (bấm máy tính) được nghiệm x = 2, ta thêm bớt 2:

Ta có \(E = \mathop {\lim }\limits_{x \to 2} \frac{{\sqrt[3]{{3x + 2}} - 2 - \sqrt {3x - 2}  + 2}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{\sqrt[3]{{3x + 2}} - 2}}{{x - 2}} - \mathop {\lim }\limits_{x \to 2} \frac{{\sqrt {3x - 2}  - 2}}{{x - 2}}\)

\( = \mathop {\lim }\limits_{x \to 2} \frac{{3x + 2 - 8}}{{(x - 2)(\sqrt[3]{{{{(3x + 2)}^2}}} + 2\sqrt[3]{{3x + 2}} + 4)}} - \mathop {\lim }\limits_{x \to 2} \frac{{3x - 2 - 4}}{{(x - 2)(\sqrt {3x - 2}  + 2)}}\)

\( = \mathop {\lim }\limits_{x \to 2} \frac{3}{{\sqrt[3]{{{{(3x + 2)}^2}}} + 2\sqrt[3]{{3x + 2}} + 4}} - \mathop {\lim }\limits_{x \to 2} \frac{3}{{\sqrt {3x - 2}  + 2}} = \frac{3}{{12}} - \frac{3}{4} =  - \frac{1}{2}\).

a) Phương pháp giải:

- Đối với dạng đa thức không cần, ta rút bậc cao và áp dụng công thức khi \(x \to  + \infty \).

+ \(\mathop {\lim }\limits_{x \to  + \infty } {x^k} =  + \infty \);

+ \(\mathop {\lim }\limits_{x \to  - \infty } {x^k} = \left\{ {\begin{array}{*{20}{l}}{ + \infty }&{khi}\\{ - \infty }&{khi}\end{array}} \right.\begin{array}{*{20}{c}}{}\\{}\end{array}\begin{array}{*{20}{c}}{k = 2l}\\{k = 2l + 1}\end{array}\);

+ \(\mathop {\lim }\limits_{x \to  + \infty } \frac{c}{{{x^k}}} = 0\) (c hằng số).

- Đối với dạng phân số không cần, ta làm tương tự như giới hạn dãy số, tức rút bậc cao nhất của tử và mẫu, sau đó áp dụng công thức trên.

- Ngoài việc đưa ra khỏi căn bậc chẵn cần có trị tuyệt đối, học sinh cần phân biệt khi nào đưa ra ngoài căn, khi nào liên hợp. Phương pháp suy luận cũng tương tự như giới hạn của dãy số, nhưng cần phân biệt khi \(x \to  + \infty \) hoặc \(x \to  - \infty \).

b) Ví dụ minh hoạ:

1) Tính giới hạn \(A = \mathop {\lim }\limits_{x \to  + \infty } \left( { - {x^3} - 6{x^2} + 9x + 1} \right)\).

\(A = \mathop {\lim }\limits_{x \to  + \infty } {x^3}\left( { - 1 - \frac{6}{x} + \frac{9}{{{x^2}}} + \frac{1}{{{x^3}}}} \right) =  - \infty \) (vì \(\mathop {\lim }\limits_{x \to  + \infty } {x^3} =  + \infty \) và \(\mathop {\lim }\limits_{x \to  + \infty } \left( { - 1 - \frac{6}{x} + \frac{9}{{{x^2}}} + \frac{1}{{{x^3}}}} \right) =  - 1\)).

2) Tính giới hạn \(B = \mathop {\lim }\limits_{x \to  + \infty } \frac{{{x^3} + 3x + 1}}{{2 - 6{x^2} - 6{x^3}}}\).

Giải:

\(B = \mathop {\lim }\limits_{x \to  + \infty } \frac{{{x^3}\left( {1 + \frac{3}{{{x^2}}} + \frac{1}{{{x^3}}}} \right)}}{{{x^3}\left( {\frac{2}{{{x^3}}} - \frac{6}{x} - 6} \right)}} = \mathop {\lim }\limits_{x \to  + \infty } \frac{{1 + \frac{3}{{{x^2}}} + \frac{1}{{{x^3}}}}}{{\frac{2}{{{x^3}}} - \frac{6}{x} - 6}} = \frac{{1 + 0 + 0}}{{0 - 0 - 6}} =  - \frac{1}{6}\).

3) Tính giới hạn \(C = \mathop {\lim }\limits_{x \to  - \infty } \sqrt {{x^2} + x + 1}  + 2x\).

Giải:

\(C = \mathop {\lim }\limits_{x \to  - \infty } \left[ {\sqrt {{x^2}\left( {1 + \frac{1}{x} + \frac{1}{{{x^2}}}} \right)}  + 2x} \right] = \mathop {\lim }\limits_{x \to  - \infty } \left( {\left| x \right|\sqrt {1 + \frac{1}{x} + \frac{1}{{{x^2}}}}  + 2x} \right)\)

\( = \mathop {\lim }\limits_{x \to  - \infty } \left( { - x\sqrt {1 + \frac{1}{x} + \frac{1}{{{x^2}}}}  + 2x} \right) = \mathop {\lim }\limits_{x \to  - \infty } x\left( {2 - \sqrt {1 + \frac{1}{x} + \frac{1}{{{x^2}}}} } \right) =  - \infty \).

(Vì \(\mathop {\lim }\limits_{x \to  - \infty } x =  - \infty \) và \(\mathop {\lim }\limits_{x \to  - \infty } \left[ {2 - \sqrt {1 + \frac{1}{x} + \frac{1}{{{x^2}}}} } \right] = 2 - 1 = 1 > 0)\).

a) Phương pháp giải:

Sử dụng các định lí về giới hạn hàm số.

\(x \to {x_0}^ +  \Rightarrow x > {x_0} \Leftrightarrow x - {x_0} > 0\);

\(x \to {x_0}^ -  \Rightarrow x < {x_0} \Leftrightarrow x - {x_0} < 0\).

b) Ví dụ minh hoạ:

1) Tính giới hạn \(A = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{2x - 3}}{{x - 1}}\).

Giải:

\(\left\{ {\begin{array}{*{20}{l}}{\mathop {\lim }\limits_{x \to {1^ + }} 2x - 3 =  - 1 < 0}\\\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} x - 1 = 0\\x \to {1^ + } \Rightarrow x > 1 \Rightarrow x - 1 > 0\end{array}\end{array}} \right. \Rightarrow A = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{2x - 3}}{{x - 1}} =  - \infty \).

2) Tính giới hạn \(A = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{x - 15}}{{x - 2}}\).

Giải:

\(\left\{ {\begin{array}{*{20}{l}}{\mathop {\lim }\limits_{x \to {2^ + }} x - 15 =  - 13 < 0}\\{\mathop {\lim }\limits_{x \to {2^ + }} x - 2 = 0}\\{x \to {2^ + } \Rightarrow x > 2 \Rightarrow x - 2 > 0}\end{array}} \right. \Rightarrow A = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{x - 15}}{{x - 2}} =  - \infty \)

3) Tính giới hạn \(A = \mathop {\lim }\limits_{x \to {3^ - }} \frac{{2 - x}}{{3 - x}}\).

Giải:

\(\left\{ {\begin{array}{*{20}{l}}{\mathop {\lim }\limits_{x \to {3^ - }} (2 - x) =  - 1 < 0}\\{\mathop {\lim }\limits_{x \to {3^ - }} (3 - x) = 0}\\{x \to {3^ - } \Rightarrow x < 3 \Rightarrow 3 - x > 0}\end{array}} \right. \Rightarrow A = \mathop {\lim }\limits_{x \to {3^ - }} \frac{{2 - x}}{{3 - x}} =  - \infty \).

4) Tính giới hạn \(A = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{x + 1}}{{2x - 4}}\).

Giải:

\(\left\{ {\begin{array}{*{20}{l}}{\mathop {\lim }\limits_{x \to {2^ + }} (x + 1) = 3 > 0}\\{\mathop {\lim }\limits_{x \to {2^ + }} (2x - 4) = 0}\\{x \to {2^ + } \Rightarrow x > 2 \Rightarrow 2x - 4 > 0}\end{array}} \right. \Rightarrow A = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{x + 1}}{{2x - 4}} =  + \infty \).

5) Tính giới hạn \(A = \mathop {\lim }\limits_{x \to {4^ - }} \frac{{x - 5}}{{{{(x - 4)}^2}}}\).

Giải:

\(\left\{ {\begin{array}{*{20}{l}}{\mathop {\lim }\limits_{x \to {4^ - }} (x - 5) =  - 1 < 0}\\{\mathop {\lim }\limits_{x \to {4^ - }} {{(x - 4)}^2} = 0}\\{x \to {4^ - } \Rightarrow {{(x - 4)}^2} > 0}\end{array}} \right. \Rightarrow A = \mathop {\lim }\limits_{x \to {4^ - }} \frac{{x - 5}}{{{{(x - 4)}^2}}} =  - \infty \).

6) Tính giới hạn \(A = \mathop {\lim }\limits_{x \to {3^ - }} \frac{{3x - 8}}{{{{(3 - x)}^2}}}\).

Giải:

\(\left\{ {\begin{array}{*{20}{l}}{\mathop {\lim }\limits_{x \to {3^ - }} (3x - 8) = 1 > 0}\\{\mathop {\lim }\limits_{x \to {3^ - }} {{(3 - x)}^2} = 0}\\{x \to {3^ - } \Rightarrow {{(3 - x)}^2} > 0}\end{array}} \right. \Rightarrow A = \mathop {\lim }\limits_{x \to {3^ - }} \frac{{3x - 8}}{{{{(3 - x)}^2}}} =  + \infty \).

7) Tính giới hạn \(\mathop {\lim }\limits_{x \to {{( - 3)}^ + }} \frac{{2{x^2} + 5x - 3}}{{{{(x + 3)}^2}}}\).

Giải:

Ta có \(\mathop {\lim }\limits_{x \to {{( - 3)}^ + }} \frac{{2{x^2} + 5x - 3}}{{{{(x + 3)}^2}}} = \mathop {\lim }\limits_{x \to {{( - 3)}^ + }} \frac{{(2x - 1)(x + 3)}}{{{{(x + 3)}^2}}} = \mathop {\lim }\limits_{x \to {{( - 3)}^ + }} \frac{{2x - 1}}{{x + 3}}\).

\(\left\{ {\begin{array}{*{20}{l}}{\mathop {\lim }\limits_{x \to {{( - 3)}^ + }} (2x - 1) =  - 7 < 0}\\{\mathop {\lim }\limits_{x \to {{( - 3)}^ + }} (x + 3) = 0}\\{x \to {{( - 3)}^ + } \Rightarrow x >  - 3 \Rightarrow x + 3 > 0}\end{array}} \right. \Rightarrow A = \mathop {\lim }\limits_{x \to {{( - 3)}^ + }} \frac{{2{x^2} + 5x - 3}}{{{{(x + 3)}^2}}} =  - \infty \).

8) Tính giới hạn \(A = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{1}{{x - 2}} - \frac{1}{{{x^2} - 4}}} \right)\).

Giải:

Ta có: \(A = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{1}{{x - 2}} - \frac{1}{{{x^2} - 4}}} \right) = \mathop {\lim }\limits_{x \to {2^ - }} \frac{{x + 1}}{{(x - 2)(x + 2)}}\).

\(\left\{ {\begin{array}{*{20}{l}}{\mathop {\lim }\limits_{x \to {2^ - }} (x + 1) = 3 > 0}\\{\mathop {\lim }\limits_{x \to {2^ - }} \left[ {(x - 2)(x + 2)} \right] = 0}\\{x \to {2^ - } \Rightarrow x < 2 \Rightarrow (x - 2)(x + 2) < 0}\end{array}} \right. \Rightarrow A = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{1}{{x - 2}} - \frac{1}{{{x^2} - 4}}} \right) =  - \infty \).

9) Tính giới hạn \(B = \mathop {\lim }\limits_{x \to {2^ - }} \frac{{|2 - x|}}{{2{x^2} - 5x + 2}}\).

Giải:

Vì \(x \to {2^ - } \Rightarrow x < 2 \Rightarrow |2 - x| = 2 - x\)

Do đó \(B = \mathop {\lim }\limits_{x \to {2^ - }} \frac{{2 - x}}{{(x - 2)(2x - 1)}} = \mathop {\lim }\limits_{x \to {2^ - }} \frac{{ - 1}}{{2x - 1}} =  - \frac{1}{3}\).

10) Tính giới hạn \(B = \mathop {\lim }\limits_{x \to {3^ + }} \frac{{|x - 3|}}{{5x - 15}}\).

Giải:

Vì \(x \to {3^ + } \Rightarrow x > 3 \Rightarrow |x - 3| = x - 3\).

Do đó \(B = \mathop {\lim }\limits_{x \to {3^ + }} \frac{{x - 3}}{{5(x - 3)}} = \mathop {\lim }\limits_{x \to {3^ + }} \frac{1}{5} = \frac{1}{5}\).

a) Phương pháp giải:

- Sử dụng các định lí về giới hạn hàm số.

- Sử dụng các công thức biến đổi lượng giác.

Lưu ý: \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1\).

b) Ví dụ minh hoạ:

1) Tính giới hạn \(A = \mathop {\lim }\limits_{x \to \frac{\pi }{6}} \frac{{2\sin x - 1}}{{4{{\cos }^2}x - 3}}\) | Đs: \(A =  - \frac{1}{2}\).

Giải:

\(A = \mathop {\lim }\limits_{x \to \frac{\pi }{6}} \frac{{2\sin x - 1}}{{4{{\cos }^2}x - 3}} = \mathop {\lim }\limits_{x \to \frac{\pi }{6}} \frac{{2\sin x - 1}}{{4(1 - {{\sin }^2}x) - 3}} = \mathop {\lim }\limits_{x \to \frac{\pi }{6}} \frac{{2\sin x - 1}}{{1 - 4{{\sin }^2}x}} = \mathop {\lim }\limits_{x \to \frac{\pi }{6}} \frac{{ - 1}}{{1 + 2\sin x}} =  - \frac{1}{2}\).

2) Tính giới hạn \(A = \mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{\sqrt 2 \sin x - 1}}{{2{{\cos }^2}x - 1}}\).

Giải:

\(A = \mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{\sqrt 2 \sin x - 1}}{{2{{\cos }^2}x - 1}} = \mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{\sqrt 2 \sin x - 1}}{{2(1 - {{\sin }^2}x) - 1}} = \mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{\sqrt 2 \sin x - 1}}{{1 - 2{{\sin }^2}x}} = \mathop {\lim }\limits_{x \to \frac{\pi }{4}} \frac{{ - 1}}{{1 + \sqrt 2 \sin x}} =  - \frac{1}{2}\).

3) Tính giới hạn \(A = \mathop {\lim }\limits_{x \to 0} \frac{{\cos 4x - 1}}{{\sin 4x}}\).

Giải:

\(A = \mathop {\lim }\limits_{x \to 0} \frac{{\cos 4x - 1}}{{\sin 4x}} = \mathop {\lim }\limits_{x \to 0} \frac{{ - 2{{\sin }^2}2x}}{{2\sin 2x\cos 2x}} = \mathop {\lim }\limits_{x \to 0} \frac{{ - \sin 2x}}{{\cos 2x}} = 0\).

4) Tính giới hạn \(A = \mathop {\lim }\limits_{x \to 0} \frac{{1 - \sin 2x - \cos 2x}}{{1 + \sin 2x - \cos 2x}}\).

Giải:

\(A = \mathop {\lim }\limits_{x \to 0} \frac{{1 - \sin 2x - \cos 2x}}{{1 + \sin 2x - \cos 2x}} = \mathop {\lim }\limits_{x \to 0} \frac{{1 - 2\sin x\cos x - ({{\cos }^2}x - {{\sin }^2}x)}}{{1 + 2\sin x\cos x - ({{\cos }^2}x - {{\sin }^2}x)}}\)

\( = \mathop {\lim }\limits_{x \to 0} \frac{{2{{\sin }^2}x - 2\sin x\cos x}}{{2{{\sin }^2}x + 2\sin x\cos x}} = \mathop {\lim }\limits_{x \to 0} \frac{{2\sin x(\sin x - \cos x)}}{{2\sin x(\sin x + \cos x)}} = \mathop {\lim }\limits_{x \to 0} \frac{{\sin x - \cos x}}{{\sin x + \cos x}} =  - 1\).