Cách xét tính liên tục của hàm số tại một điểm, trên tập xác định - Toán 11

a) Phương pháp giải:

Hàm số liên tục tại điểm \(x = {x_0}\) khi \(f({x_0}) = \mathop {\lim }\limits_{x \to {x_0}} f(x)\) hoặc \(f({x_0}) = \mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = \mathop {\lim }\limits_{x \to {x_0}^ - } f(x)\).

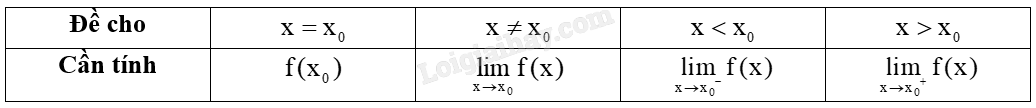
b) Ví dụ minh hoạ:

1) Xét tính liên tục của hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{\frac{{{x^2} - 3x + 2}}{{x - 2}}}&{khi}&{x \ne 2}\\{4x - 7}&{khi}&{x = 2}\end{array}} \right.\) tại điểm \({x_0} = 2\).

Giải:

Ta có \(f({x_0}) = f(2) = 4 \cdot 2 - 7 = 1\).

\(\mathop {\lim }\limits_{x \to 2} f(x) = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 3x + 2}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{(x - 2)(x - 1)}}{{x - 2}} = 1\).

Suy ra \(f(2) = \mathop {\lim }\limits_{x \to 2} f(x)\) nên hàm số \(f(x)\) liên tục tại điểm \({x_0} = 2\).

2) Xét tính liên tục của hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{{x^2} - 3x + 3}&{khi}&{x \le 2}\\{\frac{{1 - \sqrt {2x - 3} }}{{2 - x}}}&{khi}&{x > 2}\end{array}} \right.\) tại điểm \({x_0} = 2\).

Giải:

Ta có \(f({x_0}) = f(2) = {2^2} - 3.2 + 3 = 1\).

\(\mathop {\lim }\limits_{x \to {2^ - }} f(x) = \mathop {\lim }\limits_{x \to {2^ - }} ({x^2} - 3x + 3) = 1\).

\(\mathop {\lim }\limits_{x \to {2^ + }} f(x) = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{1 - \sqrt {2x - 3} }}{{2 - x}} = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{1 - 2x + 3}}{{(2 - x)(1 + \sqrt {2x - 3} )}} = \mathop {\lim }\limits_{x \to {2^ + }} \frac{2}{{1 + \sqrt {2x - 3} }} = 1\).

Suy ra \(f(2) = \mathop {\lim }\limits_{x \to {2^ - }} f(x) = \mathop {\lim }\limits_{x \to {2^ + }} f(x)\) nên hàm số \(f(x)\) liên tục tại điểm \({x_0} = 2\).

3) Xét tính liên tục của hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{\frac{{{x^2} - 9}}{{\sqrt {x + 1}  - 2}}}&{khi}&{x > 3}\\{2x + 12}&{khi}&{x \le 3}\end{array}} \right.\) tại điểm \({x_0} = 3\).

Giải:

Ta có \(f({x_0}) = f(3) = 18\).

\(\mathop {\lim }\limits_{x \to {3^ - }} f(x) = \mathop {\lim }\limits_{x \to {3^ - }} (2x + 12) = 18\).

\(\mathop {\lim }\limits_{x \to {3^ + }} f(x) = \mathop {\lim }\limits_{x \to {3^ + }} \frac{{{x^2} - 9}}{{\sqrt {x + 1}  - 2}} = \mathop {\lim }\limits_{x \to {3^ + }} \frac{{(x - 3)(x + 3)(\sqrt {x + 1}  + 2)}}{{x - 3}}\)

\( = \mathop {\lim }\limits_{x \to {3^ + }} (x + 3)(\sqrt {x + 1}  + 2) = 24\).

Suy ra \(f(3) = \mathop {\lim }\limits_{x \to {3^ - }} f(x) \ne \mathop {\lim }\limits_{x \to {3^ + }} f(x)\) nên hàm số \(f(x)\) không liên tục tại điểm \({x_0} = 3\).

4) Xét tính liên tục của hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{\frac{{x + 1 - \sqrt {x + 3} }}{{x - 1}}}&{khi}&{x > 1}\\{\frac{3}{4}}&{khi}&{x = 1}\\{\frac{{3{x^3} - 6{x^2} - 3x + 6}}{{3{x^2} - 14x + 11}}}&{khi}&{x < 1}\end{array}} \right.\) tại điểm \({x_0} = 1\).

Giải:

Ta có \(f({x_0}) = f(1) = \frac{3}{4}\).

\(\mathop {\lim }\limits_{x \to {1^ - }} f(x) = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{3{x^3} - 6{x^2} - 3x + 6}}{{3{x^2} - 14x + 11}} = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{(x - 1)(3{x^2} - 3x - 6)}}{{(x - 1)(3x - 11)}} = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{3{x^2} - 3x - 6}}{{3x - 11}} = \frac{3}{4}\)

\(\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{x + 1 - \sqrt {x + 3} }}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{{(x - 1)}^2} - (x + 3)}}{{(x - 1)(x + 1 + \sqrt {x + 3} )}} = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{x + 2}}{{x + 1 + \sqrt {x + 3} }} = \frac{3}{4}\).

Suy ra \(f(1) = \mathop {\lim }\limits_{x \to {1^ - }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} f(x)\) nên hàm số \(f(x)\) liên tục tại điểm \({x_0} = 1\).

5) Tìm a để hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{\frac{{{x^3} + 2{x^2} - 5x - 6}}{{{x^3} - 4x}}}&{khi}&{x \ne 2}\\{\frac{1}{8}(a + x)}&{khi}&{x = 2}\end{array}} \right.\) liên tục tại điểm \({x_0} = 2\).

Giải:

Ta có \(f(2) = \frac{1}{8}(a + 2)\).

\(\mathop {\lim }\limits_{x \to 2} f(x) = \mathop {\lim }\limits_{x \to 2} \frac{{{x^3} + 2{x^2} - 5x - 6}}{{{x^3} - 4x}} = \mathop {\lim }\limits_{x \to 2} \frac{{(x - 2)({x^2} + 4x + 3)}}{{x(x - 2)(x + 2)}} = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} + 4x + 3}}{{x(x + 2)}} = \frac{{15}}{8}\).

Hàm số liên tục tại điểm \({x_0} = 2 \Leftrightarrow f(2) = \mathop {\lim }\limits_{x \to 2} f(x) \Leftrightarrow \frac{1}{8}(a + 2) = \frac{{15}}{8} \Leftrightarrow a = 13\).

a) Phương pháp giải:

Hàm số liên tục tại điểm \(x = {x_0}\) khi \(f({x_0}) = \mathop {\lim }\limits_{x \to {x_0}} f(x)\) hoặc \(f({x_0}) = \mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = \mathop {\lim }\limits_{x \to {x_0}^ - } f(x)\).

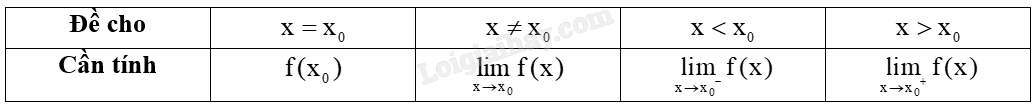
b) Ví dụ minh hoạ:

1) Xét tính liên tục của hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{\frac{{2{x^3} + x + 3}}{{{x^3} + 1}}}&{khi}&{x \ne  - 1}\\{\frac{7}{3}}&{khi}&{x =  - 1}\end{array}} \right.\) trên \(\mathbb{R}\).

Giải:

Xét \(x \ne  - 1\) thì \(f(x) = \frac{{2{x^3} + x + 3}}{{{x^3} + 1}}\) là hàm phân thức hữu tỉ nên liên tục trên các khoảng \(( - \infty ; - 1)\) và \(( - 1; + \infty )\) mà nó xác định.

Xét tính liên tục của hàm số \(f(x)\) tại \(x =  - 1\):

\(\mathop {\lim }\limits_{x \to  - 1} f(x) = \mathop {\lim }\limits_{x \to  - 1} \frac{{2{x^3} + x + 3}}{{{x^3} + 1}} = \mathop {\lim }\limits_{x \to  - 1} \frac{{(x + 1)(2{x^2} - 2x + 3)}}{{(x + 1)({x^2} - x + 1)}} = \mathop {\lim }\limits_{x \to  - 1} \frac{{2{x^2} - 2x + 3}}{{{x^2} - x + 1}} = \frac{7}{3}\).

\(f( - 1) = \frac{7}{3}\).

Suy ra \(\mathop {\lim }\limits_{x \to  - 1} f(x) = f( - 1)\) nên hàm số đã cho liên tục tại \({x_0} =  - 1\).

Vậy hàm số đã cho liên tục trên \(\mathbb{R}\).

2) Xét tính liên tục của hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{\frac{{{x^2} - 4x + 3}}{{x - 1}}}&{khi}&{x > 1}\\{\sqrt {5 - x} }&{khi}&{x \le 1}\end{array}} \right.\) trên \(\mathbb{R}\).

Giải:

Tập xác định của hàm số là \(D = \mathbb{R}\).

Với mọi \({x_0} \in (1; + \infty )\), \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^2} - 4x + 3}}{{x - 1}} = f({x_0})\). Suy ra hàm số đã cho liên tục trên khoảng \((1; + \infty )\).

Với mọi \({x_0} \in ( - \infty ;1)\), ta có \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = \mathop {\lim }\limits_{x \to {x_0}} \left( { - \sqrt {5 - x} } \right) =  - \sqrt {5 - {x_0}}  = f({x_0})\). Suy ra hàm số đã cho liên tục trên khoảng \(( - \infty ;1)\).

Xét tính liên tục của hàm số tại \(x = 1\):

\(f(1) =  - \sqrt {5 - 1}  = 2\).

\(\mathop {\lim }\limits_{x \to {1^ - }} f(x) = \mathop {\lim }\limits_{x \to {1^ - }} \left( { - \sqrt {5 - x} } \right) =  - 2\).

\(\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{(x - 1)(x - 3)}}{{x - 1}} = \mathop {\lim }\limits_{x \to {1^ + }} (x - 3) =  - 2\).

Suy ra \(\mathop {\lim }\limits_{x \to {1^ - }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} f(x) = f(1)\) nên hàm số đã cho liên tục tại \(x = 1\).

Vậy hàm số đã cho liên tục trên \(\mathbb{R}\).