 Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
 Bài 3. Hệ trục tọa độ trong không gian - Toán 12 Cùng k..
Bài 3. Hệ trục tọa độ trong không gian - Toán 12 Cùng k..
Giải mục 3 trang 70, 71, 72 SGK Toán 12 tập 1 - Cùng khám phá
Trong không gian Oxyz, cho vectơ (vec a). a) Xác định điểm M sao cho (overrightarrow {OM} = vec a). b) Gọi (left( {x;y;z} right)) là toạ độ của điểm M. Hãy biểu diễn (vec a) theo ba vectơ đơn vị (vec i,vec j,vec k).
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 70 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho vectơ \(\vec a\).
a) Xác định điểm M sao cho \(\overrightarrow {OM} = \vec a\).
b) Gọi \(\left( {x;y;z} \right)\) là toạ độ của điểm M. Hãy biểu diễn \(\vec a\) theo ba vectơ đơn vị \(\vec i,\vec j,\vec k\).
Phương pháp giải:
- Giả sử vectơ \(\vec a\) có tọa độ \(({a_1},{a_2},{a_3})\). Điểm \(M\) cần tìm sẽ có tọa độ \(({a_1},{a_2},{a_3})\) để thỏa mãn \(\overrightarrow {OM} = \vec a\).
- Biểu diễn của \(\overrightarrow a \) sẽ giống như biểu diễn \(\overrightarrow {OM} \).
Lời giải chi tiết:
a) Xác định điểm M:
- Vector \(\overrightarrow {OM} \) là vector có điểm đầu tại gốc tọa độ \(O(0,0,0)\) và điểm cuối tại điểm \(M(x,y,z)\). Do đó, \(\overrightarrow {OM} \) có dạng:
\(\overrightarrow {OM} = \overrightarrow {OM} = (x - 0)\vec i + (y - 0)\vec j + (z - 0)\vec k = x\vec i + y\vec j + z\overrightarrow k \)
- Nếu \(\overrightarrow {OM} = \vec a\), thì tọa độ của điểm M chính là các thành phần của vector \(\vec a\). Giả sử vector \(\vec a\) có dạng \(\vec a = \left( {{a_1},{a_2},{a_3}} \right)\), thì: \(M\left( {{a_1},{a_2},{a_3}} \right)\)
- Như vậy, điểm M có tọa độ \(\left( {{a_1},{a_2},{a_3}} \right)\)
b) Biểu diễn \(\vec a\) theo các vector đơn vị \(\vec i,\vec j,\vec k\)
- Gọi \((x,y,z)\) là tọa độ của điểm M. Như đã phân tích ở phần a, vector \(\overrightarrow {OM} \) có dạng: \(\overrightarrow {OM} = x\vec i + y\vec j + z\vec k\)
- Do \(\overrightarrow {OM} = \vec a\), ta có: \(\vec a = x\vec i + y\vec j + z\vec k\)
- Như vậy vector \(\vec a\) có thể biểu diễn theo các vector đơn vị \(\vec i,\vec j,\vec k\) dưới dạng:
\(\vec a = {a_1}\vec i + {a_2}\vec j + {a_3}\vec k\)
LT4
Trả lời câu hỏi Luyện tập 4 trang 71 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho ba vectơ \(\vec a = \left( { - 1;0;3} \right),\vec b = \left( {2;1;0} \right),\vec c = \left( { - 2;3;5} \right)\). Tìm toạ độ của \(\vec x = 2\vec a - \frac{1}{2}\vec b - 3\vec c\).
Phương pháp giải:
Tính toán các thành phần của vectơ đã cho rồi cộng chúng lại.
Lời giải chi tiết:
Tính toán từng vectơ thành phần của \(\vec x\):\(2\vec a = 2 \times \left( { - 1,0,3} \right) = \left( { - 2,0,6} \right), - \frac{1}{2}\vec b = - \frac{1}{2} \times \left( {2,1,0} \right) = \left( { - 1, - \frac{1}{2},0} \right), - 3\vec c = - 3 \times \left( { - 2,3,5} \right) = \left( {6, - 9, - 15} \right).\)
Cộng các vectơ thành phần để tìm tọa độ của \(\vec x\):
\(\vec x = \left( { - 2,0,6} \right) + \left( { - 1, - \frac{1}{2},0} \right) + \left( {6, - 9, - 15} \right)\).
Tọa độ của \(\vec x\) là:
\(x = - 2 - 1 + 6 = 3,y = 0 - \frac{1}{2} - 9 = - \frac{{19}}{2},z = 6 + 0 - 15 = - 9.\)
Vậy, tọa độ của vectơ \(\vec x\) là \(\left( {3, - \frac{{19}}{2}, - 9} \right)\).
HĐ4
Trả lời câu hỏi Hoạt động 4 trang 71 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho hai điểm \(M({x_M},{y_M},{z_M})\) và \(N({x_N},{y_N},{z_N})\) (Hình 2.36).
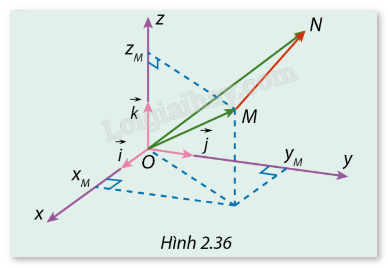
a) Biểu diễn \(\overrightarrow {MN} \) qua các vectơ \(\overrightarrow {OM} \) và \(\overrightarrow {ON} \).
b) Biểu diễn mỗi vectơ \(\overrightarrow {OM} \), \(\overrightarrow {ON} \) qua các vectơ đơn vị \(\vec i\), \(\vec j\), \(\vec k\).
c) Chứng minh rằng \(\overrightarrow {MN} = ({x_N} - {x_M})\vec i + ({y_N} - {y_M})\vec j + ({z_N} - {z_M})\vec k\).
Phương pháp giải:
- Sử dụng định nghĩa và tính chất của vectơ trong không gian.
- Sử dụng biểu thức của vectơ trong hệ tọa độ Oxyz qua các vectơ đơn vị \(\vec i\), \(\vec j\),\(\vec k\).
Lời giải chi tiết:
a) Biểu diễn \(\overrightarrow {MN} \) qua các vectơ \(\overrightarrow {OM} \) và \(\overrightarrow {ON} \):
Ta có: \(\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} \)
b) Biểu diễn mỗi vectơ \(\overrightarrow {OM} \), \(\overrightarrow {ON} \) qua các vectơ đơn vị \(\vec i\), \(\vec j\), \(\vec k\):
Với các tọa độ đã cho:
\(\overrightarrow {OM} = {x_M}\vec i + {y_M}\vec j + {z_M}\vec k\)
\(\overrightarrow {ON} = {x_N}\vec i + {y_N}\vec j + {z_N}\vec k\)
c) Chứng minh rằng \(\overrightarrow {MN} = ({x_N} - {x_M})\vec i + ({y_N} - {y_M})\vec j + ({z_N} - {z_M})\vec k\):
Dùng kết quả của phần (a) và (b): \(\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} = ({x_N}\vec i + {y_N}\vec j + {z_N}\vec k) - ({x_M}\vec i + {y_M}\vec j + {z_M}\vec k)\)
Kết quả:
\(\overrightarrow {MN} = ({x_N} - {x_M})\vec i + ({y_N} - {y_M})\vec j + ({z_N} - {z_M})\vec k\)
LT5
Trả lời câu hỏi Luyện tập 5 trang 72 SGK Toán 12 Cùng khám phá
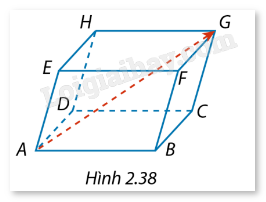
Trong không gian Oxyz, cho hình hộp ABCD.EFGH có A(1; 0; -1), B(2; 1; 3) và H(4; 3; 4) (Hình 2.38).
a) Tìm tọa độ của đỉnh G.
b) Tìm tọa độ của \(\overrightarrow {AG} \).
Phương pháp giải:
- Sử dụng các tính chất của hình hộp chữ nhật trong không gian, đặc biệt là các quy tắc liên quan đến tọa độ của các đỉnh dựa trên tính chất đối xứng và các đường chéo.
- Áp dụng công thức sau để tính toạ độ vectơ trong không gian.
\(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = \left( {{x_B} - {x_A},{y_B} - {y_A},{z_B} - {z_A}} \right)\)
Lời giải chi tiết:
a) Tìm toạ độ của điểm G
Vì ABCD.EFGH là một hình hộp, nên G là đỉnh đối diện với A và \(\overrightarrow {HG} = \overrightarrow {AB} \).
Mà \(\overrightarrow {HG} = \overrightarrow {OG} - \overrightarrow {OH} \) nên suy ra \(\overrightarrow {OG} = \overrightarrow {AB} + \overrightarrow {OH} \)
Do đó, tọa độ của G được tính bằng cách lấy toạ độ của vectơ \(\overrightarrow {AB} \) cộng tọa độ của điểm H hay nói cách khác là lấy toạ độ của điểm B cộng với tọa độ của điểm H trừ đi tọa độ của điểm A: \(G = B + H - A\)
Tính toán cụ thể: \(G = (2,1,3) + (4,3,4) - (1,0, - 1) = (5,4,8)\)
Vậy tọa độ của điểm \(G\) là \((5,4,8)\).
b) Tìm tọa độ của \(\overrightarrow {AG} \):
Tọa độ của vectơ \(\overrightarrow {AG} \) được tính bằng tọa độ của G trừ tọa độ của A:
\(\overrightarrow {AG} = ({x_G} - {x_A},{y_G} - {y_A},{z_G} - {z_A})\)
Thay các giá trị đã biết: \(\overrightarrow {AG} = (5 - 1,4 - 0,8 - ( - 1)) = (4,4,9)\)
Vậy tọa độ của \(\overrightarrow {AG} \) là \((4,4,9)\).
VD
Trả lời câu hỏi Vận dụng trang 72 SGK Toán 12 Cùng khám phá
Trong không gian \(Oxyz,\),một vật đi từ điểm \(A(2;3;0)\) đến điểm \(B( - 1;1;2)\) rồi tiếp tục đi đến điểm \(C(3; - 2; - 1)\). Tìm vectơ biểu thị độ dịch chuyển của vật khi:
a) Vật đi từ điểm \(A\) đến điểm \(B\);
b) Vật đi từ điểm \(A\) đến điểm \(C\).
Phương pháp giải:
- Để tìm vectơ biểu thị độ dịch chuyển của vật, ta sử dụng công thức tính vectơ từ một điểm này đến một điểm khác trong không gian ba chiều.
- Vectơ độ dịch chuyển từ điểm \(A\) đến điểm \(B\) được tính bằng tọa độ điểm \(B\) trừ đi tọa độ điểm \(A\).
- Tương tự, vectơ độ dịch chuyển từ điểm \(A\) đến điểm \(C\) được tính bằng tọa độ điểm \(C\) trừ đi tọa độ điểm \(A\).
Lời giải chi tiết:
a) Vectơ độ dịch chuyển của vật khi đi từ \(A\) đến \(B\):
Vectơ \(\overrightarrow {AB} \) được tính bằng công thức:
\(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})\)
Thay các giá trị đã biết: \(\overrightarrow {AB} = ( - 1 - 2;1 - 3;2 - 0) = ( - 3; - 2;2)\)
Vậy vectơ độ dịch chuyển từ \(A\) đến \(B\) là \(\overrightarrow {AB} = ( - 3; - 2;2)\).
b) Vectơ độ dịch chuyển của vật khi đi từ \(A\) đến \(C\):
Vectơ \(\overrightarrow {AC} \) được tính bằng công thức:
\(\overrightarrow {AC} = ({x_C} - {x_A};{y_C} - {y_A};{z_C} - {z_A})\)
Thay các giá trị đã biết: \(\overrightarrow {AC} = (3 - 2; - 2 - 3; - 1 - 0) = (1; - 5; - 1)\)
Vậy vectơ độ dịch chuyển từ \(A\) đến \(C\) là \(\overrightarrow {AC} = (1; - 5; - 1)\).
- Giải bài tập 2.13 trang 73 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 2.14 trang 73 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 2.15 trang 73 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 2.16 trang 73 SGK Toán 12 tập 1 - Cùng khám phá
- Giải mục 2 trang 68, 69, 70 SGK Toán 12 tập 1 - Cùng khám phá
>> Xem thêm
Các bài khác cùng chuyên mục
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá












Danh sách bình luận