 Toán 8, giải toán lớp 8 kết nối tri thức với cuộc sống
Toán 8, giải toán lớp 8 kết nối tri thức với cuộc sống
 Bài 11. Hình thang cân Toán 8 kết nối tri thức
Bài 11. Hình thang cân Toán 8 kết nối tri thức
Giải mục 2 trang 53, 54 SGK Toán 8 tập 1 - Kết nối tri thức
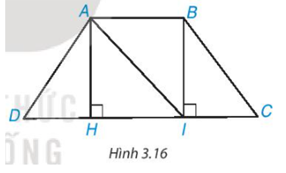
Cho hình thang cân ABCD, AC // CD và AB < CD (H.3.16).
HĐ1
Video hướng dẫn giải
Cho hình thang cân ABCD, AC // CD và AB < CD (H.3.16).
a) Từ A và B kẻ AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD. Chứng minh rằng AH = BI bằng cách chứng minh ∆AHI = ∆IBA.
b) Chứng minh ∆AHD = ∆BIC, từ đó suy ra AD = BC
Phương pháp giải:
a) Chứng minh: ∆AHI = ∆IBA (g.c.g).
Suy ra AH = BI (hai cạnh tương ứng).
b) Chứng minh: ∆AHD = ∆BIC (góc - góc).
Suy ra AD = BC (hai cạnh tương ứng).
Lời giải chi tiết:
a) Vì ABCD là hình thang cân (AB // CD) nên \(\widehat {BAI} = \widehat {AIH}\) (hai góc so le trong).
Ta có AH ⊥ DC, BI ⊥ DC suy ra AH // BI.
Do đó \(\widehat {AIB} = \widehat {HAI}\) (hai góc so le trong).
Xét ∆AHI và ∆IBA có:
\(\widehat {BAI} = \widehat {AIH}\) (chứng minh trên);
Cạnh AI chung;
\(\widehat {AIB} = \widehat {HAI}\) (hai góc so le trong).
Do đó ∆AHI = ∆IBA (g.c.g).
Suy ra AH = BI (hai cạnh tương ứng).
b) Vì ABCD là hình thang cân (AB // CD) nên \(\widehat C = \widehat D\).
Vì ∆AHD và ∆BIC có:
\(\widehat {AH{\rm{D}}} = \widehat {BIC} = {90^o}\) và \(\widehat C = \widehat D\) nên \(90^o - \widehat C = 90^o - \widehat {BIC} \Leftrightarrow \widehat {DAH} = \widehat {CBI}\)
Xét ∆AHD và ∆BIC có:
\(\widehat {AH{\rm{D}}} = \widehat {BIC} = {90^o}\) (vì AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD);
\(AH = BI\) (chứng minh trên
\(\widehat {DAH} = \widehat {CBI}\) (chứng minh trên).
Do đó ∆AHD = ∆BIC (góc - cạnh - góc).
Suy ra AD = BC (hai cạnh tương ứng).
LT 2
Video hướng dẫn giải
Cho tứ giác ABCD như Hình 3.18. Biết rằng \(\widehat A = \widehat B = \widehat {{D_1}}\). Chứng minh rằng AD = BC.
Phương pháp giải:
Chứng minh ABCD là hình thang có \(\widehat A = \widehat B\)
Lời giải chi tiết:
Ta có \(\widehat A = \widehat {{D_1}}\) mà hai góc này ở vị trí đồng vị nên AB // CD.
Suy ra tứ giác ABCD là hình thang.
Mặt khác hình thang ABCD có \(\widehat A = \widehat B\) nên ABCD là hình thang cân.
Do đó AD = BC (đpcm).
HĐ2
Video hướng dẫn giải
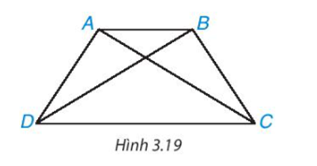
Cho hình thang cân ABCD, kẻ hai đường chéo AC, BD (H.3.19). Hãy chứng minh ∆ACD = ∆BDC. Từ đó suy ra AC = BD
Phương pháp giải:
Chứng minh: ∆ACD = ∆BDC (c.g.c).
Suy ra AC = BD (hai góc tương ứng).
Lời giải chi tiết:
Vì ABCD là hình thang cân (AC // CD) nên AD = BC; \(\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}}\)
Xét ∆ACD và ∆BDC có
AD = BC (chứng minh trên);
\(\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}}\) (chứng minh trên);
Cạnh CD chung.
Do đó ∆ACD = ∆BDC (c.g.c).
Suy ra AC = BD (hai góc tương ứng).
LT 3
Video hướng dẫn giải
Cho tam giác ABC cân tại A. Kẻ một đường thẳng d song song với BC, d cắt cạnh AB tại D và cắt cạnh AC tại E (H.3.20).
a) Tứ giác DECB là hình gì?
b) Chứng minh BE = CD.
Phương pháp giải:
Sử dụng tính chất của hình thang cân.
Lời giải chi tiết:
a) Theo đề bài: d // BC nên DE // BC
Suy ra DECB là hình thang.
Vì tam giác ABC cân tại A nên \(\widehat B = \widehat C\).
Hình thang DECB có \(\widehat B = \widehat C\) nên tứ giác DECB là hình thang cân.
b) Hình thang cân DECB có BE và CD là hai đường chéo.
Do đó BE = CD (đpcm).
- Giải mục 3 trang 54, 55 SGK Toán 8 tập 1 - Kết nối tri thức
- Giải bài 3.4 trang 55 SGK Toán 8 tập 1 - Kết nối tri thức
- Giải bài 3.5 trang 55 SGK Toán 8 tập 1 - Kết nối tri thức
- Giải bài 3.6 trang 55 SGK Toán 8 tập 1 - Kết nối tri thức
- Giải bài 3.7 trang 55 SGK Toán 8 tập 1 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Giải dự án 2 trang 112 SGK Toán 8 tập 1
- Lý thuyết Hình chóp tứ giác đều SGK Toán 8 - Kết nối tri thức
- Lý thuyết Hình chóp tam giác đều SGK Toán 8 - Kết nối tri thức
- Lý thuyết Hình đồng dạng SGK Toán 8 - Kết nối tri thức
- Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông SGK Toán 8 - Kết nối tri thức














Danh sách bình luận