 Giải chuyên đề học tập Toán lớp 11 Chân trời sáng tạo
Giải chuyên đề học tập Toán lớp 11 Chân trời sáng tạo
 Bài 4. Phép đối xứng tâm Chuyên đề học tập Toán 11 Chân..
Bài 4. Phép đối xứng tâm Chuyên đề học tập Toán 11 Chân..
Giải mục 2 trang 21, 22 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Giả sử ĐO là phép đối xứng tâm O. Lấy hai điểm tùy ý A, B sao cho ba điểm O, A, B không thẳng hàng.
Khám phá 2
Giả sử ĐO là phép đối xứng tâm O. Lấy hai điểm tùy ý A, B sao cho ba điểm O, A, B không thẳng hàng. Gọi A’, B’ lần lượt là ảnh của A, B qua ĐO. So sánh tam giác OAB và tam giác O’A’B’ rồi so sánh A’B’ và AB.
Phương pháp giải:
Vẽ hình sau đó quan sát và so sánh
Lời giải chi tiết:

Theo đề, ta có \({Đ_O}\left( A \right){\rm{ }} = {\rm{ }}A'.\)
Suy ra O là trung điểm AA’, do đó \(OA{\rm{ }} = {\rm{ }}OA'.\)
Chứng minh tương tự, ta được \(OB{\rm{ }} = {\rm{ }}OB'.\)
Xét \(\Delta OAB\) và \(\Delta OA'B'\), có:
\(OA{\rm{ }} = {\rm{ }}OA'\) (chứng minh trên);
\(\widehat {AOB} = \widehat {A'OB'}\) (đối đỉnh);
\(OB{\rm{ }} = {\rm{ }}OB'\) (chứng minh trên).
Do đó \(\Delta OAB{\rm{ }} = {\rm{ }}\Delta OA'B'{\rm{ }}\left( {c.g.c} \right).\)
Suy ra \(A'B'{\rm{ }} = {\rm{ }}AB\) (cặp cạnh tương ứng).
Vậy \(\Delta OAB{\rm{ }} = {\rm{ }}\Delta OA'B'{\rm{ }}\) và \(A'B'{\rm{ }} = {\rm{ }}AB.\)
Thực hành 2
Trong mặt phẳng tọa độ Oxy, tìm ảnh qua ĐO của
a) điểm M(3; –4);
b) đường thẳng d: x – 3y + 6 = 0;
c) đường tròn (C): (x + 2)2 + (y – 1)2 = 4.
Phương pháp giải:
Nếu \(M'{\rm{ }} = {\rm{ }}{Đ_I}\left( M \right)\) thì \(\left\{ \begin{array}{l}{x_{M'}} + {x_M} = 2{x_I}\\{y_{M'}} + {y_M} = 2{y_I}\end{array} \right.\) (I là trung điểm của MM’)
Lời giải chi tiết:
a) Gọi M’ là ảnh của M qua ĐO.
Suy ra O là trung điểm của MM’ với \(M\left( {3;{\rm{ }}-4} \right).\)
Do đó \(\left\{ \begin{array}{l}{x_{M'}} = 2{x_O} - {x_M} = 2.0 - 3 = - 3\\{y_{M'}} = 2{y_O} - {y_M} = 2.0 + 4 = 4\end{array} \right.\)
Vậy \(M'\left( {-3;{\rm{ }}4} \right).\)
b) • Chọn \(A\left( {0;{\rm{ }}2} \right) \in d:{\rm{ }}x{\rm{ }}-{\rm{ }}3y{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}0.\)
Gọi A’là ảnh của A qua \({Đ_O}.\)
Suy ra O là trung điểm của AA’ với A(0; 2)
Do đó \(\left\{ \begin{array}{l}{x_{A'}} = 2{x_O} - {x_A} = 2.0 - 0 = 0\\{y_{A'}} = 2{y_O} - {y_A} = 2.0 - 2 = - 2\end{array} \right.\)
Vì vậy A’(0; –2).
• Đường thẳng \(d:{\rm{ }}x{\rm{ }}-{\rm{ }}3y{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}0\) có vectơ pháp tuyến \({\rm{\vec n}} = \left( {1; - 3} \right)\)
Gọi d’ là ảnh của d qua \({Đ_O}.\)
Suy ra d’ song song hoặc trùng với d, nên d’ nhận vectơ pháp tuyến của d là \({\rm{\vec n}} = \left( {1; - 3} \right)\) làm vectơ pháp tuyến.
Vậy đường thẳng d’ đi qua A’(0; –2) và nhận làm vectơ \({\rm{\vec n}} = \left( {1; - 3} \right)\) pháp tuyến nên có phương trình là:
\(1\left( {x{\rm{ }}-{\rm{ }}0} \right){\rm{ }}-{\rm{ }}3\left( {y{\rm{ }} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }}0 \Leftrightarrow x-3y-6 = 0.\)
c) Đường tròn \(\left( C \right):{\rm{ }}{\left( {x{\rm{ }} + {\rm{ }}2} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}1} \right)^2}\; = {\rm{ }}4\) có tâm I(–2; 1), bán kính R = 2.
Gọi (C’) là ảnh của (C) qua ĐO nên (C’) có tâm là ảnh của I(–2; 1) và có bán kính R’ = R = 2.
Gọi I’= ĐO(I).
Suy ra O là trung điểm \(II'.\)
Do đó \(\left\{ \begin{array}{l}{x_{I'}} = 2{x_O} - {x_I} = 2.0 + 2 = 2\\{y_{I'}} = 2{y_O} - {y_I} = 2.0 - 1 = - 1\end{array} \right.\)
Vì vậy tọa độ I’(2; –1).
Vậy đường tròn (C’) là ảnh của (C) qua ĐO, có tâm I’(2; –1) và R’ = 2 nên có phương trình là:
\({\left( {x{\rm{ }}-{\rm{ }}2} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }} + {\rm{ }}1} \right)^2}\; = {\rm{ }}4.\)
Vận dụng 2
Trong Hình 6, tìm các số ghi tại điểm đối xứng qua tâm bia với điểm ghi các số 20; 7; 9.
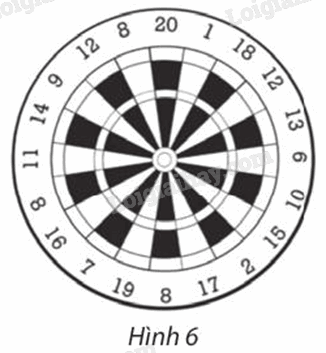
Phương pháp giải:
Quan sát hình 6 để tìm
Lời giải chi tiết:
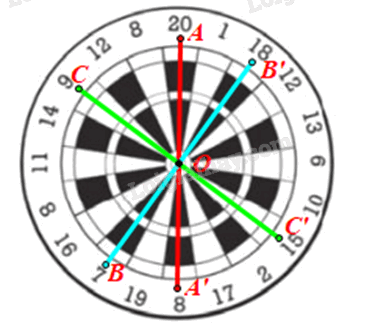
Gọi O là tâm bia.
• Lấy điểm A nằm trong ô có điểm ghi số 20. Lấy A’ đối xứng với A qua O.
Khi đó ta được điểm A’ nằm trong ô có điểm ghi số 8.
• Lấy điểm B nằm trong ô có điểm ghi số 7. Lấy B’ đối xứng với B qua O.
Khi đó ta được điểm B’ nằm trong ô có điểm ghi số 18.
• Lấy điểm C nằm trong ô có điểm ghi số 9. Lấy C’ đối xứng với C qua O.
Khi đó ta được điểm C’ nằm trong ô có điểm ghi số 15.
Vậy điểm đối xứng qua tâm bia với điểm ghi các số 20; 7; 9 lần lượt là 8; 18; 15.
- Giải mục 3 trang 22, 23 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
- Giải bài 1 trang 24 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 2 trang 24 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 3 trang 24 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 4 trang 24 Chuyên đề học tập Toán 11 Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải mục 2 trang 84, 85 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
- Giải bài 3 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 11 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 12 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 10 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải mục 2 trang 84, 85 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
- Giải bài 3 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 12 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 11 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 10 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo












Danh sách bình luận