Giải mục 1 trang 97, 98, 99, 100 SGK Toán 12 tập 2 - Cánh diều

MĐ

Trả lời câu hỏi Bài toán mở đầu trang 97 SGK Toán 12 Cánh diều

Dây chuyền lắp ráp ô tô điện gồm các linh kiện là sản phẩm do hai nhà máy sản xuất ra. Số linh kiện nhà máy I sản xuất ra chiếm 55% tổng số linh kiện, số linh kiện nhà máy II sản xuất ra chiếm 45% tổng số linh kiện; tỉ lệ linh kiện đạt tiêu chuẩn của nhà máy I là 90%, của nhà máy II là 87%. Lấy ra ngẫu nhiên một linh kiện từ dây chuyền lắp ráp đó để kiểm tra. Xác suất để linh kiện được lấy ra đạt tiêu chuẩn là bao nhiêu?

Phương pháp giải:

Sử dụng kiến thức về công thức xác suất toàn phần để tính: Cho hai biến cố A và B với \(0 < P\left( B \right) < 1\), ta có \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).

Lời giải chi tiết:

Gọi A là biến cố: “Linh kiện lấy ra đạt tiêu chuẩn”, B là biến cố: “Linh kiện lấy ra do nhà máy I sản xuất”. Khi đó, \(P\left( B \right) = 0,55;P\left( {\overline B } \right) = 0,45,P\left( {A|B} \right) = 0,9,P\left( {A|\overline B } \right) = 0,87\)

Theo công thức xác suất toàn phần ta có:

\(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right) = 0,55.0,9 + 0,45.0,87 = 0,8865\).

Vậy xác suất để linh kiện lấy ra đạt tiêu chuẩn là 0,8865.

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 97 SGK Toán 12 Cánh diều

Một hộp có 24 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 24; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biến cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố B: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”.

a) Viết các tập con của không gian mẫu tương ứng với các biến cố A, B, \(A \cap B,A \cap \overline B \) (Hình 2).

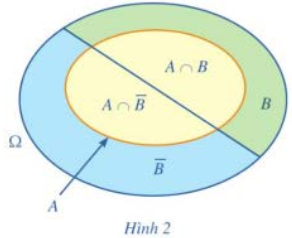
b) So sánh n(A) và \(n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right)\). Từ đó, hãy chứng tỏ rằng: \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right)\).

c) So sánh \(P\left( {A \cap B} \right)\) và \(P\left( B \right).P\left( {A|B} \right)\);

\(P\left( {A \cap \overline B } \right)\) và \(P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).

Từ đó, hãy chứng tỏ rằng: \(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).

Phương pháp giải:

+ Sử dụng kiến thức về định nghĩa xác suất có điều kiện để tính: Cho hai biến cố A và B. Xác suất của biến cố A với điều kiện biến cố B đã xảy ra được gọi là xác suất của A với điều kiện B, kí hiệu là P(A|B). Nếu \(P\left( B \right) > 0\) thì \(P\left( {A|B} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}}\).

+ Sử dụng kiến thức về công thức tính xác suất của hai biến cố xung khắc: Nếu A và B là hai biến cố xung khắc thì \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\).

Lời giải chi tiết:

a) \(A = \left\{ {3;{\rm{ }}6;{\rm{ }}9;{\rm{ }}12;{\rm{ }}15;{\rm{ }}18;{\rm{ }}21;{\rm{ }}24} \right\},B = \left\{ {4;{\rm{ }}8;{\rm{ }}12;{\rm{ }}16;{\rm{ }}20;{\rm{ }}24} \right\}\), \(\Omega  = \left\{ {1;2;3;...;24} \right\}\)\(A \cap B = \left\{ {12;24} \right\},A \cap \overline B  = \left\{ {3;6;9;15;18;21} \right\}\).

b) Ta có: \(n\left( A \right) = 8,n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right) = 2 + 6 = 8\) nên \(n\left( A \right) = n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right)\).

\(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \frac{{n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right)}}{{n\left( \Omega  \right)}} = \frac{{n\left( {A \cap B} \right)}}{{n\left( \Omega  \right)}} + \frac{{n\left( {A \cap \overline B } \right)}}{{n\left( \Omega  \right)}} = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right)\)

c) Ta có: \(P\left( B \right).P\left( {A|B} \right) = P\left( B \right).\frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}} = P\left( {A \cap B} \right)\);

\(P\left( {\overline B } \right).P\left( {A|\overline B } \right) = P\left( {\overline B } \right).\frac{{P\left( {A \cap \overline B } \right)}}{{P\left( {\overline B } \right)}} = P\left( {A \cap \overline B } \right)\).

Vì \(A \cap B,A \cap \overline B \) là hai biến cố xung khắc nên \(\left( {A \cap B} \right) \cup \left( {A \cap \overline B } \right) = A\), theo công thức xác suất ta có: \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).

LT1

Trả lời câu hỏi Luyện tập 1 trang 99 SGK Toán 12 Cánh diều

Hãy giải bài toán mở đầu bằng cách lập bảng thống kê như trong Ví dụ 2, biết rằng cả hai nhà máy sản xuất được 10 000 linh kiện.

Dây chuyền lắp ráp ô tô điện gồm các linh kiện là sản phẩm do hai nhà máy sản xuất ra. Số linh kiện nhà máy I sản xuất ra chiếm 55% tổng số linh kiện, số linh kiện nhà máy II sản xuất ra chiếm 45% tổng số linh kiện; tỉ lệ linh kiện đạt tiêu chuẩn của nhà máy I là 90%, của nhà máy II là 87%. Lấy ra ngẫu nhiên một linh kiện từ dây chuyền lắp ráp đó để kiểm tra.

Phương pháp giải:

Sử dụng kiến thức về công thức xác suất toàn phần để tính: Cho hai biến cố A và B với \(0 < P\left( B \right) < 1\), ta có \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).

Lời giải chi tiết:

Số linh kiện do nhà máy I sản xuất là: \(10\;000.55\%  = 5\;500\) (linh kiện).

Số linh kiện do nhà máy II sản xuất là: \(10\;000.45\%  = 4\;500\) (linh kiện).

Số linh do nhà máy I sản xuất đạt tiêu chuẩn là:

\(5\;500.90\%  = 4\;950\) (linh kiện).

Số linh do nhà máy I sản xuất không đạt tiêu chuẩn là: \(5\;500 - 4\;950 = 550\) (linh kiện).

Số linh do nhà máy II sản xuất đạt tiêu chuẩn là: \(4\;500.87\%  = 3\;915\) (linh kiện).

Số linh do nhà máy II sản xuất không đạt tiêu chuẩn là: \(4\;500 - 3\;915 = 585\) (linh kiện).

Ta có bảng thống kê như sau:

Gọi A là biến cố: “Linh kiện lấy ra đạt tiêu chuẩn”, B là biến cố: “Linh kiện lấy ra do nhà máy I sản xuất”. Khi đó, \(P\left( B \right) = 0,55;P\left( {\overline B } \right) = 0,45,P\left( {A|B} \right) = 0,9,P\left( {A|\overline B } \right) = 0,87\).

Theo công thức xác suất toàn phần ta có:

\(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right) = 0,55.0,9 + 0,45.0,87 = 0,8865\).

Vậy xác suất để linh kiện lấy ra đạt tiêu chuẩn là 0,8865.

LT2

Trả lời câu hỏi Luyện tập 2 trang 100 SGK Toán 12 Cánh diều

Hãy giải bài toán mở đầu bằng phương pháp sử dụng sơ đồ hình cây như trong Ví dụ 3.

Phương pháp giải:

+ Sử dụng kiến thức sơ đồ hình cây để tính.

 + Sử dụng kiến thức về công thức xác suất toàn phần để tính: Cho hai biến cố A và B với \(0 < P\left( B \right) < 1\), ta có \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {B|A} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).

Lời giải chi tiết:

Gọi A là biến cố: “Linh kiện lấy ra đạt tiêu chuẩn”, B là biến cố: “Linh kiện lấy ra do nhà máy I sản xuất”. Khi đó, \(P\left( B \right) = 0,55;P\left( {\overline B } \right) = 0,45,P\left( {A|B} \right) = 0,9,P\left( {A|\overline B } \right) = 0,87\)

Sơ đồ hình cây biểu thị tình huống đã cho:

p

Theo công thức xác suất toàn phần ta có:

\(P\left( A \right) = P\left( B \right).P\left( {B|A} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right) = 0,55.0,9 + 0,45.0,87 = 0,8865\).

Vậy xác suất để linh kiện lấy ra đạt tiêu chuẩn là 0,8865.