Giải mục 1 trang 79, 80 SGK Toán 12 tập 2 - Cánh diều
Hình 38 mô tả một mặt cầu trong không gian. Trong không gian với hệ tọa độ Oxyz, phương trình của mặt cầu được lập như thế nào?
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 79 SGK Toán 12 Cánh diều
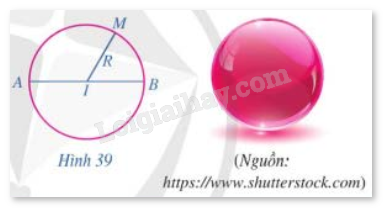
Nếu quay đường tròn tâm I bán kính R quanh đường kính AB một vòng (Hình 39) thì hình tạo thành được gọi là mặt cầu. Những điểm thuộc mặt cầu đó cách I một khoảng bằng bao nhiêu?
Phương pháp giải:
Khi quay đường tròn tâm I bán kính R quanh đường kính AB một vòng thì điểm thuộc mặt cầu đó cách I một khoảng bằng R.
Lời giải chi tiết:
Khi quay đường tròn tâm I bán kính R quanh đường kính AB một vòng thì điểm thuộc mặt cầu đó cách I một khoảng bằng R.
LT1
Trả lời câu hỏi Luyện tập 1 trang 80 SGK Toán 12 Cánh diều
Trong không gian với hệ tọa độ Oxyz, cho điểm I(1; 2; 3) và mặt cầu tâm I đi qua điểm A(0; 4; 5). Tính đường kính của mặt cầu đó.
Phương pháp giải:
Sử dụng kiến thức về vị trí của điểm so với mặt cầu để tìm bán kính của mặt cầu: Cho mặt cầu tâm I, bán kính R và điểm M bất kì trong không gian. Điểm M thuộc mặt cầu tâm I, bán kính R khi và chỉ khi \(IM = R\).
Lời giải chi tiết:
Vì mặt cầu tâm I đi qua điểm A nên IA là bán kính của mặt cầu.
Bán kính của mặt cầu là: \(R = IA = \sqrt {{{\left( {0 - 1} \right)}^2} + {{\left( {4 - 2} \right)}^2} + {{\left( {5 - 3} \right)}^2}} = 3\).
Đường kính của mặt cầu là 2R = 2.3 = 6.
Các bài khác cùng chuyên mục













Danh sách bình luận