Giải mục 1 trang 60, 61 SGK Toán 12 tập 1 - Kết nối tri thức

Hệ trục tọa độ trong không gian

Tổng hợp đề thi giữa kì 1 lớp 12 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Lí - Hóa - Sinh

Lựa chọn câu để xem lời giải nhanh hơn

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 60 SGK Toán 12 Kết nối tri thức

Trong không gian, xét ba trục Ox, Oy, Oz có chung gốc O và đôi một vuông góc với nhau. Gọi \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) là các vectơ đơn vị trên các trục đó (H.2.35).

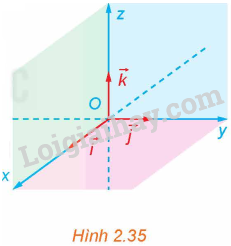
a) Gọi tên các mặt phẳng tọa độ có trong Hình 2.35.

b) Các mặt phẳng tọa độ trong Hình 2.35 có đôi một vuông góc với nhau không?

Phương pháp giải:

Sử dụng kiến thức về hai mặt phẳng vuông góc để chứng minh: Nếu mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia thì hai mặt phẳng đó vuông góc với nhau.

Lời giải chi tiết:

a) Các mặt phẳng có trong hình vẽ là: Mặt phẳng (Oxy), (Oyz), (Ozx).

b) Vì \(Ox \bot Oy,Oy \bot Oz\), Ox và Oz cắt nhau tại O và nằm trong mặt phẳng (Oxz) nên \(Oy \bot \left( {Oxz} \right)\). Mà \(Oy \subset \left( {Oxy} \right) \Rightarrow \left( {Oxz} \right) \bot \left( {Oxy} \right),Oy \subset \left( {Oyz} \right) \Rightarrow \left( {Oyz} \right) \bot \left( {Oxz} \right)\)

Chứng minh tương tự ta có: \(\left( {Oyz} \right) \bot \left( {Oxy} \right)\)

Vậy ba mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau.

Trả lời Câu hỏi trang 61 SGK Toán 12 Kết nối tri thức

Góc căn phòng trong Hình 2.34 có gợi lên hình ảnh về hệ tọa độ Oxyz trong không gian hay không? Nếu có hãy mô tả gốc tọa độ và các mặt phẳng tọa độ trong hình ảnh đó.

Phương pháp giải:

Sử dụng kiến thức hệ về hệ tọa độ trong không gian để mô tả: Trong không gian, ba trục Ox, Oy, Oz đôi một vuông góc với nhau tại gốc O của mỗi trục. Hệ ba trục tọa độ như vậy được gọi là hệ trục tọa độ Descartes vuông góc Oxyz (hay đơn giản là hệ tọa độ Oxyz). Điểm O được gọi là gốc tọa độ, các mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau và được gọi là các mặt phẳng tọa độ. Không gian với hệ tọa độ Oxyz còn được gọi là không gian Oxyz.

Lời giải chi tiết:

Góc căn phòng trong Hình 2.34 gợi lên hình ảnh về hệ trục tọa độ Oxyz trong không gian.

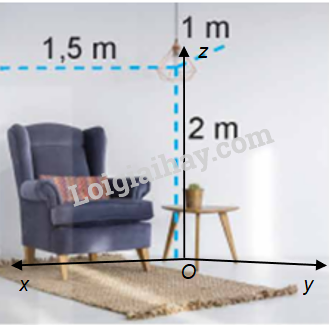
Mô tả: Hệ tọa độ Oxyz có:

+ Mặt phẳng (Oxy) là sàn nhà, hai mặt phẳng (Oyz), (Ozx) hai bức tường. Khi đó, ba mặt phẳng đôi một vuông góc với nhau.

+ Gốc tọa độ O (trùng với một góc phòng) là giao điểm của ba trục Ox, Oy, Oz.

LT1

Trả lời câu hỏi Luyện tập 1 trang 61 SGK Toán 12 Kết nối tri thức

Cho hình hộp chữ nhật ABCD.A’B’C’D’. Có thể lập một hệ tọa độ Oxyz có gốc O trùng với đỉnh C và các vectơ \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) lần lượt cùng hướng với các vectơ \(\overrightarrow {CB} ,\overrightarrow {CD} ,\overrightarrow {CC'} \) không? Vì sao?

Phương pháp giải:

Sử dụng kiến thức về hệ tọa độ trong không gian để mô tả: Trong không gian, ba trục Ox, Oy, Oz đôi một vuông góc với nhau tại gốc O của mỗi trục. Gọi \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) lần lượt là các vectơ đơn vị trên các trục Ox, Oy, Oz. Hệ ba trục tọa độ như vậy được gọi là hệ trục tọa độ Descartes vuông góc Oxyz (hay đơn giản là hệ tọa độ Oxyz). Điểm O được gọi là gốc tọa độ, các mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau và được gọi là các mặt phẳng tọa độ. Không gian với hệ tọa độ Oxyz còn được gọi là không gian Oxyz.

Lời giải chi tiết:

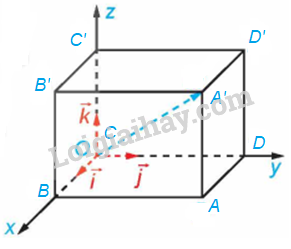
Vì ABCD. A’B’C’D’ là hình hộp chữ nhật nên các cạnh CC’, CB và CD đôi một vuông góc với nhau.

Các vectơ \(\overrightarrow {CB} ,\overrightarrow {CD} ,\overrightarrow {CC'} \) cùng có điểm đầu là C.

Do đó, suy ra có thể lập một hệ tọa độ Oxyz có gốc O trùng với đỉnh C và các vectơ \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) lần lượt cùng hướng với các vectơ \(\overrightarrow {CB} ,\overrightarrow {CD} ,\overrightarrow {CC'} \).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 2 trang 61, 62, 63 SGK Toán 12 tập 1 - Kết nối tri thức
Tọa độ của điểm, tọa độ của vectơ trong không gian
Giải bài tập 2.13 trang 64 SGK Toán 12 tập 1 - Kết nối tri thức
Trong không gian Oxyz, cho ba vectơ \(\overrightarrow a \), \(\overrightarrow b \), \(\overrightarrow c \) đều khác \(\overrightarrow 0 \) và có giá đôi một vuông góc. Những mệnh đề nào sau đây là đúng? a) Có thể lập được một hệ tọa độ Oxyz có các trục tọa độ lần lượt song song với giá của các vectơ \(\overrightarrow a \), \(\overrightarrow b \), \(\overrightarrow c \). b) Có thể lập được một hệ tọa độ Oxyz có các trục tọa độ lần lượt trùng với giá của các vectơ \(\overrightarrow a \), \(\over
Giải bài tập 2.14 trang 64 SGK Toán 12 tập 1 - Kết nối tri thức
Hãy mô tả hệ tọa độ Oxyz trong căn phòng ở Hình 2.44 sao cho gốc O trùng với góc trên của căn phòng, khung tranh nằm trong mặt phẳng (Oxy) và mặt trần nhà trùng với mặt phẳng (Oxz).
Giải bài tập 2.15 trang 65 SGK Toán 12 tập 1 - Kết nối tri thức
Trong không gian Oxyz, xác định tọa độ của vectơ \(\overrightarrow {AB} \) trong mỗi trường hợp sau: a) \(A\left( {0;0;0} \right)\) và \(B\left( {4;2; - 5} \right)\); b) \(A\left( {1; - 3;7} \right)\) và \(B\left( {1; - 3;7} \right)\); c) \(A\left( {5;4;9} \right)\) và \(B\left( { - 5;7;2} \right)\).
Giải bài tập 2.16 trang 65 SGK Toán 12 tập 1 - Kết nối tri thức
Trong không gian Oxyz, xác định tọa độ của điểm A trong mỗi trường hợp sau: a) A trùng với gốc tọa độ; b) A nằm trên tia Ox và \(OA = 2\); c) A nằm trên tia đối của tia Oy và \(OA = 3\).
Giải bài tập 2.17 trang 65 SGK Toán 12 tập 1 - Kết nối tri thức
Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc O và các đỉnh D, B, A’ có tọa độ lần lượt là (2; 0; 0), (0; 4; 0), (0; 0; 3) (H.2.45). Xác định tọa độ của các đỉnh còn lại của hình hộp chữ nhật.
Giải bài tập 2.19 trang 65 SGK Toán 12 tập 1 - Kết nối tri thức
Trong vận dụng 2, hãy giải thích vì sao tại mỗi thời điểm chiếc máy bay di chuyển trên đường băng thì tọa độ của nó luôn có dạng (x; y; 0) với x, y là hai số thực nào đó.
Giải bài tập 2.18 trang 65 SGK Toán 12 tập 1 - Kết nối tri thức
Trong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ có (Aleft( {1;1; - 1} right),Bleft( {0;3;0} right),C'left( {2; - 3;6} right)). a) Xác định tọa độ của điểm C. b) Xác định các tọa độ đỉnh còn lại của hình hộp.
Lý thuyết Hệ trục tọa độ trong không gian Toán 12 Kết nối tri thức
1. Hệ trục tọa độ trong không gian