-
Giải Toán 12 tập 1 - Cánh diều
-
Giải Toán 12 tập 2 - Cánh diều
Giải mục 1 trang 17, 19, 20 SGK Toán 12 tập 2 - Cánh diều
Định nghĩa tích phân
Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Cánh diều
Toán - Văn - Anh - Hoá - Sinh - Sử - Địa
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 17 SGK Toán 12 Cánh diều
Cho hàm số \(y = f(x) = {x^2}\) (Hình 4). Xét hình phẳng (được tô màu) gồm tất cả điểm M(x;y) trên mặt phẳng tọa độ sao cho \(1 \le x \le 2\) và \(0 \le y \le {x^2}\). Hình phẳng đó được gọi là hình thang cong AMNB giới hạn bởi đồ thị của hàm số \(f(x) = {x^2}\), trục Ox và hai đường thẳng x = 1 và x = 2.
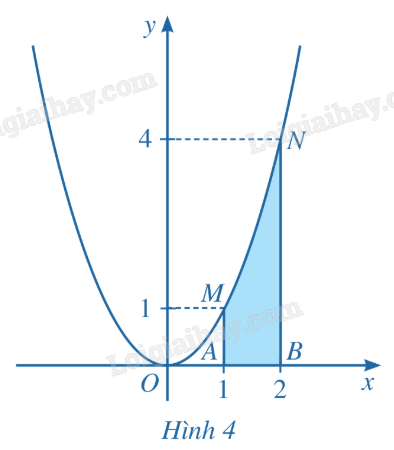
Chia đoạn [1;2] thành n phần bằng nhau bởi các điểm chia: \({x_0} = 1,{x_1} = 1 + \frac{1}{n},{x_2} = 1 + \frac{2}{n},...,{x_{n - 1}} = 1 + \frac{{n - 1}}{n},{x_n} = 1 + \frac{n}{n} = 2\) (Hình 5).
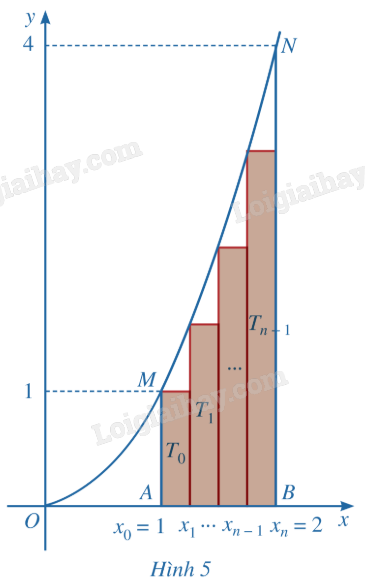
a) Tính diện tích \({T_0}\) của hình chữ nhật dựng trên đoạn \([{x_0};{x_1}]\) với chiều cao là \(f({x_0})\).
Tính diện tích \({T_1}\) của hình chữ nhật dựng trên đoạn \([{x_1};{x_2}]\) với chiều cao là \(f({x_1})\).
Tính diện tích \({T_2}\) của hình chữ nhật dựng trên đoạn \([{x_2};{x_3}]\) với chiều cao là \(f({x_2})\).
…
Tính diện tích \({T_{n - 1}}\) của hình chữ nhật dựng trên đoạn \([{x_{n - 1}};{x_n}]\) với chiều cao là \(f({x_{n - 1}})\).
b) Đặt \({S_n} = {T_0} + {T_1} + {T_2} + ... + {T_{n - 1}}\). Chứng minh rằng: \({S_n} = \frac{1}{n}[f({x_0}) + f({x_1}) + f({x_2}) + ... + f({x_{n - 1}})]\). Tổng \({S_n}\) gọi là tổng tích phân cấp n của hàm số \(f(x) = {x^2}\) trên đoạn [1;2].
Phương pháp giải:
a) Áp dụng công thức tính diện tích hình chữ nhật.
b) Biến đổi biểu thức cho thích hợp.
Lời giải chi tiết:
a) \({T_0} = f({x_0}).({x_1} - {x_0}) = f(1).({x_1} - 1)\);
\({T_1} = f({x_1}).({x_2} - {x_1})\);
\({T_2} = f({x_2}).({x_3} - {x_2})\);
…
\({T_{n - 1}} = f({x_{n - 1}}).({x_n} - {x_{n - 1}})\);
b) \({T_0} = f({x_0}).({x_1} - {x_0}) = f({x_0}).({x_0} + \frac{1}{n} - {x_0}) = \frac{{f({x_0})}}{n}\);
\({T_1} = f({x_1}).({x_2} - {x_1}) = f({x_1}).({x_1} + \frac{1}{n} - {x_1}) = \frac{{f({x_1})}}{n}\);
\({T_2} = f({x_2}).({x_3} - {x_2}) = f({x_2}).({x_2} + \frac{1}{n} - {x_2}) = \frac{{f({x_2})}}{n}\);
…
\({T_{n - 1}} = f({x_{n - 1}}).({x_n} - {x_{n - 1}})\)
\(= f({x_{n - 1}}).({x_{n - 1}} + \frac{1}{n} - {x_{n - 1}}) = \frac{{f({x_{n - 1}})}}{n}\).
Vậy \({S_n} = {T_0} + {T_1} + {T_2} + ... + {T_{n - 1}}\)
\(= \frac{1}{n}[f({x_0}) + f({x_1}) + f({x_2}) + ... + f({x_{n - 1}})]\).
LT1
Trả lời câu hỏi Luyện tập 1 trang 19 SGK Toán 12 Cánh diều
Cho đồ thị hàm số y = f(x) = 2x (\(x \in [0;2]\)). Xét tam giác vuông OAB giới hạn bởi đồ thị của hàm số f(x) = 2x, trục Ox và đường thẳng x = 2.
a) Tính diện tích tam giác vuông OAB.
b) Giả sử F(x) là một nguyên hàm của f(x) = 2x trên đoạn [0;2]. Tính F(2) – F(0). Từ đó hãy chứng tỏ rằng \({S_{OAB}} = F(2) - F(0)\).
Phương pháp giải:
a) Tìm tọa độ các điểm A, B. Từ đó tính diện tích tam giác OAB.
b) Áp dụng công thức nguyên hàm của hàm số lũy thừa.
Lời giải chi tiết:
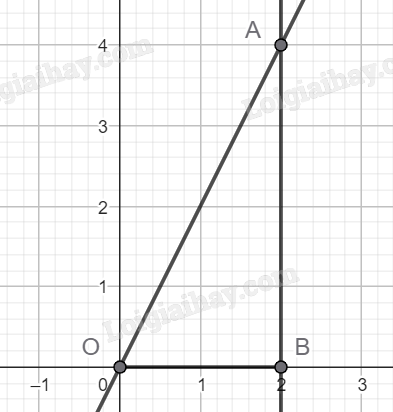
a) Ta có f(2) = 2.2 = 4. Do đó giao điểm của đồ thị f(x) = 2x và đường thẳng x = 2 có tọa độ (2;4).
Đường thẳng x = 2 cắt trục hoành tại điểm có hoành độ bằng 2.
Giả sử A(2;4) và B(2;0).
Ta có \({S_{OAB}} = \frac{1}{2}OB.AB = \frac{1}{2}2.4 = 4\).
b) Ta có \(F(x) = \int {f(x)dx} = \int {2xdx} = {x^2} + C\).
Xét \(F(2) - F(0) = {2^2} + C - ({0^2} + C) = 4\).
Vậy \(F(2) - F(0) = {S_{OAB}}\).
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 20 SGK Toán 12 Cánh diều
Cho hàm số \(f(x) = {x^2}\).
a) Chứng tỏ \(F(x) = \frac{{{x^3}}}{3}\), \(G(x) = \frac{{{x^3}}}{3} + C\) là các nguyên hàm của hàm số \(f(x) = {x^2}\).
b) Chứng minh rằng \(F(b) - F(a) = G(b) - G(a)\), tức là hiệu số \(F(b) - F(a)\) không phụ thuộc việc chọn nguyên hàm.
Phương pháp giải:
Cho hàm số f(x) xác định trên K. Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi x thuộc K.
Lời giải chi tiết:
a) \(F'(x) = G'(x) = {x^2} = f(x)\) nên \(F(x) = \frac{{{x^3}}}{3}\), \(G(x) = \frac{{{x^3}}}{3} + C\) là các nguyên hàm của hàm số \(f(x) = {x^2}\).
b) \(F(b) - F(a) = \frac{{{b^3}}}{3} - \frac{{{a^3}}}{3}\).
\(G(b) - G(a) = \frac{{{b^3}}}{3} + C - \frac{{{a^3}}}{3} - C = \frac{{{b^3}}}{3} - \frac{{{a^3}}}{3}\).
\( \Rightarrow F(b) - F(a) = G(b) - G(a)\).
LT2
Trả lời câu hỏi Luyện tập 2 trang 20 SGK Toán 12 Cánh diều
Tính \(\int\limits_0^\pi {\cos udu} \).
Phương pháp giải:
Áp dụng định nghĩa tích phân.
Lời giải chi tiết:
\(\int\limits_0^\pi {\cos udu} = \sin u\left| {\begin{array}{*{20}{c}}{^\pi }\\{_0}\end{array}} \right. = \sin \pi - \sin 0 = 0\).
Bình luận
Chia sẻ
- Giải mục 2 trang 21, 22 SGK Toán 12 tập 2 - Cánh diều
- Giải mục 3 trang 23, 24, 25 SGK Toán 12 tập 2 - Cánh diều
- Giải bài tập 1 trang 26 SGK Toán 12 tập 2 - Cánh diều
- Giải bài tập 2 trang 26 SGK Toán 12 tập 2 - Cánh diều
- Giải bài tập 3 trang 26 SGK Toán 12 tập 2 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Cánh diều - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
Các bài khác cùng chuyên mục
