Đề thi học kì 1 môn toán lớp 10 năm 2019 - 2020 trường THPT Đào Duy Từ

Mã đề thi 486

PHẦN I : TRẮC NGHIỆM

Câu 1 (TH): Nghiệm của hệ phương trình \(\left\{ \begin{array}{l}\sqrt 2 x - y =  - 1\\3x - \sqrt 2 y = 2\end{array} \right.\) là

A. \(\left\{ \begin{array}{l}x = 2 - \sqrt 2 \\y = 3 - 2\sqrt 2 \end{array} \right.\)   

B. \(\left\{ \begin{array}{l}x = \sqrt 2  - 2\\y = 2\sqrt 2  - 3\end{array} \right.\)   

C. \(\left\{ \begin{array}{l}x = 2 + \sqrt 2 \\y = 3 + 2\sqrt 2 \end{array} \right.\)   

D. \(\left\{ \begin{array}{l}x = \sqrt 2  + 2\\y = 2\sqrt 2  - 3\end{array} \right.\)

Câu 2 (TH): Cho \(\overrightarrow u  = \left( {2; - 2} \right),\,\,\overrightarrow v  = \left( {1;8} \right)\). Khẳng định nào sau đây là đúng ?

A. \(\overrightarrow u  + \overrightarrow v \) và \(\overrightarrow b  = \left( {1;2} \right)\) cùng hướng 

B.  \(2\overrightarrow u  + \overrightarrow v ,\,\,\overrightarrow v \) cùng phương              

C. \(\overrightarrow u ,\,\,\overrightarrow v \) cùng phương           

D. \(\overrightarrow u  - \overrightarrow v \) và \(\overrightarrow a  = \left( {1; - 10} \right)\) ngược hướng

Câu 3 (TH): Hàm số nào trong 4 phương án liệt kê ở A, B, C, D có đồ thị như hình bên ?

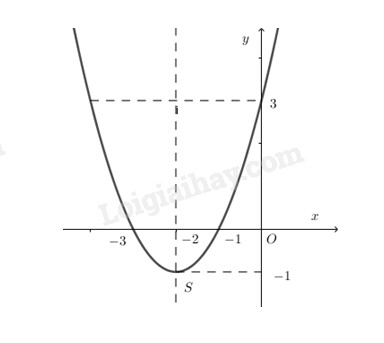
A. \(y = {x^2} - 4x + 3\)                                     B. \(y = 2{x^2} + 8x + 3\)                                     C. \(y = {x^2} + 4x + 3\)                                          D. \(y =  - {x^2} - 4x + 3\)

Câu 4 (NB): Trong các hàm số sau, hàm số bậc nhất là :

A. \(y = \dfrac{{2x - 2}}{3}\)                  B. \(y = \dfrac{{ - 2}}{{2x + 1}}\)         C. \(y = \dfrac{{mx + 1}}{x}\)           D. \(y = \sqrt {mx + x} \)

Câu 5 (TH): Điều kiện của \(m\) để phương trình \(\left( {{m^2} - 5} \right)x - 1 = m - x\) có nghiệm duy nhất là :

A. \(m \ne  \pm \sqrt 5 \)                   B. \(m \ne  - 2\)            C. \(m \ne 2\)        D. \(m \ne  \pm 2\)

Câu 6 (TH): Tam giác \(ABC\) vuông ở \(A\) và có góc \(\widehat B = 40^\circ \). Hệ thức nào sau đây là đúng ?

A. \(\left( {\overrightarrow {AB} ,\,\,\overrightarrow {BC} } \right) = 140^\circ \)    B. \(\left( {\overrightarrow {BC} ,\,\,\overrightarrow {AC} } \right) = 140^\circ \)         C. \(\left( {\overrightarrow {AC} ,\,\,\overrightarrow {CB} } \right) = 40^\circ \)     D. \(\left( {\overrightarrow {AB} ,\,\,\overrightarrow {CB} } \right) = 50^\circ \)

Câu 7 (TH): Cho \(3\) điểm \(A\left( {1;4} \right);\,\,B\left( {3;2} \right)\,;\,\,C\left( {5;4} \right)\). Chu vi tam giác \(ABC\) bằng bao nhiêu ?

A. \(8 + 8\sqrt 2 \)          B. \(4 + 4\sqrt 2 \)     C. \(4 + 2\sqrt 2 \)     D. \(2 + 2\sqrt 2 \)

Câu 8 (TH): Hệ phương trình \(\left\{ \begin{array}{l}\left( {m - 1} \right)x - y = 2\\ - 2x + my = 1\end{array} \right.\) có vô nghiệm khi?

A. \(\left[ \begin{array}{l}m =  - 1\\m = 2\end{array} \right.\)               B. \(\left[ \begin{array}{l}m = 1\\m =  - 2\end{array} \right.\)                              C. \(\left[ \begin{array}{l}m \ne  - 1\\m \ne 2\end{array} \right.\)                         D. \(\left[ \begin{array}{l}m =  - 1\\m =  - 2\end{array} \right.\)

Câu 9 (VD): Các đường thẳng \(y =  - 5\left( {x + 2} \right);y = ax + 3;y = 3x + a\) đồng quy với giá trị của \(a\) là:

A. \( - 11\)                     B. \( - 18\)                      C. \( - 12\)                                 D. \( - 10\)

Câu 10 (NB): Cho hàm số \(y = a{x^2} + bx + c\left( {a < 0} \right)\) có đồ thị \(\left( P \right)\). Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số đồng biến trên khoảng \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\)                  

B. Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\)       

C. Đồ thị luôn cắt trục hoành tại 2 điểm phân biệt.                                 

D. Đồ thị có trục đối xứng là đường thẳng \(x =  - \dfrac{b}{{2a}}\)

Câu 11 (VD): Số nghiệm của hệ phương trình \(\left\{ \begin{array}{l}{x^2} - {y^2} = 4\\xy = 5\end{array} \right.\) là:

A.\(3\)                            B. \(2\)                           C.\(1\)                            D. \(4\)

Câu 12 (TH): Gọi \({x_1},{x_2}\) là 2 nghiệm của phương trình \({x^2} - 3x + 2 = 0\). Tổng \(x_1^2 + x_2^2\) bằng:                                    

A. \(10\)                         B. \(9\)                           C. \(5\)                           D. \(8\)

Câu 13 (TH): Cho biết \(\sin \dfrac{\alpha }{3} = \dfrac{4}{5}\). Giá trị của \(P = 2{\sin ^2}\dfrac{\alpha }{3} + 5{\cos ^2}\dfrac{\alpha }{3}\) bằng bao nhiêu?

A.\(P = \dfrac{{93}}{{25}}\)            B.\(P = \dfrac{{109}}{{25}}\)      C.\(P = \dfrac{{111}}{{25}}\)       D. \(P = \dfrac{{107}}{{25}}\)

Câu 14 (VD): Cho tam giác \(ABC\) có \(A\left( { - 4;0} \right)\), \(B\left( {4;6} \right)\), \(C\left( { - 1;4} \right)\). Trực tâm của tam giác \(ABC\) có tọa độ là:

A. \(\left( {\dfrac{{76}}{7}; - \dfrac{{120}}{7}} \right)\)                 B. \(\left( {0;2} \right)\)                C.\(\left( {4;0} \right)\)        D. \(\left( { - \dfrac{{76}}{7};\dfrac{{120}}{7}} \right)\)

Câu 15 (VD): Hệ phương trình \(\left\{ \begin{array}{l}\dfrac{3}{x} + \dfrac{2}{y} = 12\\\dfrac{5}{x} - \dfrac{3}{y} = 1\end{array} \right.\) có nghiệm là:

A. \(\left( { - 1; - 2} \right)\)            B. \(\left( { - 1; - \dfrac{1}{2}} \right)\)       C. \(\left( {\dfrac{1}{2};\dfrac{1}{3}} \right)\)       D. \(\left( { - 1;2} \right)\)

Câu 16 (TH): Hệ phương trình \(\left\{ \begin{array}{l}mx + y = m - 3\\4x + my =  - 2\end{array} \right.\) có nghiệm duy nhất khi:

A. \(m = 2\)                   B. \(\left\{ \begin{array}{l}m \ne 2\\m \ne  - 2\end{array} \right.\)                                       C. \(m =  - 2\)                D. \(\left[ \begin{array}{l}m = 2\\m =  - 2\end{array} \right.\)

Câu 17 (TH): Điểm nào sau đây thuộc đồ thị hàm số \(y = \left| {2{x^2} - 3} \right|\)

A. \(\left( {0; - 3} \right)\)                                   B. \(\left( { - 1; - 1} \right)\)      C.\(\left( { - 2;5} \right)\)                  D.\(\left( { - 2;12} \right)\)               

Câu 18 (TH): Cho hàm số \(y = 2{x^2} - 4x + 3\) có đồ thị là Parabol \(\left( P \right)\). Mệnh đề nào sau đây sai?

A. \(\left( P \right)\) có trục đối xứng là \(d:x = 1\)                                  

B. \(\left( P \right)\) có đỉnh là \(S\left( { - 1;9} \right)\)                          

C. \(\left( P \right)\) không có giao điểm với trục hoành

D. \(\left( P \right)\) đi qua điểm \(M\left( { - 1;9} \right)\)

Câu 19 (VD): Cho tam giác \(ABC\) có \(A\left( {2;0} \right),\,\,B\left( {0;3} \right)\,,\,\,C\left( { - 3;1} \right)\). Đường thẳng \(d\) đi qua \(A\) và song song với \(BC\) có phương trình là

A. \(2x - 3y - 4 = 0\)       B. \(5x + y - 3 = 0\)   C. \(x + 5y - 15 = 0\) D. \(x - 15y + 15 = 0\)

Câu 20 (TH): Hàm số nào sau đây đồng biến trong khoảng \(\left( { - \infty ;0} \right)\) ?

A. \(y = \sqrt 2 {\left( {x + 1} \right)^2}\)       B. \(\sqrt 2 {x^2} + 1\)       C. \( - \sqrt 2 {\left( {x + 1} \right)^2}\)        D. \( - \sqrt 2 {x^2} + 1\)

Câu 21 (TH): Vectơ  nào dưới đây là một vectơ pháp tuyến của \(d:\left\{ \begin{array}{l}x =  - 1 + 2t\\y = 3 + t\end{array} \right.\)

A. \(\overrightarrow {{n_1}}  = \left( {2; - 1} \right)\)                    B. \(\overrightarrow {{n_3}}  = \left( {1; - 2} \right)\)                     C. \(\overrightarrow {{n_2}}  = \left( {1;2} \right)\)                          D. \(\overrightarrow {{n_4}}  = \left( {1;2} \right)\)

Câu 22 (VD): Cho phương trình \(\left( {1 - \sqrt 2 } \right){x^4} - \left( {\sqrt 2  - \sqrt 3 } \right){x^2} + \sqrt 3  = 0\). Số các nghiệm dương của phương trình là

A. \(2\)                           B. \(3\)                       C. \(4\)                      D. \(1\)

Câu 23 (VD): Trong hệ tọa độ \(Oxy\), cho ba điểm \(A\left( {1;1} \right)\,,\,\,B\left( {2; - 1} \right)\,,\,\,C\left( {4;3} \right)\). Tọa độ điểm \(D\) để \(ABDC\) là hình bình hành là :

A. \(D\left( {1;3} \right)\)                                B. \(D\left( {3;5} \right)\)               C. \(D\left( {3;1} \right)\)                          D. \(D\left( {5;1} \right)\)

Câu 24 (TH): Tam giác \(ABC\) có \(AB = 8cm,\,\,AC = 20cm\) và có diện tích bằng \(64c{m^2}\). Giá trị \(\sin A\) bằng

A. \(\sin A = \dfrac{{\sqrt 3 }}{2}\)                B. \(\sin A = \dfrac{8}{9}\)            C. \(\sin A = \dfrac{4}{5}\)                D. \(\sin A = \dfrac{3}{8}\)

Câu 25 (TH): Bảng biến thiên của hàm số \(y = 2{x^2} - 4x + 5\) là bảng nào sau đây ?

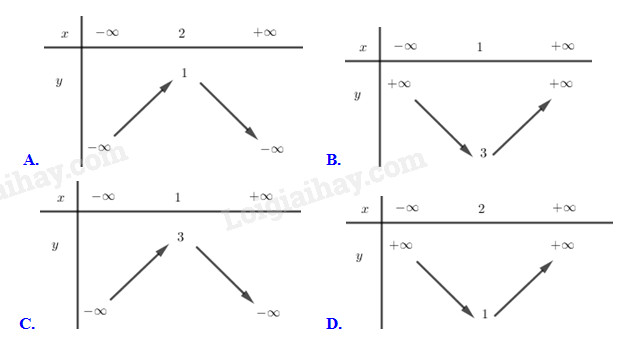
PHẦN 2 : TỰ LUẬN

Câu 1 (2 điểm): Giải các phương trình, hệ phương trình sau:

\(a)\,\,\left| {1 - 2x} \right| - \left| {x + 1} \right| = 7\)                       \(b)\,\,{x^4} + 2{x^2} - 3 = 0\)                                  \(c)\,\,\left\{ \begin{array}{l}{x^2} = 3x + 2y\\{y^2} = 3y + 2x\end{array} \right.\)

Câu 2 (1 điểm): Xác định hàm số bậc hai \(y = a{x^2} + bx + 3\) biết đồ thị hàm số của nó đi qua điểm \(A\left( { - 1;9} \right)\) và có trục đối xứng \(x =  - 2\).

Câu 3 (2 điểm): a) Cho tam giác \(ABC\) có \(A\left( {4;2} \right),\,\,B\left( { - 3; - 4} \right),\,\,C\left( {4; - 5} \right)\). Viết phương trình tổng quát của đường thẳng đi qua điểm \(A\) và song song với đường thẳng \(BC\).

b) Cho tam giác \(MNP\) có \(MN = 6,\,\,NP = 7\) và \(\widehat M = 60^\circ \). Tính góc \(\widehat N\) và \(\widehat P\).

ĐÁP ÁN

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn Loigiaihay.com

Câu 1 (TH):

Phương pháp:

Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số

Cách giải:

Ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}\sqrt 2 x - y =  - 1\\3x - \sqrt 2 y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - \sqrt 2 y =  - \sqrt 2 \\3x - \sqrt 2 y = 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 2 + \sqrt 2 \\\sqrt 2 x - y =  - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2 + \sqrt 2 \\y = \sqrt 2 \left( {2 + \sqrt 2 } \right) + 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 2 + \sqrt 2 \\y = 2\sqrt 2  + 3\end{array} \right.\end{array}\)

Vậy nghiệm của hệ phương trình là: \(\left( {x;y} \right) = \left( {2 + \sqrt 2 ;2\sqrt 2  + 3} \right)\)

Chọn C

Câu 2 (TH):

Phương pháp:

Cho véc tơ \(\overrightarrow u  = \left( {a;b} \right)\), khi đó \(\overrightarrow v  = k\overrightarrow u \,\left( {k \ne 0} \right)\) cùng hướng với \(\overrightarrow u  \Leftrightarrow k > 0\) và ngược hướng với \(\overrightarrow u  \Leftrightarrow k < 0.\)

Cách giải:

Ta có: \(\overrightarrow u  + \overrightarrow v  = \left( {2 + 1; - 2 + 8} \right) = \left( {3;6} \right) = 3\left( {1;2} \right) = 3\overrightarrow u \)

Nên \(\overrightarrow u  + \overrightarrow v \) và \(\overrightarrow u \)  cùng hướng, do đó A đúng.

Chọn A

Câu 3 (TH):

Phương pháp:

Xác định một số điểm thuộc đồ thị hàm số rồi thay tọa độ điểm vào các hàm số ở mỗi đáp án để chọn đáp án đúng.

Cách giải:

Từ hình vẽ ta thấy parabol quay bề lõm lên trên do đó \(a > 0\), loại D.

Các điểm \(\left( { - 2; - 1} \right);\left( { - 3;0} \right)\) thuộc đồ thị hàm số

Thay \(x =  - 2;y =  - 1\) vào hàm số ở A, B, C ta thấy chỉ có hàm số \(y = {x^2} + 4x + 3\) thỏa mãn nên C đúng.

Chọn C

Câu 4 (NB):

Phương pháp:

Hàm số bậc nhất có dạng \(y = ax + b\,\,\left( {a \ne 0} \right)\)

Cách giải:

Ta có \(y = \dfrac{{2x - 2}}{3} = \dfrac{2}{3}x - \dfrac{2}{3}\)  là hàm số bậc nhất nên A đúng.

Chọn A

Câu 5 (TH):

Phương pháp:

Phương trình \(ax + b = 0\) có nghiệm duy nhất khi \(a \ne 0.\)

Cách giải:

Ta có \(\left( {{m^2} - 5} \right)x - 1 = m - x \Leftrightarrow \left( {{m^2} - 4} \right)x - 1 - m = 0\)

Phương trình trên có nghiệm duy nhất \( \Leftrightarrow {m^2} - 4 \ne 0 \Leftrightarrow {m^2} \ne 4 \Leftrightarrow m \ne  \pm 2\)

Chọn D

Câu 6 (TH):

Phương pháp:

Để xác định góc giữa hai véc tơ ta đưa hai véc tơ đó về chung gốc.

Cách giải: 

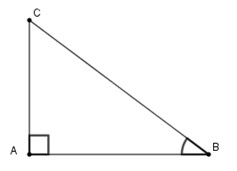
Ta có: \(\left( {\overrightarrow {AB} ;\overrightarrow {BC} } \right) = {180^0} - \left( {\overrightarrow {BA} ;\overrightarrow {BC} } \right) = {180^0} - \widehat B = {140^0}\)

Chọn A

Câu 7 (TH):

Phương pháp:

Chu vi tam giác bằng tổng ba cạnh.

Cho \(A\left( {{x_1};{y_1}} \right);\,B\left( {{x_2};{y_2}} \right) \Rightarrow AB = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \)

Cách giải:

Ta có:

\(\begin{array}{l}AB = \sqrt {{{\left( {3 - 1} \right)}^2} + {{\left( {2 - 4} \right)}^2}}  = 2\sqrt 2 \\AC = \sqrt {{{\left( {5 - 1} \right)}^2} + {{\left( {4 - 4} \right)}^2}}  = 4\\BC = \sqrt {{{\left( {5 - 3} \right)}^2} + {{\left( {4 - 2} \right)}^2}}  = 2\sqrt 2 \end{array}\)

Chu vi tam giác \(ABC\) bằng \(AB + BC + AC = 4 + 4\sqrt 2 .\)

Chọn B

Câu 8 (TH):

Phương pháp:

Thế \(y\) ở phương trình thứ nhất xuống phương trình thứ hai, rồi biện luận phương trình ẩn \(y\) tìm được.

Cách giải:

Ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}\left( {m - 1} \right)x - y = 2\\ - 2x + my = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = \left( {m - 1} \right)x - 2\\ - 2x + m\left( {\left( {m - 1} \right)x - 2} \right) = 1\,\left( * \right)\end{array} \right.\\\left( * \right) \Leftrightarrow  - 2x + \left( {{m^2} - m} \right)x - 2m = 1\\ \Leftrightarrow \left( {{m^2} - m - 2} \right)x = 1 + 2m\,\left( 1 \right)\end{array}\)

Để hệ phương trình vô nghiệm thì phương trình 1 vô nghiệm, nên:

\(\left\{ \begin{array}{l}{m^2} - m - 2 = 0\\1 + 2m \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m =  - 1\\m = 2\end{array} \right.\\m \ne  - \dfrac{1}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m =  - 1\\m = 2\end{array} \right.\)

Chọn A

Câu 9 (VD):

Phương pháp:

Tìm giao điểm của hai đường thẳng rồi thay tọa độ giao điểm đó vào phương trình đường thẳng còn lại.

Cách giải:

Xét các đường thẳng: \(\left( {{d_1}} \right):y =  - 5\left( {x + 2} \right);\left( {{d_2}} \right):y = ax + 3;\left( {{d_3}} \right):y = 3x + a\)

Để ba đường thẳng trên cắt nhau thì \(a \ne \left\{ { - 5;3} \right\}\)

Xét phương trình hoành độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_3}} \right)\) ta được:

\(\begin{array}{l} - 5\left( {x + 2} \right) = 3x + a \Leftrightarrow  - 5x - 10 = 3x + a\\ \Leftrightarrow 8x =  - a - 10 \Rightarrow x = \dfrac{{ - a - 10}}{8} \Rightarrow y = 3.\dfrac{{ - a - 10}}{8} + a = \dfrac{{5a - 30}}{8}\end{array}\)

Thay \(x = \dfrac{{ - a - 10}}{8};y = \dfrac{{5a - 30}}{8}\)  vào phương trình đường thẳng \(\left( {{d_2}} \right)\) ta được:

\(\begin{array}{l}\dfrac{{5a - 30}}{8} = a.\dfrac{{ - a - 10}}{8} + 3\\ \Leftrightarrow 5a - 30 =  - {a^2} - 10a + 24\\ \Leftrightarrow {a^2} + 15a - 54 = 0\\ \Leftrightarrow \left[ \begin{array}{l}a =  - 18\left( {tm} \right)\\a = 3\left( {ktm} \right)\end{array} \right.\end{array}\)

Vậy \(a =  - 18.\)

Chọn B

Câu 10 (NB):

Phương pháp:

Dựa vào tính chất hàm số và đồ thị hàm số \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)

Cách giải:

Hàm số \(y = a{x^2} + bx + c\left( {a < 0} \right)\) đồng biến trên khoảng \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\) và nghịch biến trên khoảng \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\)

Nên A, B sai.

Ta chưa kết luận được gì về số giao điểm của đồ thị hàm số đã cho với trục hoành.

Đồ thị hàm số \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\) có trục đối xứng là đường thẳng \(x =  - \dfrac{b}{{2a}}\) nên D đúng.

Chọn D.

Câu 11 (VD):

Phương pháp:

Giải hệ phương trình bằng phương pháp thế.

Cách giải:

Ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}{x^2} - {y^2} = 4\\xy = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = \dfrac{5}{x}\\{x^2} - {\left( {\dfrac{5}{x}} \right)^2} = 4\left( * \right)\end{array} \right.\\\left( * \right) \Leftrightarrow {x^2} - \dfrac{{25}}{{{x^2}}} = 4\\ \Rightarrow {x^4} - 25 = 4{x^2}\\ \Leftrightarrow {x^4} - 4{x^2} - 25 = 0\end{array}\)

Đặt \({x^2} = t \ge 0,\) ta có phương trình: \({t^2} - 4t - 25 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 2 + \sqrt {29} \left( {tm} \right)\\t = 2 - \sqrt {29} \left( {ktm} \right)\end{array} \right.\)

Suy ra \({x^2} = 2 + \sqrt {29}  \Leftrightarrow \left[ \begin{array}{l}x = \sqrt {2 + \sqrt {29} }  \Rightarrow y = \dfrac{5}{{\sqrt {2 + \sqrt {29} } }}\\x =  - \sqrt {2 + \sqrt {29} }  \Rightarrow y =  - \dfrac{5}{{\sqrt {2 + \sqrt {29} } }}\end{array} \right.\)

Vậy hệ phương trình có hai nghiệm.

Chọn B.

Câu 12 (TH):

Phương pháp:

Hệ thức Vi-ét:

Nếu \({x_1};{x_2}\) là hai nghiệm của phương trình \(a{x^2} + bx + c = 0\) thì ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - \dfrac{b}{a}\\{x_1}.{x_2} = \dfrac{c}{a}\end{array} \right.\)

Cách giải:

Xét phương trình \({x^2} - 3x + 2 = 0\) có \(\Delta  = 1 > 0\) nên có hai nghiệm phân biệt \({x_1};{x_2}.\)

Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 3\\{x_1}{x_2} = 2\end{array} \right.\)

Nên \(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {3^2} - 2.2 = 5\)

Chọn C.

Câu 13 (TH):

Phương pháp:

Sử dụng hệ thức \({\sin ^2}a + {\cos ^2}a = 1\,\)

Cách giải:

Ta có \({\sin ^2}\dfrac{\alpha }{3} + {\cos ^2}\dfrac{\alpha }{3} = 1 \Rightarrow {\cos ^2}\dfrac{\alpha }{3} = 1 - {\left( {\dfrac{4}{5}} \right)^2} = \dfrac{9}{{25}}\)

Khi đó: \(P = 3{\sin ^2}\dfrac{\alpha }{3} + 5{\cos ^2}\dfrac{\alpha }{3} = 3.{\left( {\dfrac{4}{5}} \right)^2} + 5.\dfrac{9}{{25}} = \dfrac{{93}}{{25}}\)

Chọn A

Câu 14 (VD):

Phương pháp:

Gọi \(H\left( {x;y} \right)\) là trực tâm tam giác \(ABC\). Sau đó giải hệ phương trình: \(\left\{ \begin{array}{l}\overrightarrow {AH} .\overrightarrow {BC}  = 0\\\overrightarrow {BH} .\overrightarrow {AC}  = 0\end{array} \right.\)  để tìm \(x;y \Rightarrow H\)

Cách giải:

Ta có: \(\overrightarrow {BC}  = \left( { - 5; - 2} \right);\,\overrightarrow {AC}  = \left( {3;4} \right)\)

Gọi \(H\left( {x;y} \right)\) là trực tâm tam giác \(ABC\). Suy ra \(\overrightarrow {AH}  = \left( {x + 4;y} \right);\,\overrightarrow {BH}  = \left( {x - 4;y - 6} \right)\)

Khi đó: \(AH \bot BC;\,BH \bot AC\) nên \(\left\{ \begin{array}{l}\overrightarrow {AH} .\overrightarrow {BC}  = 0\\\overrightarrow {BH} .\overrightarrow {AC}  = 0\end{array} \right.\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\left( {x + 4} \right).\left( { - 5} \right) - 2y = 0\\\left( {x - 4} \right).3 + \left( {y - 6} \right).4 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}5x + 2y + 20 = 0\\3x + 4y - 36 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{76}}{7}\\y =  - \dfrac{{120}}{7}\end{array} \right.\end{array}\)

Suy ra \(H\left( {\dfrac{{76}}{7}; - \dfrac{{120}}{7}} \right)\)

Chọn A.

Câu 15 (VD):

Phương pháp:

Giải hệ phương trình bằng phương pháp cộng đại số

Cách giải:

Ta có:

 \(\begin{array}{l}DK:\,x \ne 0;y \ne 0\\\left\{ \begin{array}{l}\dfrac{3}{x} + \dfrac{2}{y} = 12\\\dfrac{5}{x} - \dfrac{3}{y} = 1\end{array} \right.\,\,\\ \Leftrightarrow \left\{ \begin{array}{l}\dfrac{9}{x} + \dfrac{6}{y} = 36\\\dfrac{{10}}{x} - \dfrac{6}{y} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{3}{x} + \dfrac{2}{y} = 12\\\dfrac{{19}}{x} = 38\end{array} \right.\,\\ \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{2}\\\dfrac{2}{y} = 6\end{array} \right. \Leftrightarrow \,\,\left\{ \begin{array}{l}x = \dfrac{1}{2}\\y = \dfrac{1}{3}\end{array} \right.\left( {tm} \right)\end{array}\)

Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {\dfrac{1}{2};\dfrac{1}{3}} \right)\)

Chọn C

Câu 16 (TH):

Phương pháp:

Rút \(y\) ở phương trình thứ nhất thế vào phương trình thứ hai rồi biện luận theo phương trình ẩn \(x\) thu được.

Cách giải:

Ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}mx + y = m - 3\\4x + my =  - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = m - 3 - mx\\4x + m\left( {m - 3 - mx} \right) =  - 2\left( * \right)\end{array} \right.\\\left( * \right) \Rightarrow 4x - {m^2}x + {m^2} - 3m =  - 2\\ \Leftrightarrow \left( {{m^2} - 4} \right)x = {m^2} - 3m + 2\end{array}\)

Hệ phương trình có nghiệm duy nhất khi \({m^2} - 4 \ne 0 \Leftrightarrow m \ne  \pm 2.\)

Chọn B

Câu 17 (TH):

Phương pháp:

Thay tọa độ các điểm ở đáp án vào hàm số để chọn.

Điểm \(M\left( {{x_0};{y_0}} \right)\) thuộc đồ thị hàm số \(y = f\left( x \right) \Leftrightarrow {y_0} = f\left( {{x_0}} \right)\)

Cách giải:

Thay tọa độ điểm \(C\left( { - 2;5} \right)\) vào hàm số ta được: \(5 = \left| {2.{{\left( { - 2} \right)}^2} - 3} \right| \Leftrightarrow 5 = 5\left( {ld} \right)\)  nên điểm \(C\left( { - 2;5} \right)\) thuộc đồ thị hàm số đã cho.

Chọn C

Câu 18 (TH):

Phương pháp:

Đồ thị hàm số \(y = a{x^2} + bx + c\,\left( {a \ne 0} \right)\)có trục đối xứng \(x =  - \dfrac{b}{{2a}}\), có đỉnh là điểm \(I\left( { - \dfrac{b}{{2a}}; - \dfrac{\Delta }{{4a}}} \right)\)

Cách giải:

Đồ thị hàm số \(y = 2{x^2} - 4x + 3\) có trục đối xứng \(x = 1,\) có đỉnh là \(I\left( {1;1} \right)\) nên A đúng, B sai.

Phương trình \(2{x^2} - 4x + 3 = 0\) vô nghiệm do có \(\Delta  =  - 4 < 0\) nên đồ thị hàm số \(y = 2{x^2} - 4x + 3\) không có giao điểm với trục hoành. Do đó, C đúng.

Thay \(x =  - 1\) vào hàm số ta được \(y = 2.{\left( { - 1} \right)^2} - 4.\left( { - 1} \right) + 3 = 9\) nên điểm \(M\left( { - 1;9} \right)\) thuộc đồ thị hàm số \(y = 2{x^2} - 4x + 3.\) Do đó, D đúng.

Chọn B.

Câu 19 (VD):

Phương pháp:

Đường thẳng đi qua \(M\left( {{x_0};{y_0}} \right)\) và có VTPT \(\overrightarrow n  = \left( {a;b} \right)\) có phương trình tổng quát là:

\(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\)

Cách giải:

\(\overrightarrow {BC}  = \left( { - 3; - 2} \right)\) là 1 VTCP của đường thẳng \(d\)

Suy ra 1 VTPT của đường thẳng \(d\) là: \(\overrightarrow n \left( {2; - 3} \right)\)

Phương trình tổng quát của đường thẳng \(d:2\left( {x - 2} \right) - 3y = 0 \Leftrightarrow 2x - 3y - 4 = 0\)

Chọn A

Câu 20 (TH):

Phương pháp:

Hàm số \(y = a{x^2} + bx + c\,\left( {a < 0} \right)\) đồng biến trên khoảng \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\)

Hàm số \(y = a{x^2} + bx + c\,\left( {a > 0} \right)\) đồng biến trên khoảng \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\)

Cách giải:

Từ yêu cầu đề bài ta suy ra hàm số cần tìm có hệ số \(a < 0\) nên loại A và B.

Hàm số \(y =  - \sqrt 2 {\left( {x + 1} \right)^2} =  - \sqrt 2 {x^2} - 2\sqrt 2 x - \sqrt 2 \) đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\) nên C sai.

Hàm số \(y =  - \sqrt 2 {x^2} + 1\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) nên D đúng.

Chọn D.

Câu 21 (TH):

Phương pháp:

Phương trình đường thẳng \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\)  có 1 VTCP là \(\overrightarrow u  = \left( {a;b} \right)\) và có 1 VTPT là \(\overrightarrow n  = \left( {b; - a} \right)\)

Cách giải:

1 VTCP của đường thẳng là \(\overrightarrow u  = \left( {2;1} \right)\) suy ra 1 VTPT là \(\overrightarrow n  = \left( {1; - 2} \right)\).

Chọn B.

Câu 22 (VD):

Phương pháp:

Đặt \({x^2} = t \ge 0\) rồi đưa về phương trình bậc hai. Từ đó tìm được số nghiệm của phương trình đã cho.

Cách giải:

Đặt \({x^2} = t \ge 0\) ta được phương trình:

\(\left( {1 - \sqrt 2 } \right){t^2} - \left( {\sqrt 2  - \sqrt 3 } \right)t + \sqrt 3  = 0\)

Phương trình trên có \(ac = \left( {1 - \sqrt 2 } \right).\sqrt 3  < 0\) nên có hai nghiệm trái dấu \({t_1} < 0\left( L \right);{t_2} > 0\left( N \right)\)

Thay lại cách đặt ta được \({x^2} = {t_2} \Rightarrow x =  \pm \sqrt {{t_2}} \)  hay phương trình đã cho có 2 nghiệm phân biệt.

Chọn A

Câu 23 (VD):

Phương pháp:

\(ABDC\) là hình bình hành khi \(\overrightarrow {AB}  = \overrightarrow {CD} \)

Hai véc tơ bằng nhau khi hoành độ bằng nhau và tung độ bằng nhau.

Cách giải:

Gọi \(D\left( {x;y} \right) \Rightarrow \overrightarrow {CD}  = \left( {x - 4;y - 3} \right)\); \(\overrightarrow {AB}  = \left( {1; - 2} \right)\)

Để \(ABDC\) là hình bình hành thì \(\overrightarrow {AB}  = \overrightarrow {CD} \)

\( \Leftrightarrow \left\{ \begin{array}{l}x - 4 = 1\\y - 3 =  - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 1\end{array} \right.\)  nên \(D\left( {5;1} \right)\)

Chọn D

Câu 24 (TH):

Phương pháp:

Sử dụng công thức diện tích \({S_{ABC}} = \dfrac{1}{2}AB.AC\sin A\)

Cách giải:

Ta có: \({S_{ABC}} = \dfrac{1}{2}AB.AC\sin A\) nên \(\sin A = \dfrac{{2{S_{ABC}}}}{{AB.AC}} = \dfrac{{2.64}}{{8.20}} = \dfrac{4}{5}.\)

Chọn C.

Câu 25 (TH):

Phương pháp:

Hàm số \(y = a{x^2} + bx + c\) với \(a > 0\) nghịch biến trên \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\) và đồng biến trên \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\)

Cách giải:

Trục đối xứng \(x =  - \dfrac{b}{{2a}} = 1\)

Đỉnh parabol \(I\left( {1;3} \right)\)

Vì \(a = 2 > 0\) nên hàm số nghịch biến trên \(\left( { - \infty ;1} \right)\) và đồng biến trên \(\left( {1; + \infty } \right)\)

Ta có BBT:

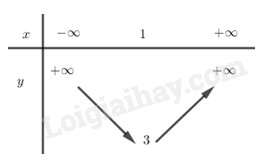
Chọn B.

PHẦN II: TỰ LUẬN

Câu 1:

Phương pháp:

a) Phá dấu giá trị tuyệt đối và giải phương trình thu được.

b) Đặt \(t = {x^2}\) và giải phương trình.

c) Trừ vế với vế các phương trình đưa về dạng tích.

Cách giải:

a) \(\left| {1 - 2x} \right| - \left| {x + 1} \right| = 7\) \( \Leftrightarrow \left| {2x - 1} \right| - \left| {x + 1} \right| = 7\)

+) Nếu \(x \ge \dfrac{1}{2}\) thì:

\(\begin{array}{l}\left| {2x - 1} \right| - \left| {x + 1} \right| = 7\\ \Leftrightarrow \left( {2x - 1} \right) - \left( {x + 1} \right) = 7\\ \Leftrightarrow 2x - 1 - x - 1 = 7\\ \Leftrightarrow x - 2 = 7\\ \Leftrightarrow x = 9\left( {TM} \right)\end{array}\)

+) Nếu \( - 1 < x < \dfrac{1}{2}\) thì:

\(\begin{array}{l}\left| {2x - 1} \right| - \left| {x + 1} \right| = 7\\ \Leftrightarrow \left( { - 2x + 1} \right) - \left( {x + 1} \right) = 7\\ \Leftrightarrow  - 2x + 1 - x - 1 = 7\\ \Leftrightarrow  - 3x = 7 \Leftrightarrow x =  - \dfrac{7}{3}\left( {KTM} \right)\end{array}\)

+) Nếu \(x \le  - 1\) thì:

\(\begin{array}{l}\left| {2x - 1} \right| - \left| {x + 1} \right| = 7\\ \Leftrightarrow \left( { - 2x + 1} \right) - \left( { - x - 1} \right) = 7\\ \Leftrightarrow  - 2x + 1 + x + 1 = 7\\ \Leftrightarrow  - x + 2 = 7 \Leftrightarrow x =  - 5\left( {TM} \right)\end{array}\)

Vậy phương trình có tập nghiệm \(S = \left\{ {9; - 5} \right\}\)

b) \({x^4} + 2{x^2} - 3 = 0\)

Đặt \(t = {x^2} \ge 0\) ta được:

\({t^2} + 2t - 3 = 0 \Leftrightarrow \left( {t - 1} \right)\left( {t + 3} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}t - 1 = 0\\t + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = 1\left( {TM} \right)\\t =  - 3\left( {KTM} \right)\end{array} \right.\)

Suy ra \({x^2} = 1 \Leftrightarrow x =  \pm 1\).

Vậy phương trình có tập nghiệm \(S = \left\{ { \pm 1} \right\}\).

c) \(\left\{ \begin{array}{l}{x^2} = 3x + 2y\,\,\left( 1 \right)\\{y^2} = 3y + 2x\end{array} \right.\)

Trừ hai phương trình vế với vế ta được:

\({x^2} - {y^2} = x - y\) \( \Leftrightarrow \left( {x - y} \right)\left( {x + y} \right) - \left( {x - y} \right) = 0\) \( \Leftrightarrow \left( {x - y} \right)\left( {x + y - 1} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x - y = 0\\x + y - 1 = 0\end{array} \right.\) 

+) Nếu \(x - y = 0 \Leftrightarrow y = x\) thay vào \(\left( 1 \right)\) ta được:

\({x^2} = 3x + 2x \Leftrightarrow {x^2} - 5x = 0\) \( \Leftrightarrow x\left( {x - 5} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 0\\x = 5 \Rightarrow y = 5\end{array} \right.\)

+) Nếu \(x + y - 1 = 0 \Leftrightarrow y = 1 - x\) thay vào \(\left( 1 \right)\) ta được:

\({x^2} = 3x + 2\left( {1 - x} \right)\) \( \Leftrightarrow {x^2} = x + 2\) \( \Leftrightarrow {x^2} - x - 2 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x =  - 1 \Rightarrow y = 2\\x = 2 \Rightarrow y =  - 1\end{array} \right.\)

Vậy hệ có nghiệm \(\left( {x,y} \right) \in \left\{ {\left( {0;0} \right),\left( {5;5} \right),\left( { - 1;2} \right),\left( {2; - 1} \right)} \right\}\).

Câu 2:

Phương pháp:

Sử dụng lý thuyết hàm số bậc hai:

- Trục đối xứng \(x =  - \dfrac{b}{{2a}}\).

- Điểm \(M \in \left( P \right)\) thì tọa độ của \(M\) thỏa mãn công thức hàm số của \(\left( P \right)\).

Cách giải:

- Trục đối xứng \(x =  - 2\) nên \( - \dfrac{b}{{2a}} =  - 2 \Leftrightarrow b = 4a\) (1)

- Đồ thị đi qua \(A\left( { - 1;9} \right)\) nên \(9 = a.{\left( { - 1} \right)^2} + b.\left( { - 1} \right) + 3\) \( \Leftrightarrow a - b = 6\) (2)

Thay (1) vào (2) ta có: \(a - 4a = 6 \Leftrightarrow  - 3a = 6 \Leftrightarrow a =  - 2\).

Suy ra \(b = 4.\left( { - 2} \right) =  - 8\).

Vậy hàm số \(y =  - 2{x^2} - 8x + 3\).

Câu 3:

Phương pháp:

a) Phương trình đường thẳng đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) và nhận \(\overrightarrow n  = \left( {a;b} \right)\) làm VTPT là \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\).

b) Sử dụng hệ thức lượng trong tam giác.

Cách giải:

a) Ta có: \(\overrightarrow {BC}  = \left( {7; - 1} \right)\).

Đường thẳng qua \(A\left( {4;2} \right)\) và song song \(BC\) nên nhận \(\overrightarrow n  = \left( {1;7} \right)\) làm VTPT.

Vậy \(1\left( {x - 4} \right) + 7\left( {y - 2} \right) = 0\) \( \Leftrightarrow x + 7y - 18 = 0\).

b) Áp dụng định lí sin trong tam giác \(MNP\) ta có:

\(\dfrac{{NP}}{{\sin \widehat M}} = \dfrac{{MN}}{{\sin \widehat P}}\) \( \Rightarrow \dfrac{7}{{\sin {{60}^0}}} = \dfrac{6}{{\sin \widehat P}}\) \( \Leftrightarrow \sin \widehat P = \dfrac{{6.\sin {{60}^0}}}{7} = \dfrac{{3\sqrt 3 }}{7}\) \( \Rightarrow \widehat P \approx {48^0}\).

Lại có \(\widehat M + \widehat N + \widehat P = {180^0}\) nên \(\widehat N = {180^0} - \widehat M - \widehat P\) \( \approx {180^0} - {60^0} - {48^0} = {72^0}\).

Vậy \(\widehat P \approx {48^0},\widehat N \approx {72^0}\).

Loigiaihay.com