Đề thi học kì 1 môn toán lớp 10 năm 2019 - 2020 sở GDĐT Hà Nam

Câu 1: Trong các phương trình dưới đây, phương trình nào tương đương với phương trình \({x^2} = 4?\)  

A. \(\left| x \right| = 2\)                          

B. \({x^2} - 2x + 4 = 0\)                        

C. \({x^2} + \sqrt x  = \sqrt x  + 4\)                            

D. \({x^2} - 2x - 4 = 0\)

Câu 2: Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD với A(2;– 2), B(3; 4), C(– 1; 5). Khi đó điểm D có tọa độ là:

A. (0; 11)                   B. (0;–1)

C. (–2; –1)                  D. (5; 6)

Câu 3: Tìm tập nghiệm của phương trình \({x^4} - 5{x^2} - 6 = 0.\) 

A. \(\left\{ { - 1;\,\,6} \right\}\)                   B. \(\left\{ { - \sqrt 6 ;\,\,\sqrt 6 } \right\}\)

C. \(\left\{ { - 1;\, - \sqrt 6 ;\,\,1;\,\,\sqrt 6 } \right\}\)      D. \(\left\{ {1;\,\,\sqrt 6 } \right\}\)

Câu 4: Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {x + 4}  - 1}}{{x - 1}}\,\,\,khi\,\,\,x > 4\\3 - x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,\,\,x \le 4\end{array} \right..\) Tính f (5) + f (–5).

A. \( - \dfrac{3}{2}\)                             B. \(\dfrac{{15}}{2}\)                          

C. \(\dfrac{{17}}{2}\)                              D. \( - \dfrac{5}{2}\)

Câu 5: Có tất cả bao nhiêu số nguyên m để phương trình \(4\sqrt {x - 2}  + {m^2}\sqrt {x + 2}  = 5\sqrt[4]{{{x^2} - 4}}\) có nghiệm.

A. 2                      B. 3

C. 1                      D. 4

Câu 6: Cho hình vuông ABCD có cạnh bằng a. Tích \(\overrightarrow {AB} .\overrightarrow {AC} \) bằng:

A. \(2{a^2}\)                    B. \({a^2}\) 

C. \({a^2}\sqrt 2 \)            D. 0

Câu 7: Cho \(\overrightarrow u \)= (1;-2) và \(\overrightarrow v \) = (-2;2). Khi đó \(2\overrightarrow u  + \overrightarrow v \) bằng:

A. (-2;1)               B. (-1;3) 

C. (0;-2)               D. (2;4)

Câu 8: Trong măt phẳng với hệ trục tọa độ \(\left( {O;\overrightarrow i ;\overrightarrow j } \right)\) cho các vectơ \(\overrightarrow u  = 2\overrightarrow i  - 3\overrightarrow j \) và \(\overrightarrow v  = k\overrightarrow i  + \dfrac{1}{3}\overrightarrow j \). Biết \(\overrightarrow u  \bot \overrightarrow v \), khi đó k bằng:

A. -4                     B. 4 

C. \(\dfrac{1}{2}\)                      D. \( - \dfrac{1}{2}\)

Câu 9: Cho tam giác ABC, lấy điểm M trên cạnh BC sao cho BM = 3MC. Biểu diễn \(\overrightarrow {AM} \) theo 2 vectơ \(\overrightarrow {AB} ,\,\,\overrightarrow {AC} \) ta được:

A. \(\overrightarrow {AM}  = \dfrac{3}{4}\overrightarrow {AB}  + \dfrac{1}{4}\overrightarrow {AC} \)

B. \(\overrightarrow {AM}  = \dfrac{1}{4}\overrightarrow {AB}  + \dfrac{3}{4}\overrightarrow {AC} \)

C. \(\overrightarrow {AM}  = \dfrac{4}{3}\overrightarrow {AB}  + \dfrac{1}{3}\overrightarrow {AC} \)

D. \(\overrightarrow {AM}  = \dfrac{1}{3}\overrightarrow {AB}  + \dfrac{4}{3}\overrightarrow {AC} \)

Câu 10: Tìm điều kiện của tham số m để phương trình \(\left( {5{m^2} - 4} \right)x = 2m + x\) có nghiệm.

A. \(m =  \pm 1\)

B. \(m =  \pm \dfrac{{\sqrt 5 }}{2}\)

C. \(m \ne  \pm \dfrac{{\sqrt 5 }}{2}\)

D. \(m \ne  \pm 1\)

Câu 11: Cho parabol \(\left( P \right):\,\,y = a{x^2} + bx + c\) có a < 0 và tọa độ đỉnh là (2;5). Tìm điều kiện của tham số m để phương trình \(a{x^2} + bx + c = m\) vô nghiệm.

A. m > 5

B. 2 < m < 5

C. m < 2

D. \(m \in \left\{ {2;5} \right\}\)

Câu 12: Cho tam giác đều ABC có cạnh bằng a. Khi đó \(\left| {\overrightarrow {AB}  + \overrightarrow {CA} } \right|\) bằng:

A. a            B. \(a\sqrt 3 \)

C. 2a          D. \(\dfrac{{a\sqrt 3 }}{2}\)

Câu 13: Gọi A, B là các giao điểm của đồ thị hàm số \(f\left( x \right) = 3{x^2} - 2\) và \(g\left( x \right) = 2{x^2} - x + 4\). Phương trình đường thẳng AB là:

A. y = –4x + 9

B. y = 3x – 12

C. y = –3x + 16

D. y = 4x – 11

Câu 14: Tìm số phần tử của tập hợp \(A = \left\{ {x \in \mathbb{Z}; - 3 < x \le 4} \right\}\).

A. 6                      B. 7

C. 8                      D. 5

Câu 15: Tìm giao điểm của parabol \(\left( P \right):\,\,y =  - {x^2} - 2x + 5\) với trục Oy.

A. (0;5)                B. (5;0)

C. (1;4)                D. (0;-5)

Câu 16: Cho tam giác ABC có AM là đường trung tuyến. Gọi I là trung điểm của AM. Trong các mệnh đề sau, mệnh đề nào đúng.

A. \(\overrightarrow {IA}  + \overrightarrow {IB}  + \overrightarrow {IC}  = \overrightarrow 0 \)

B. \(\overrightarrow {IA}  + 2\overrightarrow {IB}  + 2\overrightarrow {IC}  = \overrightarrow 0 \)

C. \(2\overrightarrow {IA}  + \overrightarrow {IB}  + \overrightarrow {IC}  = \overrightarrow 0 \)

D. \(2\overrightarrow {IA}  - \overrightarrow {IB}  - \overrightarrow {IC}  = \overrightarrow 0 \)

Câu 17: Cho tập hợp A gồm 3 phần tử. Hỏi tập hợp A có bao nhiêu tập con.

A. 4                      B. 8

C. 6                      D. 3

Câu 18: Cho hàm số \(y = \left( {m - 5} \right){x^2} - 5x + 1\). Hàm số đã cho là hàm số bậc nhất khi:

A. m = 5               B. m > 5

C. m < 5               D. \(m \ne 5\)

Câu 19: Hàm số nào dưới đây là hàm số chẵn trên tập xác định của nó?

A. \(y = \dfrac{4}{x}\)                  B. \(y = 4{x^3} - 2x\)

C. \(y = \sqrt {x + 1} \)

D. \(y =  - {x^4} + 3{x^2} + 1\)

Câu 20: Gọi S là tập hợp tất cả các giá trị của tham số m để đồ thị hàm số \(y = {x^2} + 5x + 2m\) cắt trục Ox tại hai điểm phân biệt A, B thỏa mãn OA = 4OB. Tổng các phần tử của S bằng:

A. \(\dfrac{{43}}{9}\)                           B. \(\dfrac{{68}}{9}\)

C. \( - \dfrac{{41}}{9}\)               D. \( - \dfrac{{32}}{9}\)

Câu 21: Xác định hàm số bậc hai \(y = a{x^2} - x + c\) biết đồ thị hàm số đi qua A(1;-2) và B(2;3).

A. \(y = 3{x^2} - x - 4\)

B. \(y = {x^2} - 3x + 5\)

C. \(y = 2{x^2} - x - 3\)

D. \(y =  - {x^2} - 4x + 3\)

Câu 22: Hàm số \(y =  - {x^2} + 5x - 6\) đồng biến trên khoảng nào dưới đây?

A. (3;4)                B. (2;3)

C. (1;4)                D. (1;2)

Câu 23: Cho đồ thị \(\left( P \right):\,\,y = {x^2} + 4x - 2\). Điểm nào dưới đây thuộc (P)?

A. (1;-3)               B. (3;18)

C. (-2;-6)              D. (-1;-4)

Câu 24: Gọi \({m_0}\) là giá trị của m để hệ phương trình \(\left\{ \begin{array}{l}x + 3y = m\\mx + y = m - \dfrac{2}{9}\end{array} \right.\) có vô số nghiệm. Khi đó

A. \({m_0} \in \left( {0;\dfrac{1}{2}} \right)\)                B. \({m_0} \in \left( {\dfrac{1}{2};2} \right)\)

C. \({m_0} \in \left( { - \dfrac{1}{2};0} \right)\) 

D. \({m_0} \in \left( { - 1; - \dfrac{1}{2}} \right)\)

Câu 25: Gọi \({x_1};\,{x_2}\) là các nghiệm của phương trình \({x^2} + 4x - 15 = 0\). Tính \(\left| {{x_1} - {x_2}} \right|\).

A. 8                      B. \(\sqrt {76} \)

C. 4                      D. \(\sqrt {56} \)

Câu 26: Đồ thị hàm số \(y = 3{x^2} + 4x - 1\) nhận đường thẳng nào dưới đây làm trục đối xứng?

A. \(x = \dfrac{4}{3}\)                 B. \(y = \dfrac{2}{3}\)

C. \(x =  - \dfrac{2}{3}\)               D. \(x =  - \dfrac{1}{3}\)

Câu 27: Tìm tập nghiệm của phương trình \(\sqrt {3{x^2} - 4x + 4}  = 3x + 2\).

A. \(\left\{ 0 \right\}\)                   B. \(\left\{ { - \dfrac{8}{3}} \right\}\)

C. \(\left\{ { - \dfrac{8}{3};0} \right\}\)               D. \(\emptyset \)

Câu 28: Tọa độ đỉnh của parabol \(\left( P \right):\,\,y =  - {x^2} + 2x - 3\) là:

A. (1;-2)               B. (-2;3)

C. (-1;2)               D. (2;-3)

Câu 29: Phát biểu nào dưới đây là mệnh đề sai?

A. 5 là ước của 125.  

B. 2020 chia hết cho 101.

C. 9 là số chính phương.

D. 91 là số nguyên tố.

Câu 30: Cho tập hợp A = {0;1;2;3;4} và B = {0;2;4;6;8}. Hỏi tập hợp \(\left( {A\backslash B} \right) \cup \left( {B\backslash A} \right)\) có bao nhiêu phần tử?

A. 7                                B. 4

C. 10                    D. 3

Câu 31: Đường thẳng đi qua hai điểm A(-1;4) và B(2;-7) có phương trình là:

A. 3x + 11y – 1 = 0

B. 11x + 3y + 1 = 0

C. 11x + 3y – 1 = 0

D. 3x + 11y + 1 = 0

Câu 32: Tìm tập hợp tất cả các giá trị của tham số m để hàm số \(y = \sqrt {{x^2} + {m^2}}  + \sqrt {{x^2} - m} \) có tập xác định là R.

A. R \ {0}             B. \(\left( {0; + \infty } \right)\)

C. \(\left[ {0; + \infty } \right)\)                 D. \(\left( { - \infty ;0} \right]\)

Câu 33: Trong mặt phẳng tọa độ Oxy, cho ba điểm A(-6;0), B(0;2) và C(-6;2). Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC.

A. (-2;0)               B. (-3;1)

C. (3;-1)               D. (-2;1)

Câu 34: Tìm tập xác định của hàm số \(y = \sqrt {x + 2}  - \dfrac{2}{{x - 3}}\).

A. R\{3}               B. \(\left( {3; + \infty } \right)\) 

C. \(\left( { - 2; + \infty } \right)\)              D. \(\left( { - 2; + \infty } \right]\backslash \left\{ 3 \right\}\)

Câu 35: Cho hình thoi ABCD có \(\angle BAD = {60^0}\) và BA = a. Gọi M, N lần lượt là trung điểm của AD, DC. Tính \(\overrightarrow {BM} .\overrightarrow {BN} \) bằng:

A. \(\dfrac{{3\sqrt 3 {a^2}}}{8}\)                               B. \(\dfrac{{3{a^2}}}{8}\)

C. \(\dfrac{{3{a^2}}}{4}\)                              D. \(\dfrac{{\sqrt 3 {a^2}}}{4}\)

Câu 36: Cho phương trình \({x^3} + 3{x^2} + \left( {4{m^2} - 12m + 11} \right)x + {\left( {2m - 3} \right)^2} = 0.\) Tập hợp tất cả các giá trị của tham số m để phương trình có 3 nghiệm phân biệt.

A. (1; 2)                   B. (–1; 1)

C. (–2; –1)               D. \(\left( { - \infty ;\,\,2} \right)\)

Câu 37: Cho tam giác ABC, lấy các điểm M, N trên cạnh BC sao cho BM = MN = NC. Gọi \({G_1},\,\,{G_2}\) lần lượt là trọng tâm tam giác ABN, ACM. Biết rằng \(\overrightarrow {{G_1}{G_2}} \) được biểu diễn theo hai vecto \(\overrightarrow {AB} ,\,\,\overrightarrow {AC} \) dưới dạng \(\overrightarrow {{G_1}{G_2}}  = x\overrightarrow {AB}  + y\overrightarrow {AC} .\) Khi đó x + y bằng:

A. \(\dfrac{4}{3}\)                                B. 1

C. \(\dfrac{2}{3}\)                                D. 0

Câu 38: Trong mặt phẳng tọa độ Oxy, cho các vecto \(\overrightarrow a  = \left( {3; - 1} \right),\,\,\overrightarrow b  = \left( {5; - 4} \right),\,\,\overrightarrow c  = \left( {1; - 5} \right).\) Biết \(\overrightarrow c  = x\overrightarrow a  + y\overrightarrow b .\) Tính x + y.

A. 2                                B. –5

C. 4                                D. –1

Câu 39: Cho hình chữ nhật ABCD có AB = a, AC = 2a. Tính góc giữa hai vecto \(\overrightarrow {CA} \) và \(\overrightarrow {DC} .\)

A. \({120^0}\)                            B. \({60^0}\)

C. \({150^0}\)                            D. \({45^0}\)

Câu 40: Hàm số nào dưới đây đồng biến trên tập \(\mathbb{R}?\)

A. \(y =  - 2 + 3x\)                       B. \(y = \dfrac{2}{x}\)

C. \(y = \sqrt {x + 3} \)                          D. \(y =  - x + 2\)

Câu 41: Cho hệ phương trình \(\left\{ \begin{array}{l}x - \left( {m + 1} \right)y = m - 2\\2mx + \left( {m - 2} \right)y = 4\end{array} \right.\). Biết rằng có hai giá trị của tham số m là m₁ và m₂ để hệ phương trình có nghiệm \(\left( {{x_0};2} \right)\). Tính m₁ + m­₂.

A. \(\dfrac{2}{3}\)                      B. \(\dfrac{7}{3}\)

C. \( - \dfrac{4}{3}\)                    D. \( - \dfrac{1}{3}\)

Câu 42: Phương trình \(\left| {3 - x} \right| = \left| {2x - 5} \right|\) có hai nghiệm \({x_1},\,\,{x_2}.\) Tính \({x_1} + {x_2}.\)

A. \( - \dfrac{{28}}{3}\)                         B. \(\dfrac{7}{3}\)

C. \( - \dfrac{{14}}{3}\)                         D. \(\dfrac{{14}}{3}\)

Câu 43: Có bao nhiêu giá trị nguyên của tham số m để phương trình \({\left( {{x^2} + 6x + 10} \right)^2} + m = 10{\left( {x + 3} \right)^2}\) có 4 nghiệm phân biệt?

A. 13                              B. 14

C. 15                              D. 16

Câu 44: Trong mặt phẳng tọa độ Oxy, cho các điểm A(4; 3), B(0; –1), C(1;–2). Tìm tọa độ điểm M biết rằng vetco \( - 2\overrightarrow {MA}  + 3\overrightarrow {MB}  - 3\overrightarrow {MC} \) có tọa độ là (1; 7).

A. (6; 5)                         B. (–2; –3)

C. (3; –1)                       D. (1; –2)

Câu 45: Cho phương trình \({x^2} + 2x - {m^2} = 0.\) Biết rằng có hai giá trị \({m_1},\,\,{m_2}\) của tham số m để phương trình có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^3 + x_2^3 + 10 = 0.\) Tính \({m_1}.{m_2}.\)

A. \(\dfrac{3}{4}\)                                B. \( - \dfrac{1}{3}\)

C. \( - \dfrac{3}{4}\)                             D. \(\dfrac{1}{3}\)

Câu 46: Trong mặt phẳng tọa độ Oxy, cho các điểm \(A\left( {m; - 1} \right),\,\,B\left( {2;\,\,1 - 2m} \right),\,\,C\left( {3m + 1; - \dfrac{7}{3}} \right).\) Biết rằng có hai giá trị \({m_1},\,\,{m_2}\) của tham số m để A, B, C thẳng hàng. Tính \({m_1} + {m_2}.\)

A. \( - \dfrac{1}{6}\)                             B. \( - \dfrac{4}{3}\)

C. \(\dfrac{{13}}{6}\)                                     D. \(\dfrac{1}{6}\)

Câu 47: Gọi (a; b; c) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}5x + y + z = 5\\x - 3y + 2z = 11\\ - x + 2y + z =  - 3\end{array} \right..\) Tính \({a^2} + {b^2} + {c^2}.\)

A. 9                                B. 16

C. 8                                D. 14

Câu 48: Tìm tập nghiệm của phương trình \(\sqrt {4x + 1}  + 5 = 0.\)

A. \(\left\{ 2 \right\}\)                             B. \(\emptyset \)

C. \(\left\{ { - \dfrac{1}{4}} \right\}\)                           D. \(\left\{ 6 \right\}\)

Câu 49: Trong mặt phẳng với hệ trục tọa độ \(\left( {O;\,\,\overrightarrow i ;\,\,\overrightarrow j } \right)\) cho điểm M thỏa mãn \(\overrightarrow {OM}  =  - 2\overrightarrow i  + 3\overrightarrow j .\) Tọa độ của M là:

A. (2; –3)                                 B. (–3; 2)

C. (–2; 3)                                 D. (3; –2)

Câu 50: Gọi M, N lần lượt là trung điểm các cạnh CD, AB của hình bình hành ABCD. Tìm mệnh đề đúng trong các mệnh đề sau:

A. \(\overrightarrow {AM} .\overrightarrow {DN}  = \dfrac{1}{4}A{B^2} - A{D^2}\) 

B. \(\overrightarrow {AM} .\overrightarrow {DN}  = \dfrac{1}{4}A{B^2} + A{D^2}\)

C. \(\overrightarrow {AM} .\overrightarrow {DN}  = A{B^2} - \dfrac{1}{4}A{D^2}\)  

D. \(\overrightarrow {AM} .\overrightarrow {DN}  = A{B^2} + \dfrac{1}{4}A{D^2}\)

ĐÁP ÁN

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn Loigiahay.com

Câu 1 (NB)

Phương pháp

Hai phương trình tương đương là hai phương trình có cùng tập nghiệm.

Hướng dẫn giải:

Ta có: \({x^2} = 4 \Leftrightarrow \left| x \right| = 2\)

\( \Rightarrow \) Đáp án A đúng.

Đáp án  A.

Câu 2 (TH)

Phương pháp

Tứ giác ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AB}  = \overrightarrow {DC}  \Leftrightarrow \left\{ \begin{array}{l}{x_B} - {x_A} = {x_C} - {x_D}\\{y_B} - {y_A} = {y_C} - {y_D}\end{array} \right..\)

Hướng dẫn giải:

Gọi D(a; b). Khi đó ta có: ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AB}  = \overrightarrow {DC} \)

\(\begin{array}{l} \Leftrightarrow \left( {1;\,\,6} \right) = \left( { - 1 - a;\,\,5 - b} \right)\\ \Leftrightarrow \left\{ \begin{array}{l} - 1 - a = 1\\5 - b = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 2\\b =  - 1\end{array} \right. \Rightarrow D\left( { - 2; - 1} \right).\end{array}\)

Đáp án  C.

Câu 3 (TH)

Phương pháp

Giải phương trình \(a{x^4} + b{x^2} + c = 0\,\,\,\left( {a \ne 0} \right)\) bằng cách đặt ẩn phụ: \(t = {x^2}\,\,\,\left( {t \ge 0} \right).\)

Khi đó ta có phương trình \(a{t^2} + bt + c = 0.\)

Giải phương trình bậc hai ẩn t sau đó tìm x.

Hướng dẫn giải:

Đặt \({x^2} = t\,\,\left( {t \ge 0} \right).\) Khi đó ta có phương trình:

\(\begin{array}{l}{t^2} - 5t - 6 = 0 \Leftrightarrow \left( {t + 1} \right)\left( {t - 6} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}t + 1 = 0\\t - 6 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t =  - 1\,\,\left( {ktm} \right)\\t = 6\,\,\,\left( {tm} \right)\end{array} \right.\\ \Leftrightarrow {x^2} = 6 \Leftrightarrow \left[ \begin{array}{l}x = \sqrt 6 \\x =  - \sqrt 6 \end{array} \right..\end{array}\)

Vậy tập nghiệm của phương trình là:\(S = \left\{ { - \sqrt 6 ;\,\,\sqrt 6 } \right\}.\)

Đáp án B.

Câu 4 (TH)

Phương pháp

Thay các giá trị x = 5 và x =  – 5  vào hàm số f (x) tương ứng rồi tính giá trị biểu thức.

Hướng dẫn giải:

Ta có:\(\left\{ \begin{array}{l}f\left( 5 \right) = \dfrac{{\sqrt {5 + 4}  - 1}}{{5 - 1}} = \dfrac{1}{2}\\f\left( { - 5} \right) = 3 - \left( { - 5} \right) = 8\end{array} \right.\) \( \Rightarrow f\left( 5 \right) + f\left( { - 5} \right) = \dfrac{1}{2} + 8 = \dfrac{{17}}{2}.\)

Đáp án  C.

Câu 5 (VDC):

Phương pháp:

Giải phương trình bằng cách chia cả 2 vế cho \(\sqrt[4]{{x - 2}}\sqrt[4]{{x + 2}}\).

Hướng dẫn giải

ĐK: \(\left\{ \begin{array}{l}x - 2 \ge 0\\x + 2 \ge 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\x \ge  - 2\end{array} \right.\) \( \Leftrightarrow x \ge 2\) \( \Rightarrow D = \left[ {2; + \infty } \right)\).

\(\begin{array}{l}\,\,\,\,\,4\sqrt {x - 2}  + {m^2}\sqrt {x + 2}  = 5\sqrt[4]{{{x^2} - 4}}\\ \Leftrightarrow 4\sqrt {x - 2}  + {m^2}\sqrt {x + 2}  = 5\sqrt[4]{{x - 2}}\sqrt[4]{{x + 2}}\end{array}\)

TH1: \(x = 2\), phương trình trở thành: \(2{m^2} = 0 \Leftrightarrow m = 0\).

Thử lại với \(m = 0\) ta có:

\(\begin{array}{l}4\sqrt {x - 2}  = 5\sqrt[4]{{x - 2}}\sqrt[4]{{x + 2}}\\ \Leftrightarrow \sqrt[4]{{x - 2}}\left( {4\sqrt[4]{{x - 2}} - 5\sqrt[4]{{x + 2}}} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\,\,\left( {tm} \right)\\4\sqrt[4]{{x - 2}} - 5\sqrt[4]{{x + 2}} = 0\end{array} \right.\end{array}\)

Do đó phương trình có nghiệm \(x = 2\), suy ra \(m = 0\) thỏa mãn.

TH2: \(x \ne 2\), chia cả 2 vế của phương trình cho \(\sqrt[4]{{x - 2}}\sqrt[4]{{x + 2}}\) ta được: \(4\dfrac{{\sqrt[4]{{x - 2}}}}{{\sqrt[4]{{x + 2}}}} + {m^2}\dfrac{{\sqrt[4]{{x + 2}}}}{{\sqrt[4]{{x - 2}}}} = 5\)

Đặt \(\dfrac{{\sqrt[4]{{x - 2}}}}{{\sqrt[4]{{x + 2}}}} = t\,\,\left( {0 < t < 1} \right)\), phương trình trở thành \(4t + \dfrac{{{m^2}}}{t} = 5\)\( \Leftrightarrow 4{t^2} - 5t + {m^2} = 0\) (*)

Phương trình (*) có nghiệm \( \Leftrightarrow \Delta  = 25 - 16{m^2} \ge 0 \Leftrightarrow  - \dfrac{5}{4} \le m \le \dfrac{5}{4}\).

Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 1;0;1} \right\}\).

Thử lại:

Với \(m =  \pm 1\) ta có: \(4{t^2} - 4t + 1 = 0 \Leftrightarrow t = \dfrac{1}{2}\).

\(\begin{array}{l} \Rightarrow \dfrac{{\sqrt[4]{{x - 2}}}}{{\sqrt[4]{{x + 2}}}} = \dfrac{1}{2}\\ \Leftrightarrow 2\sqrt[4]{{x - 2}} = \sqrt[4]{{x + 2}}\\ \Leftrightarrow 16\left( {x - 2} \right) = x + 2\\ \Leftrightarrow 16x - 32 = x + 2\\ \Leftrightarrow 15x = 34\\ \Leftrightarrow x = \dfrac{{34}}{{15}}\,\,\left( {tm} \right)\end{array}\)

\( \Rightarrow m =  \pm 1\) thỏa mãn.

Vậy có 3 giá trị nguyên của m thỏa mãn yêu cầu bài toán là \(m \in \left\{ { - 1;0;1} \right\}\).

Đáp án B.

Câu 6 (TH):

Phương pháp:

Sử dụng công thức \(\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ;\overrightarrow b } \right)\).

Hướng dẫn giải

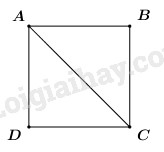
Vì ABCD là hình vuông cạnh a nên AB = BC = a và AC là phân giác của góc BAD.

\( \Rightarrow \angle BAC = {45^0} = \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right)\).

Áp dụng định lí Pytago trong tam giác vuông ABC ta có:

\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2}\\A{C^2} = {a^2} + {a^2} = 2{a^2}\\ \Rightarrow AC = a\sqrt 2 \end{array}\)

Vậy \(\overrightarrow {AB} .\overrightarrow {AC}  = AB.AC.\cos \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right)\) \( = a.a\sqrt 2 .\cos {45^0}\)\( = {a^2}\sqrt 2 .\dfrac{{\sqrt 2 }}{2}\) \( = {a^2}\).

Đáp án B.

Câu 7 (TH):

Phương pháp:

Sử dụng các công thức cộng vectơ và nhân véctơ với 1 số.

\(\begin{array}{l}\overrightarrow a  = \left( {{x_1};{y_1}} \right);\,\,\overrightarrow b  = \left( {{x_2};{y_2}} \right)\\ \Rightarrow k\overrightarrow a  = \left( {k{x_1};k{y_1}} \right)\\\,\,\,\,\,\,\,\overrightarrow a  + \overrightarrow b  = \left( {{x_1} + {x_2};{y_1} + {y_2}} \right)\end{array}\)

Hướng dẫn giải

Ta có

\(\begin{array}{l}2\overrightarrow u  = \left( {2; - 4} \right)\\\,\,\,\overrightarrow v  = \left( { - 2;2} \right)\\ \Rightarrow 2\overrightarrow u  + \overrightarrow v  = \left( {0; - 2} \right)\end{array}\)

Đáp án C.

Câu 8 (TH):

Phương pháp:

- Xác định tọa độ các vectơ \(\overrightarrow u ,\,\,\overrightarrow v \) như sau: \(\overrightarrow u  = x\overrightarrow i  + y\overrightarrow j \) \( \Rightarrow \overrightarrow u \left( {x;y} \right)\).

- \(\overrightarrow u  \bot \overrightarrow v  \Leftrightarrow \overrightarrow u .\overrightarrow v  = 0\).

Hướng dẫn giải

Ta có: \(\overrightarrow u  = 2\overrightarrow i  - 3\overrightarrow j  \Rightarrow \overrightarrow u \left( {2; - 3} \right)\) và \(\overrightarrow v  = k\overrightarrow i  + \dfrac{1}{3}\overrightarrow j  \Rightarrow \overrightarrow v \left( {k;\dfrac{1}{3}} \right)\).

Vì \(\overrightarrow u  \bot \overrightarrow v \) nên \(\overrightarrow u .\overrightarrow v  = 0\)

\(\begin{array}{l} \Leftrightarrow 2k - 3.\dfrac{1}{3} = 0\\ \Leftrightarrow 2k - 1 = 0\\ \Leftrightarrow k = \dfrac{1}{2}\end{array}\)

Đáp án C.

Câu 9 (TH):

Phương pháp:

Sử dụng quy tắc 3 điểm để cộng vectơ.

Hướng dẫn giải

\(\begin{array}{l}\overrightarrow {AM}  = \overrightarrow {AB}  + \overrightarrow {BM} \\\overrightarrow {AM}  = \overrightarrow {AB}  + \dfrac{3}{4}\overrightarrow {BC} \\\overrightarrow {AM}  = \overrightarrow {AB}  + \dfrac{3}{4}\left( {\overrightarrow {BA}  + \overrightarrow {AC} } \right)\\\overrightarrow {AM}  = \overrightarrow {AB}  - \dfrac{3}{4}\overrightarrow {AB}  + \dfrac{3}{4}\overrightarrow {AC} \\\overrightarrow {AM}  = \dfrac{1}{4}\overrightarrow {AB}  + \dfrac{3}{4}\overrightarrow {AC} \end{array}\)

Đáp án B.

Câu 10 (TH):

Phương pháp:

- Đưa phương trình về dạng phương trình bậc nhất một ẩn: ax + b = 0.

- Phương trình dạng ax + b = 0 có nghiệm \( \Leftrightarrow a \ne 0\).

Hướng dẫn giải

Ta có:

\(\begin{array}{l}\,\,\,\,\,\,\left( {5{m^2} - 4} \right)x = 2m + x\\ \Leftrightarrow \left( {5{m^2} - 4} \right)x - 2m - x = 0\\ \Leftrightarrow \left( {5{m^2} - 5} \right)x - 2m = 0\end{array}\)

Phương trình trên có nghiệm

\(\begin{array}{l} \Leftrightarrow 5{m^2} - 5 \ne 0\\ \Leftrightarrow 5\left( {{m^2} - 1} \right) \ne 0\\ \Leftrightarrow {m^2} \ne 1\\ \Leftrightarrow m \ne  \pm 1\end{array}\) 

Đáp án D.

Câu 11 (TH):

Phương pháp:

- Xác định giá trị lớn nhất \(a\) của hàm số.

- Phương trình \(a{x^2} + bx + c = m\) có \(VT \le 5\) vô nghiệm \( \Leftrightarrow m > 5\).

Hướng dẫn giải

\(\left( P \right):\,\,y = a{x^2} + bx + c\) có a < 0 và tọa độ đỉnh là (2;5) hàm số đạt giá trị lớn nhất bằng 5 khi x = 2.

Do đó \(a{x^2} + bx + c \le 5\,\,\forall x\).

Vậy phương trình \(a{x^2} + bx + c = m\) vô nghiệm khi và chỉ khi m > 5.

Đáp án A.

Câu 12 (NB):

Phương pháp:

Sử dụng quy tắc 3 điểm để cộng vectơ.

Hướng dẫn giải

Ta có:

\(\left| {\overrightarrow {AB}  + \overrightarrow {CA} } \right| = \left| {\overrightarrow {CA}  + \overrightarrow {AB} } \right|\)\( = \left| {\overrightarrow {CB} } \right| = BC = a\).

Đáp án A.

Câu 13 (TH):

Phương pháp:

- Giải phương trình hoành độ giao điểm để tìm tọa độ các điểm A, B.

- Gọi phương trình đường thẳng AB là y = ax + b. Thay tọa độ các điểm A, B vào và tìm a, b.

Hướng dẫn giải

Xét phương trình hoành độ giao điểm:

\(\begin{array}{l}\,\,\,\,\,\,3{x^2} - 2 = 2{x^2} - x + 4\\ \Leftrightarrow {x^2} + x - 6 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\x =  - 3\end{array} \right.\end{array}\)

Với x = 2 thì y = 10 => A(2;10).

Với x = -3 thì y = 25 => B(-3;25).

Gọi phương trình đường thẳng AB là y = ax + b.

Vì \(A \in AB\) nên 10 = 2a + b.

Vì \(B \in AB\) nên 25 = -3a + b.

Ta có hệ phương trình

\(\left\{ \begin{array}{l}2a + b = 10\\ - 3a + b = 25\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 3\\b = 16\end{array} \right.\)

Vậy phương trình đường thẳng AB là y = –3x + 16.

Đáp án C.

Câu 14 (NB):

Phương pháp:

Viết tập hợp A dưới dạng liệt kê các phần tử và đếm số phần tử của A.

Hướng dẫn giải

\(A = \left\{ {x \in \mathbb{Z}; - 3 < x \le 4} \right\}\) \( \Rightarrow A = \left\{ { - 2; - 1;0;1;2;3;4} \right\}\).

Vậy tập hợp A có 7 phần tử.

Đáp án B.

Câu 15 (NB):

Phương pháp:

Tìm giao điểm của đồ thị hàm số với trục Oy ta cho x = 0.

Hướng dẫn giải

Cho x = 0 ta có: \(y =  - {0^2} - 2.0 + 5 = 5\).

Vậy giao điểm của (P) với Oy là (0;5).

Đáp án A.

Câu 16 (TH):

Phương pháp:

Sử dụng các đẳng thức vectơ liên quan đến trung điểm:

- Nếu I là trung điểm của AB thì \(\overrightarrow {IA}  + \overrightarrow {IB}  = \overrightarrow 0 \).

- Với mọi điểm M, I là trung điểm của AB thì \(\overrightarrow {MA}  + \overrightarrow {MB}  = 2\overrightarrow {MI} \).

Hướng dẫn giải

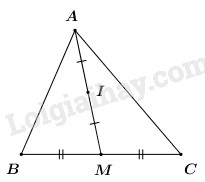
Vì I là trung điểm của AM nên \(\overrightarrow {IA}  + \overrightarrow {IM}  = \overrightarrow 0 \).

Mà M là trung điểm của BC nên \(\overrightarrow {IB}  + \overrightarrow {IC}  = 2\overrightarrow {IM} \).

Do đó \(\overrightarrow {IB}  + \overrightarrow {IC}  = -2\overrightarrow {IA} \) hay \(2\overrightarrow {IA}  + \overrightarrow {IB}  + \overrightarrow {IC}  = \overrightarrow 0 \).

Đáp án C.

Câu 17 (NB):

Phương pháp:

Tập hợp có n phần tử thì có \({2^n}\) tập hợp con.

Hướng dẫn giải

Tập hợp A có 2 phần tử nên có \({2^2} = 4\) tập con.

Đáp án A.

Câu 18 (NB):

Phương pháp:

Hàm số bậc nhất có dạng y = ax + b với \(a \ne 0\).

Hướng dẫn giải

Hàm số \(y = \left( {m - 5} \right){x^2} - 5x + 1\) là hàm số bậc nhất

\( \Leftrightarrow m - 5 = 0 \Leftrightarrow m = 5\).

Đáp án A.

Câu 19 (TH):

Phương pháp:

Cho hàm số y = f(x) có tập xác định là D.

- Nếu \(\forall x \in D \Rightarrow  - x \in D\) và f(-x) = f(x) thì hàm số là hàm số chẵn.

- Nếu \(\forall x \in D \Rightarrow  - x \in D\) và f(-x) = –f(x) thì hàm số là hàm số chẵn.

Hướng dẫn giải

Xét đáp án D ta có:

TXĐ: D = R nên \(\forall x \in D \Rightarrow  - x \in D\).

Đặt \(y = f\left( x \right) =  - {x^4} + 3{x^2} + 1\) ta có:

\(\begin{array}{l}f\left( { - x} \right) =  - {\left( { - x} \right)^4} + 3{\left( { - x} \right)^2} + 1\\f\left( { - x} \right) =  - {x^4} + 3{x^2} + 1\\f\left( { - x} \right) = f\left( x \right)\end{array}\)

Vậy hàm số \(y =  - {x^4} + 3{x^2} + 1\) là hàm số chẵn.

Đáp án D.

Câu 20 (VD):

Phương pháp:

- Tìm điều kiện để phương trình hoành độ giao điểm có 2 nghiệm phân biệt.

- Áp dụng định lí Vi-ét.

Hướng dẫn giải

Xét phương trình hoành độ giao điểm \({x^2} + 5x + 2m = 0\) (*).

Để đồ thị hàm số \(y = {x^2} + 5x + 2m\) cắt trục Ox tại 2 điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt \( \Leftrightarrow \Delta  = 25 - 8m > 0\) \( \Leftrightarrow m < \dfrac{{25}}{8}\).

Gọi \({x_1};{x_2}\) là hai nghiệm phân biệt của phương trình (*) \( \Rightarrow A\left( {{x_1};0} \right)\) và \(B\left( {{x_2};0} \right)\).

Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - 5\\{x_1}{x_2} = 2m\end{array} \right.\) (**).

Theo bài ra ta có:

OA = 4OB

\( \Leftrightarrow \left| {{x_1}} \right| = 4\left| {{x_2}} \right| \Leftrightarrow \left[ \begin{array}{l}{x_1} = 4{x_2}\\ - {x_1} = 4{x_2}\end{array} \right.\)

TH1; \({x_1} = 4{x_2}\), thay vào hệ (**) ta có:

\(\left\{ \begin{array}{l}{x_2} + 4{x_2} = 5\\{x_2}.4{x_2} = 2m\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_2} = 1\\4 = 2m\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_2} = 1\\m = 2\,\,\left( {tm} \right)\end{array} \right.\).

TH2; \( - {x_1} = 4{x_2}\), thay vào hệ (**) ta có:

\(\left\{ \begin{array}{l}{x_2} - 4{x_2} = 5\\{x_2}.\left( { - 4{x_2}} \right) = 2m\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_2} =  - \dfrac{5}{3}\\ - \dfrac{{100}}{9} = 2m\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_2} =  - \dfrac{5}{3}\\m =  - \dfrac{{50}}{9}\,\,\left( {tm} \right)\end{array} \right.\).

\( \Rightarrow S = \left\{ {2; - \dfrac{{50}}{9}} \right\}\).

Vậy tổng các phần tử của S bằng \(2 + \left( { - \dfrac{{50}}{9}} \right) =  - \dfrac{{32}}{9}\).

Đáp án D.

Câu 21 (TH):

Phương pháp:

- Thay tọa độ 2 điểm A và B vào hàm số, thiết lập hệ 2 phương trình 2 ẩn a, c.

- Giải hệ phương trình tìm a và c.

Hướng dẫn giải

Vì A thuộc đồ thị hàm số nên \( - 2 = a - 1 + c \Leftrightarrow a + c =  - 1\).

Vì B thuộc đồ thị hàm số nên \(3 = 4a - 2 + c \Leftrightarrow 4a + c = 5\).

Ta có hệ phương trình

\(\left\{ \begin{array}{l}a + c =  - 1\\4a + c = 5\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 2\\c =  - 3\end{array} \right.\).

Vậy \(y = 2{x^2} - x - 3\).

Đáp án C.

Câu 22 (TH):

Phương pháp:

Cho hàm số \(y = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\).

- Nếu a > 0 thì hàm số đồng biến trên \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\).

- Nếu a < 0 thì hàm số đồng biến trên \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\) và nghịch biến trên \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\).

Hướng dẫn giải

Hàm số \(y =  - {x^2} + 5x - 6\) có \( - \dfrac{b}{{2a}} =  - \dfrac{5}{{2.(-1)}} = \dfrac{5}{2}\) và \(a =  - 1 < 0\) nên hàm số đồng biến trên \(\left( { - \infty ;\dfrac{5}{2}} \right)\) và nghịch biến trên \(\left( {\dfrac{5}{2}; + \infty } \right)\).

Ta thấy \(\left( {1;2} \right) \subset \left( { - \infty ;\dfrac{5}{2}} \right)\) nên hàm số đồng biến trên (1;2).

Đáp án D.

Câu 23 (NB):

Phương pháp:

Thay tọa độ các điểm vào hàm số, điểm nào thỏa mãn thì sẽ thuộc đồ thị hàm số.

Hướng dẫn giải

Đáp án A: \({1^2} + 4.1 - 2 = 3 \ne  - 3 \Rightarrow \left( {1; - 3} \right)\) không thuộc (P).

Đáp án B: \({3^2} + 4.3 - 2 = 19 \ne 18 \Rightarrow \left( {3;18} \right)\) không thuộc (P).

Đáp án C: \({\left( { - 2} \right)^2} + 4.\left( { - 2} \right) - 2 =  - 6 \Rightarrow \left( { - 2; - 6} \right)\) thuộc (P).

Đáp án C.

Câu 24 (TH):

Phương pháp:

Hệ phương trình \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) có vô số nghiệm \( \Leftrightarrow \dfrac{a}{{a'}} = \dfrac{b}{{b'}} = \dfrac{c}{{c'}}\).

Hướng dẫn giải

Với m = 0, hệ phương trình trở thành \(\left\{ \begin{array}{l}x + 3y = 0\\y =  - \dfrac{2}{9}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{2}{3}\\y =  - \dfrac{2}{9}\end{array} \right.\).

Hệ phương trình có nghiệm duy nhất nên m = 0 loại.

Với \(m \ne 0\).

Hệ phương trình \(\left\{ \begin{array}{l}x + 3y = m\\mx + y = m - \dfrac{2}{9}\end{array} \right.\) có vô số nghiệm

\( \Leftrightarrow \dfrac{m}{1} = \dfrac{1}{3} = \dfrac{{m - \dfrac{2}{9}}}{m} \Leftrightarrow \left\{ \begin{array}{l}m = \dfrac{1}{3}\\{m^2} = m - \dfrac{2}{9}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m = \dfrac{1}{3}\\\left[ \begin{array}{l}m = \dfrac{2}{3}\\m = \dfrac{1}{3}\end{array} \right.\end{array} \right.\)\( \Leftrightarrow m = \dfrac{1}{3}\) (tm).

Vậy \({m_0} = \dfrac{1}{3} \Rightarrow {m_0} \in \left( {0;\dfrac{1}{2}} \right)\).

Đáp án A.

Câu 25 (TH):

Phương pháp:

Sử dụng định lí Vi-ét và biến đổi \(\left| {{x_1} - {x_2}} \right| = \sqrt {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \).

Hướng dẫn giải

Do \({x_1};\,{x_2}\) là các nghiệm của phương trình \({x^2} + 4x - 15 = 0\) nên áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - 4\\{x_1}{x_2} =  - 15\end{array} \right.\).

Vậy \(\left| {{x_1} - {x_2}} \right| = \sqrt {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \)\( = \sqrt {{{\left( { - 4} \right)}^2} - 4.\left( { - 15} \right)} \)\( = \sqrt {76} \).

Đáp án B.

Câu 26 (NB):

Phương pháp:

Đồ thị hàm số \(y = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\) nhận đường thẳng \(x =  - \dfrac{b}{{2a}}\) làm trục đối xứng.

Hướng dẫn giải

Đồ thị hàm số \(y = 3{x^2} + 4x - 1\) nhận đường thẳng \(x =  - \dfrac{4}{{2.3}} =  - \dfrac{2}{3}\) làm trục đối xứng.

Đáp án C.

Câu 27 (VD):

Phương pháp:

Giải phương trình chứa căn: \(\sqrt A  = B \Leftrightarrow \left\{ \begin{array}{l}B \ge 0\\A = {B^2}\end{array} \right.\).

Hướng dẫn giải

\(\begin{array}{l}\,\,\,\,\,\,\sqrt {3{x^2} - 4x + 4}  = 3x + 2\\ \Leftrightarrow \left\{ \begin{array}{l}3x + 2 \ge 0\\3{x^2} - 4x + 4 = {\left( {3x + 2} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge  - \dfrac{2}{3}\\3{x^2} - 4x + 4 = 9{x^2} + 12x + 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge  - \dfrac{2}{3}\\6{x^2} + 16x = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge  - \dfrac{2}{3}\\\left[ \begin{array}{l}x =  - \dfrac{8}{3}\\x = 0\end{array} \right.\end{array} \right.\\ \Leftrightarrow x = 0\end{array}\)

Vậy tập nghiệm của phương trình là \(S = \left\{ 0 \right\}\).

Đáp án A.

Câu 28 (NB):

Phương pháp:

\(\left( P \right):\,\,y = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\) có đỉnh \(I\left( { - \dfrac{b}{{2a}}; - \dfrac{\Delta }{{4a}}} \right)\).

Hướng dẫn giải

Hàm số  \(\left( P \right):\,\,y =  - {x^2} + 2x - 3\) có các hệ số \(a =  - 1,\,\,\,b = 2,\,\,c =  - 3\).

\( \Rightarrow  - \dfrac{b}{{2a}} =  - \dfrac{2}{{2.\left( { - 1} \right)}} = 1\) và \( - \dfrac{\Delta }{{4a}} =  - 2\).

Vậy đỉnh của parabol là \(I\left( {1; - 2} \right)\).

Đáp án A.

Câu 29 (NB):

Phương pháp:

Nhận xét từng đáp án.

Hướng dẫn giải

Ta có 91 = 7.13 nên 91 là hợp số.

Vậy đáp án D sai.

Đáp án D.

Câu 30 (TH):

Phương pháp:

- Tính \(A\backslash B = \left\{ {x|x \in A,\,\,x \notin B} \right\}\).

- Tính \(B\backslash A = \left\{ {x|x \in B;\,\,x \notin A} \right\}\).

- Tính \(\left( {A\backslash B} \right) \cup \left( {B\backslash A} \right) = \left\{ {x|x \in A\backslash B\,\,hoac\,\,x \in B\backslash A} \right\}\)

Hướng dẫn giải

Ta có:

A \ B = {1;3} ,  B \ A = {6;8}

\( \Rightarrow \left( {A\backslash B} \right) \cup \left( {B\backslash A} \right) = \left\{ {1;3;6;8} \right\}\).

Vậy \(\left( {A\backslash B} \right) \cup \left( {B\backslash A} \right)\) có 4 phần tử.

Đáp án B.

Câu 31 (TH):

Phương pháp:

Gọi phương trình đường thẳng AB là y = ax + b. Thay tọa độ các điểm A, B vào và tìm a, b.

Hướng dẫn giải

Gọi phương trình đường thẳng AB là y = ax + b.

Vì \(A \in AB\) nên 4 = –a + b.

Vì \(B \in AB\) nên –7 = 2a + b.

Ta có hệ phương trình

\(\left\{ \begin{array}{l} - a + b = 4\\2a + b =  - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - \dfrac{{11}}{3}\\b = \dfrac{1}{3}\end{array} \right.\)

Vậy phương trình đường thẳng AB là \(y =  - \dfrac{{11}}{3}x + \dfrac{1}{3}\) \( \Leftrightarrow 3y =  - 11x + 1\)\( \Leftrightarrow 11x + 3y - 1 = 0\).

Đáp án C.

Câu 32 (VD):

Phương pháp:

\(\sqrt A \) xác định \( \Leftrightarrow A \ge 0\).

Hướng dẫn giải

Hàm số xác định

\( \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {m^2} \ge 0\,\,\\{x^2} - m \ge 0\end{array} \right. \Leftrightarrow {x^2} \ge m\).

Để hàm số xác định trên R thì \({x^2} \ge m\,\,\forall x \in R\).

Mà \({x^2} \ge 0\,\,\forall x \Rightarrow m \le 0\).

Vậy \(m \in \left( { - \infty ;0} \right]\).

Đáp án D.

Câu 33 (VD):

Phương pháp:

- Gọi I là tâm đường tròn ngoại tiếp tam giác ABC thì IA = IB = IC.

- Sử dụng công thức tính độ dài đoạn thẳng \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \).

Hướng dẫn giải

Gọi I(x;y) là tâm đường tròn ngoại tiếp tam giác ABC thì IA = IB = IC.

\(\begin{array}{l} \Rightarrow I{A^2} = I{B^2} = I{C^2}\\ \Rightarrow \left\{ \begin{array}{l}I{A^2} = I{B^2}\\I{A^2} = I{C^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{\left( { - 6 - x} \right)^2} + {\left( { - y} \right)^2} = {\left( { - x} \right)^2} + {\left( {2 - y} \right)^2}\\{\left( { - 6 - x} \right)^2} + {\left( { - y} \right)^2} = {\left( { - 6 - x} \right)^2} + {\left( {2 - y} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x^2} + 12x + 36 + {y^2} = {x^2} + {y^2} - 4y + 4\\{y^2} = {y^2} - 4y + 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}12x + 4y =  - 32\\ - 4y + 4 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x =  - 3\\y = 1\end{array} \right.\end{array}\)

Vậy I(-3;1).

Đáp án B.

Câu 34 (TH):

Phương pháp:

\(\sqrt A \) xác định \( \Leftrightarrow A \ge 0\).

\(\dfrac{1}{A}\) xác định \( \Leftrightarrow A \ne 0\).

Hướng dẫn giải

Hàm số xác định \( \Leftrightarrow \left\{ \begin{array}{l}x + 2 \ge 0\\x - 3 \ne 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge -2\\x \ne 3\end{array} \right.\).

Vậy tập xác định của hàm số là \(D = \left( { - 2; + \infty } \right]\backslash \left\{ 3 \right\}\).

Đáp án D.

Câu 35 (VD)

Phương pháp

Sử dụng công thức tính tích vô hướng: \(\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\,\,\overrightarrow b } \right).\)

Hướng dẫn giải:

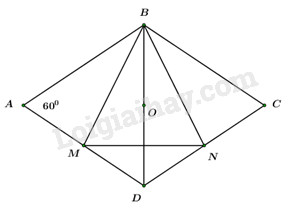
Ta có: ABCD là hình thoi có \(\angle BAD = {60^0}\)\( \Rightarrow \angle ABC = {120^0}\) và tam giác ABD là tam giác đều.

\( \Rightarrow AB = AD = BD = a.\)

Áp dụng quy tắc hình bình hành ta có: \(\left\{ \begin{array}{l}\overrightarrow {BM}  = \dfrac{1}{2}\left( {\overrightarrow {BA}  + \overrightarrow {BD} } \right)\\\overrightarrow {BN}  = \dfrac{1}{2}\left( {\overrightarrow {BD}  + \overrightarrow {BC} } \right)\end{array} \right..\)

\(\begin{array}{l} \Rightarrow \overrightarrow {BM} .\overrightarrow {BN}  = \dfrac{1}{4}\left( {\overrightarrow {BA}  + \overrightarrow {BD} } \right)\left( {\overrightarrow {BD}  + \overrightarrow {BC} } \right)\\ = \dfrac{1}{4}\left( {\overrightarrow {BA} .\overrightarrow {BD}  + \overrightarrow {BA} .\overrightarrow {BC}  + {{\overrightarrow {BD} }^2} + \overrightarrow {BD} .\overrightarrow {BC} } \right)\\ = \dfrac{1}{4}\left( {BA.BD.\cos ABD + BA.BC.\cos ABC + B{D^2} + BD.BC.\cos DBC} \right)\\ = \dfrac{1}{4}\left( {{a^2}.\cos {{60}^0} + {a^2}.\cos {{120}^0} + {a^2} + {a^2}.\cos {{60}^0}} \right)\\ = \dfrac{1}{4}\left( {\dfrac{{{a^2}}}{2} - \dfrac{{{a^2}}}{2} + {a^2} + \dfrac{{{a^2}}}{2}} \right) = \dfrac{{3{a^2}}}{8}.\end{array}\)

Đáp án  B.

Câu 36 (VDC)

Phương pháp

Biến đổi phương trình đã cho về dạng:\(\left( {x - a} \right)g\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = a\\g\left( x \right) = 0\end{array} \right..\)

Phương trình đã cho có 3 nghiệm phân biệt \( \Leftrightarrow g\left( x \right) = 0\) có hai nghiệm phân biệt \( \ne a.\)

\( \Leftrightarrow \left\{ \begin{array}{l}\Delta  > 0\\g\left( a \right) \ne 0\end{array} \right..\)

Hướng dẫn giải:

\(\begin{array}{l}\,\,\,\,\,{x^3} + 3{x^2} + \left( {4{m^2} - 12m + 11} \right)x + {\left( {2m - 3} \right)^2} = 0\,\,\,\,\,\,\left( * \right)\\ \Leftrightarrow \,{x^3} + 3{x^2} + \left( {4{m^2} - 12m + 11} \right)x + 4{m^2} - 12m + 9 = 0\\ \Leftrightarrow {x^3} + {x^2} + 2{x^2} + 2x + \left( {4{m^2} - 12m + 9} \right)x + 4{m^2} - 12m + 9 = 0\\ \Leftrightarrow {x^2}\left( {x + 1} \right) + 2x\left( {x + 1} \right) + \left( {4{m^2} - 12m + 9} \right)\left( {x + 1} \right) = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} + 2x + 4{m^2} - 12m + 9} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\g\left( x \right) = {x^2} + 2x + 4{m^2} - 12m + 9 = 0\end{array} \right.\end{array}\)

Phương trình đã cho có 3 nghiệm phân biệt \( \Leftrightarrow g\left( x \right) = 0\) có hai nghiệm phân biệt \( \ne  - 1\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\g\left( { - 1} \right) \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 - 4{m^2} + 12m - 9 > 0\\{\left( { - 1} \right)^2} + 2\left( { - 1} \right) + 4{m^2} - 12m + 9 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}4{m^2} - 12m + 8 < 0\\4{m^2} - 12m + 8 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 < m < 2\\m \ne 2\\m \ne 1\end{array} \right. \Leftrightarrow 1 < m < 2.\end{array}\)

Đáp án  A.

Câu 37 (VD)

Phương pháp

Sử dụng các quy tắc vecto và các phép toán trên vecto để biến đổi và tìm x, y.

Hướng dẫn giải:

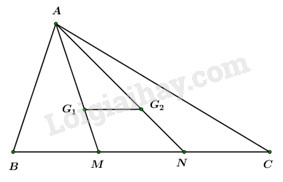
Ta có:\({G_1}\)  trọng tâm tam giác ABN \( \Rightarrow \overrightarrow {A{G_1}}  = \dfrac{2}{3}\overrightarrow {AM} .\)

\({G_2}\)  trọng tâm tam giác ACM \( \Rightarrow \overrightarrow {A{G_2}}  = \dfrac{2}{3}\overrightarrow {AN} .\)

\(\begin{array}{l} \Rightarrow \overrightarrow {{G_1}{G_2}}  = \overrightarrow {{G_1}A}  + \overrightarrow {A{G_2}}  =  - \dfrac{2}{3}\overrightarrow {AM}  + \dfrac{2}{3}\overrightarrow {AN} \\ =  - \dfrac{2}{3}\left( {\overrightarrow {AB}  + \overrightarrow {BM} } \right) + \dfrac{2}{3}\left( {\overrightarrow {AC}  + \overrightarrow {CN} } \right)\\ =  - \dfrac{2}{3}\overrightarrow {AB}  - \dfrac{2}{3}.\dfrac{1}{3}\overrightarrow {BC}  + \dfrac{2}{3}\overrightarrow {AC}  - \dfrac{2}{3}.\dfrac{1}{3}\overrightarrow {BC} \\ =  - \dfrac{2}{3}\overrightarrow {AB}  + \dfrac{2}{3}\overrightarrow {AC}  - \dfrac{4}{9}\overrightarrow {BC} \\ =  - \dfrac{2}{3}\overrightarrow {AB}  + \dfrac{2}{3}\overrightarrow {AC}  - \dfrac{4}{9}\left( {\overrightarrow {AC}  - \overrightarrow {AB} } \right)\\ =  - \dfrac{2}{3}\overrightarrow {AB}  + \dfrac{2}{3}\overrightarrow {AC}  - \dfrac{4}{9}\overrightarrow {AC}  + \dfrac{4}{9}\overrightarrow {AB} \\ =  - \dfrac{2}{9}\overrightarrow {AB}  + \dfrac{2}{9}\overrightarrow {AC} .\\ \Rightarrow \left\{ \begin{array}{l}x =  - \dfrac{2}{9}\\y = \dfrac{2}{9}\end{array} \right. \Rightarrow x + y =  - \dfrac{2}{9} + \dfrac{2}{9} = 0.\end{array}\)

Đáp án  D.

Câu 38 (VD)

Phương pháp

Cho các vecto \(\overrightarrow a  = \left( {{a_1};\,\,{a_2}} \right),\,\,\overrightarrow b  = \left( {{b_1};\,\,{b_2}} \right)\) và \(k \in \mathbb{R}\) ta có: \(\left\{ \begin{array}{l}\overrightarrow a  + \overrightarrow b  = \left( {{a_1} + {b_1};\,\,{a_2} + {b_2}} \right)\\k\overrightarrow a  = k\left( {{a_1};\,\,{a_2}} \right) = \left( {k{a_1};\,\,k{a_2}} \right)\end{array} \right..\)

Hướng dẫn giải:

Ta có: \(\overrightarrow c  = x\overrightarrow a  + y\overrightarrow b \)

\(\begin{array}{l} \Leftrightarrow \left( {1; - 5} \right) = x\left( {3; - 1} \right) + y\left( {5; - 4} \right)\\ \Leftrightarrow \left( {1; - 5} \right) = \left( {3x; - x} \right) + \left( {5y; - 4y} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}1 = 3x + 5y\\ - 5 =  - x - 4y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 3\\y = 2\end{array} \right.\\ \Rightarrow x + y =  - 3 + 2 =  - 1.\end{array}\)

Đáp án  D.

Câu 39 (TH)

Phương pháp

Sử dụng công thức tính góc giữa hai vecto: \(\cos \left( {\overrightarrow a ,\,\,\overrightarrow b } \right) = \dfrac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}.\)

Hướng dẫn giải:

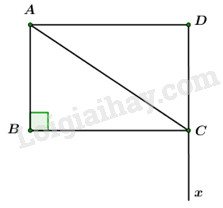
Ta có: ABCD là hình chữ nhật nên ta có: AB = DC = a.

\(\begin{array}{l}\angle \left( {\overrightarrow {CA} ,\,\,\overrightarrow {DC} } \right) = \angle \left( {\overrightarrow {CA} ,\,\,\overrightarrow {Cx} } \right) = \angle ACx = {180^0} - \angle ACD.\\ \Rightarrow \cos \angle ACD = \dfrac{{CD}}{{AC}} = \dfrac{a}{{2a}} = \dfrac{1}{2}\\ \Rightarrow \angle ACD = {60^0}\\ \Rightarrow \angle ACx = {180^0} - {60^0} = {120^0}.\end{array}\)

Đáp án A.

Câu 40 (TH)

Phương pháp

Hàm số: \(y = ax + b\,\,\,\left( {a \ne 0} \right)\) đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0.\)

Hướng dẫn giải:

+) Xét đáp án A: \(y =  - 2 + 3x\) có \(a = 3 > 0 \Rightarrow \) hàm số đồng biến trên \(\mathbb{R}.\)

Đáp án A.

Câu 41 (VD):

Phương pháp:

- Thay \(y = 2\) vào hệ phương trình.

- Rút x từ phương trình thứ nhất thế vào phương trình thứ hai, rút ra phương trình bậc hai ẩn m.

- Áp dụng định lí Vi-ét.

Hướng dẫn giải

Hệ phương trình có nghiệm \(\left( {{x_0};2} \right)\) nên thay \(y = 2\) ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}x - 2\left( {m + 1} \right) = m - 2\\2mx + 2\left( {m - 2} \right) = 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x - 2m - 2 = m - 2\\2mx + 2m - 4 = 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 3m\\2mx = 8 - 2m\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 3m\\2m.3m = 8 - 2m\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 3m\\6{m^2} + 2m - 8 = 0\,\,\left( 1 \right)\end{array} \right.\end{array}\)

Hai giá trị của tham số m là nghiệm của phương trình (1), do đó áp dụng định lí Vi-ét ta có \({m_1} + {m_2} = \dfrac{{ - 1}}{3}\).

Đáp án D.

Câu 42 (VD)

Phương pháp

Giải phương trình chứa dấu giá trị tuyệt đối: \(\left| {f\left( x \right)} \right| = g\left( x \right) \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = g\left( x \right)\\f\left( x \right) =  - g\left( x \right)\end{array} \right..\) 

Hướng dẫn giải:

Ta có: \(\left| {3 - x} \right| = \left| {2x - 5} \right|\)

\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}3 - x = 2x - 5\\3 - x =  - 2x + 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}3x = 8\\x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{8}{3}\\x = 2\end{array} \right.\\ \Rightarrow {x_1} + {x_2} = \dfrac{8}{3} + 2 = \dfrac{{14}}{3}.\end{array}\)

Đáp án  D.

Câu 43 (VDC)

Phương pháp

Biến đổi phương trình, đặt ẩn phụ rồi biện luận phương trình.

Hướng dẫn giải:

TXĐ: \(D = \mathbb{R}.\)

\(\begin{array}{l}\,\,\,\,\,\,{\left( {{x^2} + 6x + 10} \right)^2} + m = 10{\left( {x + 3} \right)^2}\,\,\,\,\\ \Leftrightarrow {\left( {{x^2} + 6x + 9 + 1} \right)^2} - 10{\left( {x + 3} \right)^2} + m = 0\\ \Leftrightarrow {\left[ {{{\left( {x + 3} \right)}^2} + 1} \right]^2} - 10{\left( {x + 3} \right)^2} + m = 0\\ \Leftrightarrow {\left( {x + 3} \right)^4} + 2{\left( {x + 3} \right)^2} + 1 - 10{\left( {x + 3} \right)^2} + m = 0\\ \Leftrightarrow {\left( {x + 3} \right)^4} - 8{\left( {x + 3} \right)^2} + m + 1 = 0\,\,\,\,\,\left( * \right)\end{array}\)

Đặt \({\left( {x + 3} \right)^2} = t\,\,\left( {t \ge 0} \right).\)

\( \Rightarrow \left( * \right) \Leftrightarrow {t^2} - 8t + m + 1 = 0\,\,\,\,\left( 1 \right)\)

\( \Rightarrow \left( * \right)\) có 4 nghiệm phân biệt \( \Leftrightarrow \left( 1 \right)\) có hai nghiệm  t dương phân biệt

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\ - \dfrac{b}{a} > 0\\\dfrac{c}{a} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}16 - m - 1 > 0\\8 > 0\\m + 1 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}15 - m > 0\\m >  - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 15\\m >  - 1\end{array} \right. \Leftrightarrow  - 1 < m < 15\end{array}\)

Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;\,\,1;\,\,2;\,\,.....;\,\,14} \right\}.\)

\( \Rightarrow \) Có 15 giá trị m thỏa mãn bài toán.

Đáp án  C.

Câu 44 (VD)

Phương pháp

Cho các vecto \(\overrightarrow a  = \left( {{a_1};\,\,{a_2}} \right),\,\,\overrightarrow b  = \left( {{b_1};\,\,{b_2}} \right)\) và \(k \in \mathbb{R}\) ta có: \(\left\{ \begin{array}{l}\overrightarrow a  + \overrightarrow b  = \left( {{a_1} + {b_1};\,\,{a_2} + {b_2}} \right)\\k\overrightarrow a  = k\left( {{a_1};\,\,{a_2}} \right) = \left( {k{a_1};\,\,k{a_2}} \right)\end{array} \right..\)

Hướng dẫn giải:

Gọi M (a; b).

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\overrightarrow {MA}  = \left( {4 - a;\,\,3 - b} \right)\\\overrightarrow {MB}  = \left( { - a; - 1 - b} \right)\\\overrightarrow {MC}  = \left( {1 - a; - 2 - b} \right)\end{array} \right. \\\Rightarrow  - 2\overrightarrow {MA}  + 3\overrightarrow {MB}  - 3\overrightarrow {MC}  = \left( {1;\,\,7} \right)\\ \Leftrightarrow  - 2\left( {4 - a;\,\,3 - b} \right) + 3\left( { - a; - 1 - b} \right) - 3\left( {1 - a; - 2 - b} \right) = \left( {1;\,\,7} \right)\\ \Leftrightarrow \left\{ \begin{array}{l} - 2\left( {4 - a} \right) + 3\left( { - a} \right) - 3\left( {1 - a} \right) = 1\\ - 2\left( {3 - b} \right) + 3\left( { - 1 - b} \right) - 3\left( { - 2 - b} \right) = 7\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 8 + 2a - 3a - 3 + 3a = 1\\ - 6 + 2b - 3 - 3b + 6 + 3b = 7\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}2a = 12\\2b = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 6\\b = 5\end{array} \right. \Rightarrow M\left( {6;\,\,5} \right).\end{array}\)

Đáp án  A.

Câu 45 (VD)

Phương pháp

Tìm điều kiện của m để phương trình có hai nghiệm phân biệt.

Áp dụng định lý Vi-et để tính giá trị biểu thức, từ đó xác định giá trị của m.

Hướng dẫn giải:

Phương trình đã cho có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0\)

\( \Leftrightarrow 1 + {m^2} > 0\,\,\,\forall m\)

\( \Rightarrow \) Phương trình đã cho luôn có hai nghiệm phân biệt \({x_1},\,{x_2}\) với mọi m.

Áp dụng định lý Vi-et ta có:\(\left\{ \begin{array}{l}{x_1} + {x_2} =  - 2\\{x_1}{x_2} =  - {m^2}\end{array} \right..\)

Theo đề bài ta có: \(x_1^3 + x_2^3 + 10 = 0\)

\(\begin{array}{l} \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right) + 10 = 0\\ \Leftrightarrow {\left( { - 2} \right)^3} - 3\left( { - {m^2}} \right)\left( { - 2} \right) + 10 = 0\\ \Leftrightarrow  - 8 - 6{m^2} + 10 = 0\\ \Leftrightarrow 6{m^2} = 2 \Leftrightarrow {m^2} = \dfrac{1}{3}\\ \Leftrightarrow \left[ \begin{array}{l}{m_1} =  - \dfrac{1}{{\sqrt 3 }}\\{m_2} = \dfrac{1}{{\sqrt 3 }}\end{array} \right. \Rightarrow {m_1}{m_2} =  - \dfrac{1}{{\sqrt 3 }}.\dfrac{1}{{\sqrt 3 }} =  - \dfrac{1}{3}.\end{array}\)

Đáp án  B.

Câu 46 (VD)

Phương pháp

Ba điểm  A, B, C thẳng hàng \( \Leftrightarrow \overrightarrow {AB}  = k\overrightarrow {AC} \,\,\,\left( {k \in \mathbb{R},\,\,k \ne 0} \right).\) 

Hướng dẫn giải:

Ta có: \(\left\{ \begin{array}{l}\overrightarrow {AB}  = \left( {2 - m;\,\,2 - 2m} \right)\\\overrightarrow {AC}  = \left( {2m + 1;\,\, - \dfrac{4}{3}} \right)\end{array} \right..\)

Ba điểm  A, B, C thẳng hàng \( \Leftrightarrow \overrightarrow {AB}  = k\overrightarrow {AC} \,\,\,\left( {k \in \mathbb{R},\,\,k \ne 0} \right)\) 

\(\begin{array}{l} \Leftrightarrow \left( {2 - m;\,\,2 - 2m} \right) = k\left( {2m + 1; - \dfrac{4}{3}} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}2 - m = k\left( {2m + 1} \right)\\2 - 2m =  - \dfrac{4}{3}k\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k = \dfrac{{3\left( {m - 1} \right)}}{2}\\2 - m = \dfrac{{3\left( {m - 1} \right)}}{2}\left( {2m + 1} \right)\,\,\,\,\left( * \right)\end{array} \right.\\ \Rightarrow \left( * \right) \Leftrightarrow 4 - 2m = 6{m^2} + 3m - 6m - 3\\ \Leftrightarrow 6{m^2} - m - 7 = 0\\ \Leftrightarrow \left( {6m - 7} \right)\left( {m + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}6m - 7 = 0\\m + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{7}{6}\\m =  - 1\end{array} \right.\\ \Rightarrow {m_1} + {m_2} = \dfrac{7}{6} - 1 = \dfrac{1}{6}.\end{array}\)

Đáp án  D.

Câu 47 (TH)

Phương pháp

Giải hệ phương trình bậc nhất ba ẩn sau đó tính giá trị của biểu thức.

Hướng dẫn giải:

Ta có:  \(\left\{ \begin{array}{l}5x + y + z = 5\\x - 3y + 2z = 11\\ - x + 2y + z =  - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y =  - 2\\z = 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 1\\b =  - 2\\c = 2\end{array} \right.\)\( \Rightarrow {a^2} + {b^2} + {c^2} = {1^2} + {\left( { - 2} \right)^2} + {2^2} = 9.\)

Đáp án  A.

Câu 48 (TH)

Phương pháp

Giải phương trình chứa căn bậc hai.

Hướng dẫn giải:

Điều kiện: \(4x + 1 \ge 0 \Leftrightarrow x \ge  - \dfrac{1}{4}.\)

Ta có: \(\sqrt {4x + 1}  \ge 0\,\,\forall x \ge  - \dfrac{1}{4}\) \( \Rightarrow \sqrt {4x + 1}  + 5 > 0\,\,\forall x \ge  - \dfrac{1}{4}\)

\( \Rightarrow \) Phương trình đã cho vô nghiệm.

Đáp án  B.

Câu 49 (TH)

Phương pháp

Cho  vetco \(\overrightarrow u  = a\overrightarrow i  + b\overrightarrow j  \Rightarrow \overrightarrow u  = \left( {a;\,\,b} \right).\)

Hướng dẫn giải:

Ta có: \(\overrightarrow {OM}  =  - 2\overrightarrow i  + 3\overrightarrow j  \Rightarrow \overrightarrow {OM}  = \left( { - 2;\,\,3} \right) \Rightarrow M\left( { - 2;\,\,3} \right).\)

Đáp án  C.

Câu 50 (VDC)

Phương pháp 

Sử dụng các quy tắc hình bình hành và công thức tính tích vô hướng. 

Hướng dẫn giải:

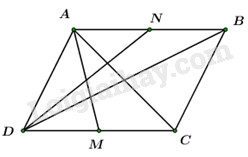
\(\begin{array}{l}\overrightarrow {AM} .\overrightarrow {DN}  = \left( {\overrightarrow {AD}  + \overrightarrow {DM} } \right)\left( {\overrightarrow {DA}  + \overrightarrow {AN} } \right)\\ = \overrightarrow {AD} .\overrightarrow {DA}  + \overrightarrow {DM} .\overrightarrow {DA}  + \overrightarrow {AD} .\overrightarrow {AN}  + \overrightarrow {DM} .\overrightarrow {AN} \\ =  - A{D^2} + \dfrac{1}{2}\overrightarrow {DC} .\overrightarrow {DA}  + \overrightarrow {AD} .\dfrac{1}{2}\overrightarrow {AB}  + \dfrac{1}{2}\overrightarrow {DC} .\dfrac{1}{2}\overrightarrow {AB} \\ =  - A{D^2} + \dfrac{1}{2}\overrightarrow {AB} .\overrightarrow {DA}  + \dfrac{1}{2}\overrightarrow {AD} .\overrightarrow {AB}  + \dfrac{1}{4}DC.AB.\cos {0^0}\\ =  - A{D^2} + \dfrac{1}{4}A{B^2}\\ = \dfrac{1}{4}A{B^2} - A{D^2}.\end{array}\)

Đáp án A.

Loigiaihay.com