 Toán 12 Kết nối tri thức | Giải toán lớp 12 Kết nối tri thức
Toán 12 Kết nối tri thức | Giải toán lớp 12 Kết nối tri thức
 Bài tập cuối chương 5 - Toán 12 Kết nối tri thức
Bài tập cuối chương 5 - Toán 12 Kết nối tri thức
Giải bài tập 5.52 trang 63 SGK Toán 12 tập 2 - Kết nối tri thức
Nếu đứng trước biển và nhìn ra xa, người ta sẽ thấy một đường giao giữa mặt biển và bầu trời, đó là đường chân trời đối với người quan sát (H.5.45a). Về mặt Vật lí, đường chân trời là đường giới hạn phần Trái Đất mà người quan sát có thể nhìn thấy được (phần còn lại bị chính Trái Đất che khuất). Ta có thể hình dung rằng, nếu người quan sát ở tại đỉnh một chiếc nón và Trái Đất được “thả” vào trong chiếc nón đó, thì đường chân trời trong trường hợp này là đường chạm giữa Trái Đất và chiếc nón (H.5
Đề bài
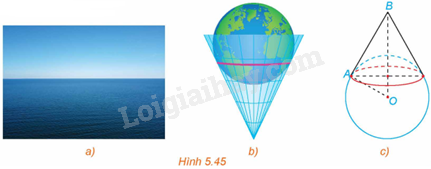
Nếu đứng trước biển và nhìn ra xa, người ta sẽ thấy một đường giao giữa mặt biển và bầu trời, đó là đường chân trời đối với người quan sát (H.5.45a). Về mặt Vật lí, đường chân trời là đường giới hạn phần Trái Đất mà người quan sát có thể nhìn thấy được (phần còn lại bị chính Trái Đất che khuất). Ta có thể hình dung rằng, nếu người quan sát ở tại đỉnh một chiếc nón và Trái Đất được “thả” vào trong chiếc nón đó, thì đường chân trời trong trường hợp này là đường chạm giữa Trái Đất và chiếc nón (H.5.45b). Trong mô hình toán học, đường chân trời đối với người quan sát tại vị trí B là tập hợp những điểm A nằm trên bề mặt Trái Đất sao cho \(\widehat {BAO} = {90^o}\), với O là tâm Trái Đất (H.5.45c). Trong không gian Oxyz, giả sử bề mặt Trái Đất (S) có phương trình \({x^2} + {y^2} + {z^2} = 1\) và người quan sát ở vị trí \(B\left( {1;1; - 1} \right)\).
Gọi A là một vị trí bất kì trên đường chân trời đối với người quan sát ở vị trí B. Tính khoảng cách AB.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về phương trình mặt cầu để xác định ví trị của điểm so với mặt cầu: Cho mặt cầu (S) tâm I, bán kính R và điểm M bất kì trong không gian:
+ Nếu \(IM = R\) thì M nằm trên mặt cầu (S) tâm I.
+ Nếu \(IM > R\) thì M nằm ngoài mặt cầu (S) tâm I.
+ Nếu \(IM < R\) thì M nằm trong mặt cầu (S) tâm I.
Lời giải chi tiết
Bề mặt Trái Đất (S) có tâm \(O\left( {0;0;0} \right)\) và bán kính \(R = 1\).
Vì A nằm trên bề mặt Trái Đất nên \(AO = R = 1\).
\(B{O^2} = {\left( {1 - 0} \right)^2} + {\left( {1 - 0} \right)^2} + {\left( { - 1 - 0} \right)^2} = 3\).
Vì tam giác BAO vuông tại A nên theo định lí Pythagore ta có:
\(A{B^2} = B{O^2} - A{O^2} = 3 - {1^2} = 2 \Rightarrow AB = \sqrt 2 \).
Vậy khoảng cách AB là \(\sqrt 2 \).
- Giải bài tập 5.51 trang 63 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải bài tập 5.50 trang 63 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải bài tập 5.49 trang 63 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải bài tập 5.48 trang 63 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải bài tập 5.47 trang 63 SGK Toán 12 tập 2 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 54 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 41 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 29 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 12 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 4 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 54 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 41 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 29 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 12 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 4 SGK Toán 12 tập 2 - Kết nối tri thức











Danh sách bình luận