Giải bài tập 4 trang 104 SGK Toán 9 tập 1 - Cánh diều

Cho bốn điểm (O,M,N,P) cùng nằm trên một đường thẳng sao cho điểm (M) nằm giữa hai điểm (O) và (N); điểm (N) nằm giữa hai điểm (M) và (P). Gọi (a,b,c) lần lượt là các đường thẳng đi qua (M,N,P) và vuông góc với đường thẳng (OP). Xác định vị trí tương đối của mỗi đường thẳng (a,b,c) và đường tròn (left( {O;ON} right)).

Đề bài

Cho bốn điểm \(O,M,N,P\) cùng nằm trên một đường thẳng sao cho điểm \(M\) nằm giữa hai điểm \(O\) và \(N\); điểm \(N\) nằm giữa hai điểm \(M\) và \(P\). Gọi \(a,b,c\) lần lượt là các đường thẳng đi qua \(M,N,P\) và vuông góc với đường thẳng \(OP\). Xác định vị trí tương đối của mỗi đường thẳng \(a,b,c\) và đường tròn \(\left( {O;ON} \right)\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Vẽ hình, dựa vào hình ảnh trực quan để xác định.

Lời giải chi tiết

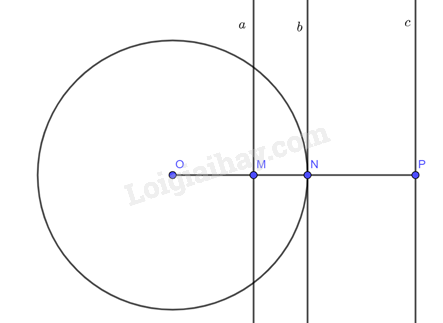
- Đường thẳng \(a\) và đường tròn \(\left( {O;ON} \right)\) cắt nhau.

- Đường thẳng \(b\) và đường tròn \(\left( {O;ON} \right)\) tiếp xúc nhau.

- Đường thẳng \(c\) và đường tròn \(\left( {O;ON} \right)\) không giao nhau.

Bình luận

Chia sẻ

Bình chọn:

3.9 trên 7 phiếu

Bài tiếp theo

Giải bài tập 5 trang 105 SGK Toán 9 tập 1 - Cánh diều
Cho điểm (O) và đường thẳng (a) không đi qua (O). a) Vẽ điểm (H) là hình chiếu của điểm (O) trên đường thẳng (a). b) Từ đó, vẽ ba đường tròn tâm (O) lần lượt: không giao với đường thẳng (a;) tiếp xúc với đường thẳng (a;) cắt đường thẳng (a) tại hai điểm phân biệt.
Giải bài tập 3 trang 104 SGK Toán 9 tập 1 - Cánh diều
Trên mặt phẳng, một vật nhỏ chuyển động trên đường tròn tâm (O) bán kính 2m, một vật nhỏ khác chuyển động trên đường thẳng (a) bằng 3m. Hai vật nhỏ có bao giờ gặp nhau không?
Giải bài tập 2 trang 104 SGK Toán 9 tập 1 - Cánh diều
Trong Hình 30, mép ngoài cửa ra vào có dạng một phần của đường tròn bán kính 1,6m. Hãy tính chiều cao (HK) của cửa đó, biết (AH = 0,9m).
Giải bài tập 1 trang 104 SGK Toán 9 tập 1 - Cánh diều
Đồng hồ treo tường trang trí ở Hình 29 gợi nên vị trí tương đối của đường thẳng và đường tròn. Quan sát Hình 29 và chỉ ra hình ảnh đường thẳng và đường tròn: a) Cắt nhau; b) Tiếp xúc nhau; c) Không giao nhau.
Giải mục 3 trang 103, 104 SGK Toán 9 tập 1 - Cánh diều
Trong Hình 25, cột thẳng đứng và biển quảng cáo có dạng hình tròn gợi nên hình ảnh của đường thẳng và đường tròn không giao nhau. Theo em, đường thẳng và đường tròn không giao nhau thì chúng có điểm chung hay không?
Giải mục 2 trang 102 SGK Toán 9 tập 1 - Cánh diều
Trong bức ảnh ở Hình 22, sợi dây dưới cùng và bánh xe gợi nên hình ảnh đường thẳng và đường tròn tiếp xúc nhau. Theo em, đường thẳng và đường tròn đó có bao nhiêu điểm chung?
Giải mục 1 trang 101, 102 SGK Toán 9 tập 1 - Cánh diều
Trong bức ảnh ở Hình 22, sợi dây dưới cùng và bánh xe gợi nên hình ảnh đường thẳng và đường tròn tiếp xúc nhau. Theo em, đường thẳng và đường tròn đó có bao nhiêu điểm chung?
Lý thuyết Vị trí tương đối của đường thẳng và đường tròn Toán 9 Cánh diều
1. Đường thẳng và đường tròn cắt nhau Khi đường thẳng và đường tròn có hai điểm chung thì ta nói đường thẳng và đường tròn cắt nhau. Nếu đường thẳng và đường tròn cắt nhau thì mỗi điểm chung được gọi là một giao điểm.