Giải bài tập 3 trang 117 SGK Toán 9 tập 1 - Cánh diều

Trong Hình 63, cho biết (AB = OA). a) Tính số đo góc (AOB). b) Tính số đo cung nhỏ (AB) và cung lớn (AB) của (left( O right)). c) Tính số đo góc (MIN). d) Tính số đo cung nhỏ (MN) và cung lớn (MN) của (left( I right)). e) Tính số đo góc (MKN).

Tổng hợp đề thi giữa kì 2 lớp 9 tất cả các môn - Cánh diều

Toán - Văn - Anh - KHTN

Đề bài

Trong Hình 63, cho biết $AB = OA$ .

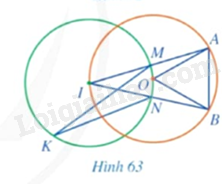
a) Tính số đo góc $AOB$ .

b) Tính số đo cung nhỏ $AB$ và cung lớn $AB$ của $\left( O \right)$ .

c) Tính số đo góc $MIN$ .

d) Tính số đo cung nhỏ $MN$ và cung lớn $MN$ của $\left( I \right)$ .

e) Tính số đo góc $MKN$ .

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Dựa vào tính chất số đo góc ở tâm và số đo góc nội tiếp để chứng minh.

Lời giải chi tiết

a) Xét tam giác $OAB$ có: $OA = OB = AB = R$ nên tam giác $OAB$ đều.

Vậy $\widehat {AOB} = 60^\circ$ .

b) Xét đường tròn $\left( O \right)$ có:

+ $\widehat {AOB}$ là góc ở tâm chắn cung $AB$ nên $\widehat{AOB}=sđ\overset\frown{AB}=60{}^\circ$

+ $sđ\overset\frown{A{{B}_{lớn}}}=360{}^\circ -sđ\overset\frown{A{{B}_{nhỏ}}}=360{}^\circ -60{}^\circ =300{}^\circ$

c) Xét đường tròn $\left( O \right)$ có:

+ $\widehat {MIN}$ là góc nội tiếp chắn cung $AB$ nên $\widehat{MIN}=\frac{1}{2}sđ\overset\frown{AB}=30{}^\circ$

d) Xét đường tròn $\left( I \right)$ có:

+ $\widehat {MIN}$ là góc ở tâm chắn cung $MN$ nên $\widehat{MIN}=sđ\overset\frown{MN}=30{}^\circ$

+ $sđ\overset\frown{M{{N}_{lớn}}}=360{}^\circ -sđ\overset\frown{M{{N}_{nhỏ}}}=360{}^\circ -30{}^\circ =330{}^\circ$

e) Xét đường tròn $\left( I \right)$ có:

+ $\widehat {MKN}$ là góc nội tiếp chắn cung $MN$ nên $\widehat{MKN}=\frac{1}{2}sđ\overset\frown{MN}=15{}^\circ$

Bình luận

Chia sẻ

Bình chọn:

3.9 trên 7 phiếu

Bài tiếp theo

Giải bài tập 4 trang 117 SGK Toán 9 tập 1 - Cánh diều
Biểu đồ hình quạt tròn ở Hình 64 mô tả các thành phần của một chai nước ép hoa quả (tính theo tỉ số phần trăm). Hãy cho biết các cung tương ứng với phần biểu diễn thành phần việt quất, táo, mật ong lần lượt có số đo là bao nhiêu độ.
Giải bài tập 5 trang 117 SGK Toán 9 tập 1 - Cánh diều
Cho hai đường tròn (left( O right),left( I right)) cắt nhau tại hai điểm (A,B). Kẻ các đoạn thẳng (AC,AD) lần lượt là đường kính của hai đường tròn (left( O right),left( I right)). Chứng minh ba điểm (B,C,D) thẳng hàng.
Giải bài tập 6 trang 117 SGK Toán 9 tập 1 - Cánh diều
Hãy sử dụng compa và thước thẳng để vẽ tam giác (ABC) vuông tại (A) và giải thích kết quả.
Giải bài tập 2 trang 117 SGK Toán 9 tập 1 - Cánh diều
Cho đường tròn (left( {O;R} right)) và dây (AB) sao cho (widehat {AOB} = 90^circ ). Giả sử (M,N) lần lượt là các điểm thuộc cung lớn (AB) và cung nhỏ (AB) ((M,N) khác (A) và (B)). a) Tính độ dài đoạn thẳng (AB) theo (R). b) Tính số đo các góc (ANB) và (AMB).
Giải bài tập 1 trang 117 SGK Toán 9 tập 1 - Cánh diều
Quan sát Hình 62, hãy cho biết: a) 6 góc ở tâm có hai cạnh lần lượt chứa hai trong bốn điểm (A,B,C,D); b) 4 góc nội tiếp có hai cạnh lần lượt chứa ba điểm trong bốn điểm.
Giải mục 3 trang 115, 116 SGK Toán 9 tập 1 - Cánh diều
Trong Hình 55, đỉnh của góc (AIB) có thuộc đường tròn hay không? Hai cạnh của góc chứa hai dây cung nào của đường tròn?
Giải mục 2 trang 112, 113, 114 SGK Toán 9 tập 1 - Cánh diều
Quan sát góc ở tâm (AOB) (khác góc bẹt) ở Hình 48, cho biết trong hai phần đường tròn được tô màu xanh và màu đỏ, phần nào nằm bên trong, phần nào nằm bên ngoài góc (AOB).
Giải mục 1 trang 111 SGK Toán 9 tập 1 - Cánh diều
Cho đường tròn (left( O right)). Hãy vẽ góc (xOy) có đỉnh là tâm (O) của đường tròn đó.
Lý thuyết Góc ở tâm, góc nội tiếp Toán 9 Cánh diều
1. Góc ở tâm Định nghĩa Góc ở tâm là góc có đỉnh trùng với tâm đường tròn.

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Cánh diều - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com

>> Chi tiết khoá học xem: TẠI ĐÂY

Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.