Giải bài tập 2 trang 79 SGK Toán 9 tập 2 - Cánh diều

Cho đường tròn (I) nội tiếp tam giác ABC và lần lượt tiếp xúc với các cạnh BC, CA, AB tại M, N, P. Chứng minh (widehat {AIN} = widehat {PMN} = frac{1}{2}widehat {PIN.})

Đề bài

Cho đường tròn (I) nội tiếp tam giác ABC và lần lượt tiếp xúc với các cạnh BC, CA, AB tại M, N, P. Chứng minh \(\widehat {AIN} = \widehat {PMN} = \frac{1}{2}\widehat {PIN.}\)

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Bước 1: Lý thuyết: Góc ở tâm bằng số đo cung bị chắn, góc nội tiếp bằng một nửa số đo cung bị chắn, suy ra \(\widehat {PMN} = \frac{1}{2}\widehat {PIN.}\)

Bước 2: Sử dụng tính chất 2 tiếp tuyến cắt nhau để suy ra \(\widehat {AIN} = \frac{1}{2}\widehat {PIN.}\)

Lời giải chi tiết

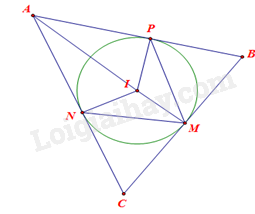
Xét (I) có:

\(\widehat {PIN}\) là góc ở tâm chắc cung NP nên \(\widehat {PIN}\)= sđ\(\overset\frown{NP}\).

\(\widehat {PMN}\) là góc nội tiếp chắc cung NP nên \(\widehat {PMN}\) = \(\frac{1}{2}\)sđ\(\overset\frown{NP}\).

Suy ra \(\widehat {PMN} = \frac{1}{2}\widehat {PIN.}\)(1)

Ta lại có: \(IN \bot AC,IP \bot AB\) nên AB, AC là 2 tiếp tuyến của (I) nên IA là tia phân giác của góc PIN, hay \(\widehat {AIN} = \frac{1}{2}\widehat {PIN.}\)(2)

Từ (1) và (2) ta có \(\widehat {AIN} = \widehat {PMN} = \frac{1}{2}\widehat {PIN.}\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài tập 3 trang 79 SGK Toán 9 tập 2 - Cánh diều
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Các đường cao AK, BM cắt nhau tại trực tâm H của tam giác ABC. Tia AK cắt đường tròn (O) tại điểm N (khác A). Chứng minh: a)(widehat {CBM} = widehat {CAK}) b) Tam giác BHN cân. c) BC là đường trung trực của HN.
Giải bài tập 4 trang 79 SGK Toán 9 tập 2 - Cánh diều
Cho tứ giác nội tiếp ABCD có hai tia CD và BA cắt nhau tại I. Chứng minh: a)(widehat {IAD} = widehat {BCD}.) b) IA.IB = ID.IC.
Giải bài tập 5 trang 79 SGK Toán 9 tập 2 - Cánh diều
Cho tứ giác ABCD và các điểm M, N lần lượt thuộc các đoạn thẳng AB và CD sao cho các tứ giác AMND, BMNC là các tứ giác nội tiếp. Chứng minh (widehat A + widehat B = 180^circ .)
Giải bài tập 6 trang 79 SGK Toán 9 tập 2 - Cánh diều
Khung thép của một phần sân khấu có dạng đường tròn bán kính 15m. Mắt của một người thợ ở vị trí A nhìn hai đèn ở các vị trí B, C (A, B, C cùng thuộc đường tròn bán kính 15m), bằng cách nào đó, người thợ thấy rằng góc nhìn (widehat {BAC} = 30^circ ) (hình 31). Khoảng cách giữa hai vị trí B và C bằng bao nhiêu mét?
Giải bài tập 1 trang 79 SGK Toán 9 tập 2 - Cánh diều
Cho tứ giác ABCD nội tiếp đường tròn có (widehat C = 80^circ .) Số đo góc A là: A. (80^circ ) B. (160^circ ) C. (40^circ ) D. (100^circ )