 SBT Toán 9 - giải SBT Toán 9 - Chân trời sáng tạo
SBT Toán 9 - giải SBT Toán 9 - Chân trời sáng tạo
 Bài 4. Biến đổi đơn giản biểu thức chứa căn thức bậc ha..
Bài 4. Biến đổi đơn giản biểu thức chứa căn thức bậc ha..
Giải bài 8 trang 51 sách bài tập toán 9 - Chân trời sáng tạo tập 1
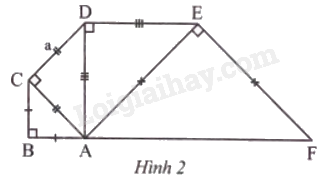
Một phần khung của một cây cầu gồm các thanh thép tạo thành các tam giác vuông cân như Hình 2. Biết rằng cạnh CD có độ dài a (m). Tính độ dài của đoạn BF theo a.
Đề bài
Một phần khung của một cây cầu gồm các thanh thép tạo thành các tam giác vuông cân như Hình 2. Biết rằng cạnh CD có độ dài a (m). Tính độ dài của đoạn BF theo a.
Phương pháp giải - Xem chi tiết
Dựa vào: Định lý Pytago để tính AD, AE và AF.
Từ đó: tính BF = AB + AF.
Lời giải chi tiết
Ta có:
AD = \(\sqrt {A{C^2} + C{D^2}} = \sqrt {2C{D^2}} = CD\sqrt 2 = a\sqrt 2 (m).\)
Tương tự, tính được:
\(AE = AD\sqrt 2 = 2a (m)\);
AF = AE\(\sqrt 2 = 2a\sqrt 2 (m)\)
\(AB = \frac{{AC}}{{\sqrt 2 }} = \frac{a}{{\sqrt 2 }} = \frac{{a\sqrt 2 }}{2}(m)\).
Từ đó, \(BF = AB + AF = \frac{{a\sqrt 2 }}{2} + 2a\sqrt 2 = \frac{{5a\sqrt 2 }}{2}(m)\).
- Giải bài 9 trang 51 sách bài tập toán 9 - Chân trời sáng tạo tập 1
- Giải bài 10 trang 51 sách bài tập toán 9 - Chân trời sáng tạo tập 1
- Giải bài 11 trang 51 sách bài tập toán 9 - Chân trời sáng tạo tập 1
- Giải bài 7 trang 51 sách bài tập toán 9 - Chân trời sáng tạo tập 1
- Giải bài 6 trang 51 sách bài tập toán 9 - Chân trời sáng tạo tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải bài 4 trang 86 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 1 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 16 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 15 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 14 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 16 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 15 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 14 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 13 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 12 trang 108 sách bài tập toán 9 - Chân trời sáng tạo tập 2












Danh sách bình luận