Giải bài 65 trang 84 sách bài tập toán 8 – Cánh diều
Cho tam giác \(ABC\), điểm \(M\) thuộc cạnh \(BC\) sao cho \(MC=2MB\). Đường thẳng qua \(M\) song song với \(AC\) cắt \(AB\) ở \(D\).
Tổng hợp đề thi giữa kì 2 lớp 8 tất cả các môn - Cánh diều
Toán - Văn - Anh - Khoa học tự nhiên
Đề bài
Cho tam giác \(ABC\), điểm \(M\) thuộc cạnh \(BC\) sao cho \(MC=2MB\). Đường thẳng qua \(M\) song song với \(AC\) cắt \(AB\) ở \(D\). Đường thẳng qua \(M\) song song với \(AB\) cắt \(AC\) ở \(E\). Gọi \(x,y\) lần lượt là chu vi tam giác \(DBM\) và tam giác \(ECM\). Tính \(x+2y\), biết chu vi tam giác \(ABC\) bằng 30 cm.
Phương pháp giải - Xem chi tiết
Dựa vào trường hợp đồng dạng thứ nhất: cạnh – cạnh – cạnh
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
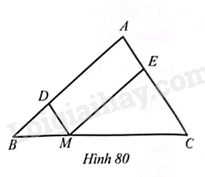
Ta có \(\Delta BDM\backsim \Delta BAC\)
\(=>\frac{BD}{AB}=\frac{BM}{BC}=\frac{DM}{AC}=\frac{BD+BM+DM}{AB+BC+CA}=\frac{1}{3}\)
→ Chu vi tam giác \(DBM\) bằng một phần ba chu vi tam giác \(ABC\). Vì thế chu vi tam giác \(DMB\) bằng 10 cm. tương tự, chu vi tam giác \(ECM\) bằng 20 cm.
→ Vậy \(x+2y=50\) (cm).













Danh sách bình luận