-
Toán 8 tập 1 - Chân trời sáng tạo
-
Toán 8 tập 2 - Chân trời sáng tạo
Giải bài 4 trang 88 SGK Toán 8 tập 1– Chân trời sáng tạo
Cho tam giác
Đề bài
Cho tam giác \(ABC\) vuông tại \(A\), đường trung tuyến \(AM\). Biết \(AB = 8\)cm; \(AC = 15\)cm. Độ dài đoạn \(AM\) là:
A. 8,5cm
B. 8cm
C. 7cm
D. 7,5cm
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng ĐL Pythagore rồi tính độ dài cạnh \(BC\); \(AM\)
Lời giải chi tiết
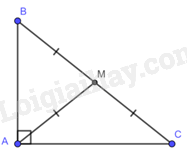
Áp dụng định lí Pythagpre vào \(\Delta ABC\) vuông tại \(A\) ta có:
\(B{C^2} = A{B^2} + A{C^2} = {8^2} + {15^2} = 64 + 225 = 289 = {17^2}\)
\(BC = 17\) cm
Xét \(\Delta ABC\) có \(AM\) là trung tuyến nên bằng nửa cạnh huyền \(BC\)
Suy ra \(AM = \frac{1}{2}BC = \frac{1}{2}.17 = 8.5\) cm
Bình luận
Chia sẻ
- Giải bài 5 trang 88 SGK Toán 8 tập 1– Chân trời sáng tạo
- Giải bài 6 trang 88 SGK Toán 8 tập 1– Chân trời sáng tạo
- Giải bài 7 trang 88 SGK Toán 8 tập 1– Chân trời sáng tạo
- Giải bài 8 trang 89 SGK Toán 8 tập 1– Chân trời sáng tạo
- Giải bài 9 trang 89 SGK Toán 8 tập 1– Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Chân trời sáng tạo - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
- Lý thuyết Xác suất lí thuyết và xác suất thực nghiệm SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Mô tả xác suất bằng tỉ số SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Hai hình đồng dạng SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Xác suất lí thuyết và xác suất thực nghiệm SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Mô tả xác suất bằng tỉ số SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Hai hình đồng dạng SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác SGK Toán 8 - Chân trời sáng tạo
