-
SBT TOÁN TẬP 1 - CÁNH DIỀU
-
SBT TOÁN TẬP 2 - CÁNH DIỀU
SBT Toán 11 - giải SBT Toán 11 - Cánh diều
Bài 3. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện ..
Giải bài 31 trang 100 sách bài tập toán 11 - Cánh diều
Cho hình chóp \(S.ABCD\). Gọi \({\alpha _1}\), \({\alpha _2}\), \({\alpha _3}\)
Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Cánh diều
Toán - Văn - Anh - Lí - Hóa - Sinh
Đề bài
Cho hình chóp \(S.ABCD\). Gọi \({\alpha _1}\), \({\alpha _2}\), \({\alpha _3}\), \({\alpha _4}\) lần lượt là góc giữa các đường thẳng \(SA\), \(SB\), \(SC\), \(SD\) và mặt phẳng \(\left( {ABCD} \right)\). Chứng minh rằng \(SA = SB = SC = SD \Leftrightarrow {\alpha _1} = {\alpha _2} = {\alpha _3} = {\alpha _4}\).
Phương pháp giải - Xem chi tiết
Gọi \(H\) là hình chiếu của \(S\) trên \(\left( {ABCD} \right)\). Chỉ ra rằng \({\alpha _1} = \widehat {SAH}\), \({\alpha _2} = \widehat {SBH}\), \({\alpha _3} = \widehat {SCH}\), \({\alpha _4} = \widehat {SDH}\), rồi suy ra điều phải chứng minh.
Lời giải chi tiết
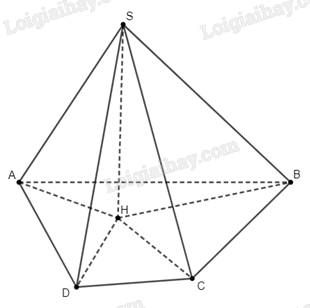
Gọi \(H\) là hình chiếu của \(S\) trên \(\left( {ABCD} \right)\).
Dễ thấy rằng \({\alpha _1}\), \({\alpha _2}\), \({\alpha _3}\), \({\alpha _4}\) là những góc tạo bởi đường thẳng và mặt phẳng, nên chúng không lớn hơn \({90^o}\).
Vì \(H\) là hình chiếu của \(S\) trên \(\left( {ABCD} \right)\), ta suy ra \({\alpha _1} = \widehat {SAH}\).
Tam giác \(SAH\) vuông tại \(H\), ta có \(\sin {\alpha _1} = \sin \widehat {SAH} = \frac{{SH}}{{SA}}\).
Chứng minh tương tự, ta cũng có:
+ \({\alpha _2} = \widehat {SBH}\), \(\sin {\alpha _2} = \sin \widehat {SBH} = \frac{{SH}}{{SB}}\),
+ \({\alpha _3} = \widehat {SCH}\), \(\sin {\alpha _3} = \sin \widehat {SCH} = \frac{{SH}}{{SC}}\),
+ \({\alpha _4} = \widehat {SDH}\), \(\sin {\alpha _4} = \sin \widehat {SDH} = \frac{{SH}}{{SD}}\),
Vậy, \(SA = SB = SC = SD \Leftrightarrow \frac{{SH}}{{SA}} = \frac{{SH}}{{SB}} = \frac{{SH}}{{SC}} = \frac{{SH}}{{SD}}\)
\( \Leftrightarrow \sin {\alpha _1} = \sin {\alpha _2} = \sin {\alpha _3} = \sin {\alpha _4} \Leftrightarrow {\alpha _1} = {\alpha _2} = {\alpha _3} = {\alpha _4}\).
Bài toán được chứng minh.
Bình luận
Chia sẻ
- Giải bài 32 trang 100 sách bài tập toán 11 - Cánh diều
- Giải bài 30 trang 100 sách bài tập toán 11 - Cánh diều
- Giải bài 29 trang 100 sách bài tập toán 11 - Cánh diều
- Giải bài 28 trang 100 sách bài tập toán 11 - Cánh diều
- Giải bài 27 trang 99 sách bài tập toán 11 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
