Giải bài 2 trang 61 sách bài tập toán 11 - Chân trời sáng tạo tập 2

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a. Cho biết \(SA = a\) và \(SA \bot \left( {ABCD} \right)\).

Đề bài

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a. Cho biết \(SA = a\) và \(SA \bot \left( {ABCD} \right)\). Trên BC lấy điểm I sao cho tam giác SDI vuông tại S. Biết góc giữa hai mặt phẳng (SDI) và (ABCD) là \({60^0}\). Tính độ dài SI.

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng.

Lời giải chi tiết

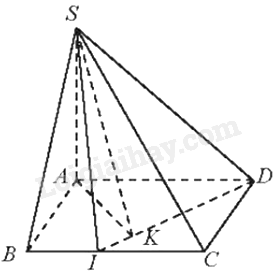
Kẻ \(AK \bot ID\) tại K. Vì \(SA \bot \left( {ABCD} \right),AK \subset \left( {ABCD} \right) \Rightarrow SA \bot ID\), mà \(AK \bot ID\) nên \(ID \bot \left( {SAK} \right) \Rightarrow ID \bot SK\)

Ta có: \(AK \bot ID,ID \bot SK,AK \subset \left( {ABCD} \right),SK \subset \left( {SID} \right)\), ID là giao tuyến của hai mặt phẳng SID và ABCD. Do đó, \(\left( {\left( {SID} \right),\left( {ABCD} \right)} \right) = \left( {SK,AK} \right) = \widehat {SKA} = {60^0}\)

Vì \(SA \bot \left( {ABCD} \right),AD,AK \subset \left( {ABCD} \right) \Rightarrow SA \bot AD,SA \bot AK\)

Áp dụng định lí Pythagore vào tam giác SAD vuông tại A có:

\(SD = \sqrt {S{A^2} + A{D^2}} = \sqrt {{a^2} + {{\left( {2a} \right)}^2}} = a\sqrt 5 \)

Tam giác SAK vuông tại A nên: \(\sin \widehat {SKA} = \frac{{SA}}{{SK}} \Rightarrow SK = \frac{{SA}}{{\sin \widehat {SKA}}} = \frac{{2a\sqrt 3 }}{3}\)

Tam giác SID vuông tại S, đường cao SK có:

\(\frac{1}{{S{I^2}}} + \frac{1}{{S{D^2}}} = \frac{1}{{S{K^2}}} \) \( \Rightarrow \frac{1}{{S{I^2}}} = \frac{1}{{S{K^2}}} - \frac{1}{{S{D^2}}} = \left( {\frac{9}{{12{a^2}}}} \right) - \frac{1}{{{{\left( {a\sqrt 5 } \right)}^2}}} = \frac{{11}}{{20{a^2}}} \) \( \Rightarrow SI = \frac{{2a\sqrt {55} }}{{11}}\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 3 trang 61 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và \(SA \bot \left( {ABC} \right)\).
Giải bài 4 trang 61 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD).
Giải bài 5 trang 62 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(SA = a\sqrt 3 \). Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy.
Giải bài 6 trang 62 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Người ta cần sơn tất cả các mặt của một khối bê tông hình chóp cụt tứ giác đều, đáy lớn có cạnh bằng 2m, đáy nhỏ có cạnh bằng 1m và cạnh bên bằng 2m (Hình 14). Tính tổng diện tích các bề mặt cần sơn.
Giải bài 7 trang 62 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Một hộp đèn treo trần có hình dạng lăng trụ đứng lục giác đều (Hình 15), cạnh đáy bằng 10cm và cạnh bên bằng 50cm. Tính tỉ số giữa diện tích xung quanh và diện tích một mặt đáy của hộp đèn.
Giải bài 1 trang 61 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho tứ diện ABCD có tam giác BCD vuông cân tại B và \(AB \bot \left( {BCD} \right)\). Cho biết \(BC = a\sqrt 2 ,AB = \frac{a}{{\sqrt 3 }}\).