Giải bài 19 trang 108 sách bài tập toán 9 - Cánh diều tập 1
Cho đường tròn tâm O bán kính 15cm. Điểm A nằm ngoài đường tròn sao cho \(OA = 25\)cm. Kẻ tiếp tuyến AB của đường tròn (O). Kẻ dây BC vuông góc với OA tại H. a) Chứng minh AC là tiếp tuyến của đường tròn (O). b) Tính độ dài các cạnh của tam giác ABC.
Đề bài
Cho đường tròn tâm O bán kính 15cm. Điểm A nằm ngoài đường tròn sao cho \(OA = 25\)cm. Kẻ tiếp tuyến AB của đường tròn (O). Kẻ dây BC vuông góc với OA tại H.
a) Chứng minh AC là tiếp tuyến của đường tròn (O).
b) Tính độ dài các cạnh của tam giác ABC.
Phương pháp giải - Xem chi tiết
a) Chứng minh \(\Delta OAC = \Delta OAB\left( {g.c.g} \right)\) để suy ra \(\widehat {ACO} = 90^\circ \).
b) Tính AC: định lý Pythagore trong tam giác vuông AOC.
Tính CB: \(CB = HC + HB.\)
Lời giải chi tiết
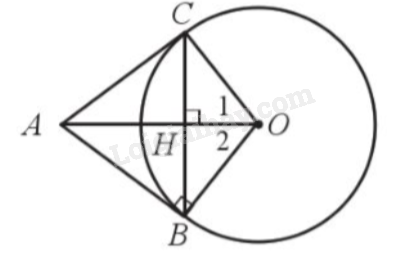
a) Tam giác OCB có \(OC = OB\left( { = R} \right)\) nên tam giác OCB cân tại O, mà \(OH \bot CB\) nên OH là đường cao đồng thời là đường phân giác của tam giác OCB, suy ra \(\widehat {{O_1}} = \widehat {{O_2}}\).
Xét tam giác OAC và OAB có:
\(\widehat {{O_1}} = \widehat {{O_2}}\);
OA chung;
\(OC = OB\)
Do đó \(\Delta OAC = \Delta OAB\left( {g.c.g} \right)\), suy ra \(\widehat {ACO} = \widehat {ABO}\).
Mà \(\widehat {ABO} = 90^\circ \)(do AB là tiếp tuyến của đường tròn (O)) nên \(\widehat {ACO} = 90^\circ \).
Vậy AC là tiếp tuyến của (O).
b) Áp dụng định lý Pythagore trong tam giác vuông AOC ta có:
\(AC = \sqrt {A{O^2} - C{O^2}} = \sqrt {{{25}^2} - {{15}^2}} = 20\)cm.
Vì \(\Delta OAC = \Delta OAB\) nên \(AC = AB = 20\)cm.
Xét tam giác OCH và OAC ta có:
\(\widehat {{O_1}}\) chung;
\(\widehat {OHC} = \widehat {OCA}\left( { = 90^\circ } \right)\)
nên \(\Delta OHC\backsim \Delta OCA\left( g.g \right)\)
Do đó \(\frac{{HC}}{{CA}} = \frac{{OC}}{{OA}}\) hay \(HC = \frac{{CA.OC}}{{OA}} = \frac{{20.15}}{{25}} = 12\)cm.
Vì OH là đường trung tuyến của tam giác OCB nên \(HC = HB = 12cm\)
và \(CB = HC + HB = 12 + 12 = 24cm\).
Vậy \(AC = AB = 20\)cm; \(CB = 24cm\).
Bình luận
Chia sẻ
- Giải bài 20 trang 109 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 21 trang 109 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 22 trang 109 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 23 trang 109 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 24 trang 109 sách bài tập toán 9 - Cánh diều tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Cánh diều - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
Các bài khác cùng chuyên mục
