-
Toán 8 tập 1 - Chân trời sáng tạo
-
Toán 8 tập 2 - Chân trời sáng tạo
Giải Bài 15 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo
Một người đi bộ với tốc độ không đổi 3(km/h). Gọi (sleft( {km} right)) là quãng đường đi được trong (t) (giờ). a) Lập công thức tính (s) theo (t). b) Vẽ đồ thị của hàm số (s) theo biến số (t).
Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - Khoa học tự nhiên
Đề bài
Một người đi bộ với tốc độ không đổi 3\(km/h\). Gọi \(s\left( {km} \right)\) là quãng đường đi được trong \(t\) (giờ).
a) Lập công thức tính \(s\) theo \(t\).
b) Vẽ đồ thị của hàm số \(s\) theo biến số \(t\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Công thức tính quãng đường theo vận tốc và thời gian là:
\(s = v.t\) với \(s\) là quãng đường; \(v\) là vận tốc và \(t\) là thời gian.
Để vẽ đồ thị hàm số \(y = ax\), ta thường thực hiện các bước sau:
Bước 1: Xác định một điểm \(M\) trên đồ thị khác gốc tọa độ \(O\), chẳng hạn \(M\left( {1;a} \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(O\) và \(M\).
Lời giải chi tiết
a) Quãng được vật đi được với vận tốc 3 \(km/h\)trong khoảng thời gian \(t\) (giờ) là:
\(s = v.t = 3.t\).
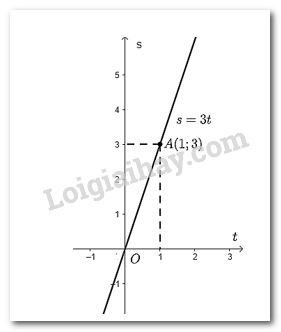
b) Vẽ đồ thị hàm số \(s = 3.t\)
Cho \(t = 1 \Rightarrow s = 3.1 = 3\)\( \Rightarrow \) đồ thị hàm số đi qua điểm \(M\left( {1;3} \right)\).
Đồ thị hàm số \(s = 3.t\) là đường thẳng đi qua hai điểm \(O\) và \(M\).
Bình luận
Chia sẻ
- Giải Bài 16 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo
- Giải Bài 17 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo
- Giải Bài 18 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo
- Giải Bài 19 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo
- Giải Bài 14 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Chân trời sáng tạo - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
- Lý thuyết Xác suất lí thuyết và xác suất thực nghiệm SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Mô tả xác suất bằng tỉ số SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Hai hình đồng dạng SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Xác suất lí thuyết và xác suất thực nghiệm SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Mô tả xác suất bằng tỉ số SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Hai hình đồng dạng SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác SGK Toán 8 - Chân trời sáng tạo
