Giải bài 15 trang 106 sách bài tập toán 9 - Cánh diều tập 1

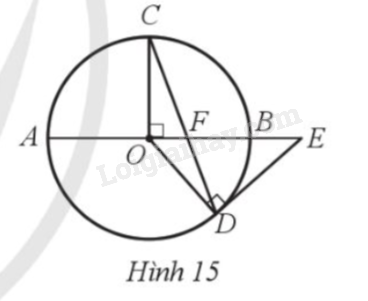
Cho đường tròn tâm O đường kính AB = 2R, bán kính OC vuông góc với AB tại O. Lấy điểm F thuộc đoạn thẳng OB, tia CF cắt đường tròn (O) tại D. Tiếp tuyến tại D của đường tròn (O) cắt AB tại E (hình 15). Chứng minh EF = ED.

Đề bài

Cho đường tròn tâm O đường kính AB = 2R, bán kính OC vuông góc với AB tại O. Lấy điểm F thuộc đoạn thẳng OB, tia CF cắt đường tròn (O) tại D. Tiếp tuyến tại D của đường tròn (O) cắt AB tại E (hình 15). Chứng minh EF = ED.

Phương pháp giải - Xem chi tiết

Để chứng minh \(EF = ED\) ta chứng minh như sau:

\(\widehat C + \widehat {OFC} = 90^\circ \),\(\widehat {ODF} + \widehat {FDE} = 90^\circ \) suy ra \(\widehat {FDE} = \widehat {DFE}\) (cùng bằng \(\widehat {OFC}\))

Do đó \(\Delta DEF\) cân tại E suy ra \(EF = ED\)

Lời giải chi tiết

Do DE là tiếp tuyến của (O) nên \(OD \bot DE\) hay \(\widehat {ODE} = 90^\circ \).

Xét tam giác OCD có \(OC = OD( = R)\) nên tam giác OCD cân tại O, do đó \(\widehat C = \widehat {ODF}\).

Ta lại có \(\widehat C + \widehat {OFC} = 90^\circ \)(tam giác OCF vuông tại O), \(\widehat {ODF} + \widehat {FDE} = \widehat {ODE} = 90^\circ \)

Suy ra \(\widehat {OFC} = \widehat {FDE}\), mà \(\widehat {OFC} = \widehat {DFE}\) (đối đỉnh) nên \(\widehat {FDE} = \widehat {DFE}\).

Xét tam giác DFE có \(\widehat {FDE} = \widehat {DFE}\) nên tam giác DFE cân tại E, do đó EF = ED.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 16 trang 106 sách bài tập toán 9 - Cánh diều tập 1
Cho hình vuông ABCD. Trên đường chéo BD, lấy điểm H sao cho BH = AB. Qua điểm H kẻ đường thẳng vuông góc với BD cắt AD tại O. a) So sánh OA, OH, HD. b) Xác định vị trí tương đối của BD và đường tròn (O; OA).
Giải bài 17 trang 106 sách bài tập toán 9 - Cánh diều tập 1
Từ điểm A ở ngoài đường tròn (O) vẽ tiếp tuyến AB của đường tròn với B là tiếp điểm. Lấy các điểm C, D thuộc đường tròn (O) sao cho C nằm giữa A và D, O không thuộc AD. Gọi I là trung điểm của đoạn thẳng CD, tia OI cắt AB tại E (Hình 16). Chứng minh: a) \(EB.EA = EI.EO\) b) \(A{B^2} = AC.AD\)
Giải bài 18 trang 107 sách bài tập toán 9 - Cánh diều tập 1
Cho đường tròn (O; 4 cm) và đường thẳng d sao cho khoảng cách từ điểm O đến đường thẳng d là OH = 5 cm. Đường thẳng OH cắt đường tròn (O) tại A. Gọi B là trung điểm của đoạn thẳng OA. Trên đường thẳng d, lấy một điểm I (khác H), kẻ tiếp tuyến IC của đường tròn (O) với C là tiếp điểm (Hình 17). Chứng minh tam giác IBC cân tại I.
Giải bài 14 trang 106 sách bài tập toán 9 - Cánh diều tập 1
Cho đường tròn (O;R) và điểm A sao cho OA = 2R. Kẻ tiếp tuyến AB của đường tròn (O; R) với B là tiếp điểm (hình 14). Tính độ dài đoạn thẳng AB theo R.
Giải bài 13 trang 106 sách bài tập toán 9 - Cánh diều tập 1
Cho hình thang vuông ABCD (\(\widehat A = \widehat D = 90^\circ \)) có AB = 4 cm, BC = 13 cm, CD = 9 cm. a) Tính độ dài đoạn thẳng AD. b) Đường thẳng AD có tiếp xúc với đường tròn đường kính BC hay không? Vì sao?
Giải bài 12 trang 106 sách bài tập toán 9 - Cánh diều tập 1
Cho \(\widehat {xOy} = 30^\circ \) và điểm O’ thuộc tia Oy sao cho OO’ = 4 cm. a) Tính khoảng cách từ điểm O’ đến tia Oy, b) Xác định vị trí tương đối của tia Oy và đường tròn (O’; R) tuỳ theo độ dài R với \(R \le 4\) cm.
Giải bài 11 trang 106 sách bài tập toán 9 - Cánh diều tập 1
Cho đường thẳng a và điểm O với khoảng cách từ điểm O đến đường thẳng a là 1 cm. Vẽ đường tròn tâm O bán kính 3 cm. a) Xác định vị trí tương đối của đường thẳng a và đường tròn (O). b) Gọi A và B là các giao điểm của đường thẳng a và đường tròn (O). Tính độ dài đoạn thẳng AB.