Đề thi học kì 2 Toán 9 - Đề số 2
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đề bài
-
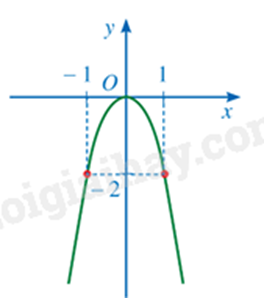
A.
\(2\).
-
B.
\( - 2\).
-
C.
\(\frac{1}{2}\).
-
D.
\(\frac{{ - 1}}{2}\).
Trong các phương trình sau, phương trình nào là phương trình bậc hai một ẩn?
-
A.
\(2x - 4 = 0\).
-
B.
\({x^2} + 2x + 1 = 0\).
-
C.
\({x^2} - \sqrt x + 4 = 0\).
-
D.
\(0{x^2} + 2x - 4 = 0\).
Tìm hai số, biết tổng của chúng bằng 23 và tích của chúng bằng 120. Vậy hai số cần tìm:
-
A.
23 và 120.
-
B.
10 và 8.
-
C.
15 và 8.
-
D.
15 và 18.
Cho bảng tần số tương đối ghép nhóm về thời gian đi từ nhà đến trường của học sinh lớp \(9A\) như sau:
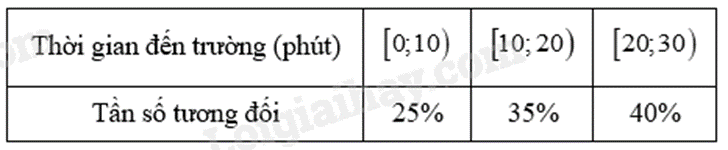
Để vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng, ta dùng giá trị nào đại diện cho nhóm số liệu \(\left[ {20;30} \right)\).
-
A.
\(5\).
-
B.
\(15\).
-
C.
\(25\).
-
D.
\(20\).
Một hộp chứa 4 quả cầu cùng loại trong đó có 1 quả cầu đỏ, 1 quả cầu xanh và 2 quả cầu vàng. Chọn ngẫu nhiên đồng thời ra hai quả cầu. Xác suất của biến cố “Chọn được 1 quả cầu đỏ và 1 quả cầu vàng” là
-
A.
\(\frac{1}{6}\).
-
B.
\(\frac{1}{4}\).
-
C.
\(\frac{1}{3}\).
-
D.
\(\frac{2}{3}\).
Cho tam giác ABC vuông tại A, có \(AB = 24\) cm, \(AC = 18\) cm. Chu vi đường tròn ngoại tiếp tam giác ABC bằng
-
A.
\(30\pi {\rm{cm}}\).
-
B.
\(225\pi {\rm{cm}}\).
-
C.
\(60\pi {\rm{cm}}\).
-
D.
\(15\pi {\rm{cm}}\).
Độ dài bán kính đường tròn ngoại tiếp hình vuông có cạnh bằng 4 cm là:
-
A.
\(3\sqrt 2 cm\).
-
B.
\(4\sqrt 2 cm\).
-
C.
\(\sqrt 2 cm\).
-
D.
\(2\sqrt 2 cm\).
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
Phép quay nào với O là tâm biến tam giác đều thành chính nó?
-
A.
\(90^\circ \).
-
B.
\(100^\circ \).
-
C.
\(110^\circ \).
-
D.
\(120^\circ \).
Cho hình trụ sau. Cạnh AB quét nên mặt xung quanh của hình trụ, mỗi vị trí của cạnh AB gọi là:
-
A.
Đường sinh.
-
B.
Bán kính đáy.
-
C.
Chiều cao.
-
D.
Đường kính đáy.
Cho hình nón có bán kính đáy \(r = 2cm\). Biết diện tích xung quanh của hình nón là \(2\sqrt 5 \pi c{m^3}\), tính thể tích của hình nón.
-
A.
\(\pi c{m^3}\).
-
B.
\(\frac{5}{3}\pi c{m^3}\).
-
C.
\(\frac{4}{3}\pi {\rm{c}}{{\rm{m}}^{\rm{3}}}\).
-
D.
\(\frac{2}{3}\pi {\rm{c}}{{\rm{m}}^{\rm{3}}}\).
-
A.
\(\sqrt {10} cm.\)
-
B.
\(5cm.\)
-
C.
\(10cm.\)
-
D.
\(20cm.\)
Một mảnh vườn hình chữ nhật ABCD có chu vi và diện tích lần lượt là 70 m và 250 \({m^2}\). Người ta chia mảnh vườn đó thành ba khu vực: khu tiểu cảnh ADE, khu trồng hoa BEDF, khu thư giãn BCF với \(BE = DF = 6m\) như mô tả ở hình bên. Gọi chiều dài của mảnh vườn của \(x\left( m \right),x > 0\).
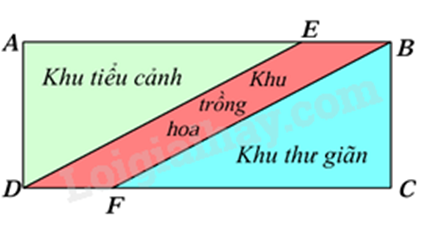
a) \(x\left( {70 - x} \right) = 250\).
b) Chiều dài mảnh vườn là 25m, chiều rộng là 10m.
c) Diện tích khu tiểu cảnh là 60 m2.
d) Người chủ vườn đã thuê người trồng hoa ở khu trồng hoa với chi phí là 50 000 đồng/\({m^2}\) thì số tiền chủ vườn phải trả cho người trồng hoa để trồng hết khu vườn hoa đó là \(3{\rm{ }}000{\rm{ }}000\) đồng.
Minh thực hiện thí nghiệm với một cốc thủy tinh có dạng hình trụ, đường kính đáy 6 cm, chiều cao 10 cm. Minh bỏ một quả bóng bàn (đường kính 40 mm) vào cốc và rót thêm 200 \(c{m^3}\) nước, sau đó mức nước dâng lên đến 7,2 cm. (lấy \(\pi \approx 3,14\), làm tròn các kết quả đến hàng phần trăm)
a) Lượng nước tối đa mà chiếc cốc thuỷ tinh có thể chứa là \(282,6c{m^3}\).
b) Thể tích của quả bóng bàn là khoảng 33,49 cm³.
c) Thể tích phần nổi của quả bóng bàn chiếm khoảng 10,36% tổng thể tích của nó.
d) Nếu quả bóng bàn bị nhấn chìm hoàn toàn, mức nước trong cốc sẽ cao hơn 7,5 cm.
Cho hàm số \(y = - 3{x^2}\). Có bao nhiêu điểm thuộc đồ thị của hàm số mà có tung độ bằng -1?
Đáp án:
Sau khi điều tra về thời gian tự học buổi tối của học sinh lớp 9A có 30 học sinh, ta có bảng tần số tương đối ghép nhóm sau:
Số học sinh tự học từ 1 tiếng trở lên bằng bao nhiêu?
Đáp án:
Một bó hoa gồm 2 bông hoa màu đỏ, 1 bông hoa màu hồng và 1 bông hoa màu vàng. Bạn An chọn ngẫu nhiên 2 bông hoa từ bó hoa đó. Số kết quả thuận lợi cho biến cố “Trong 2 bông hoa được chọn ra, có duy nhất 1 bông hoa màu đỏ” là bao nhiêu?
Đáp án:
Cho ngũ giác đều ABCDE và một điểm P sao cho \(\Delta DPE\) đều . Số đo \(\widehat {APC}\) bằng bao nhiêu độ?
Đáp án:
Lời giải và đáp án
-
A.
\(2\).
-
B.
\( - 2\).
-
C.
\(\frac{1}{2}\).
-
D.
\(\frac{{ - 1}}{2}\).
Đáp án : B
Từ đồ thị hàm số xác định toạ độ một điểm thuộc đồ thị hàm số.
Thay toạ độ của điểm vào hàm số để tìm a.
Quan sát đồ thị hàm số ta thấy điểm (1;-2) thuộc đồ thị hàm số \(y = a{x^2}\).
Thay \(x = 1;y = - 2\) vào hàm số \(y = a{x^2}\), ta được:
\( - 2 = a{.1^2}\) suy ra \(a = - 2\).
Đáp án B
Trong các phương trình sau, phương trình nào là phương trình bậc hai một ẩn?
-
A.
\(2x - 4 = 0\).
-
B.
\({x^2} + 2x + 1 = 0\).
-
C.
\({x^2} - \sqrt x + 4 = 0\).
-
D.
\(0{x^2} + 2x - 4 = 0\).
Đáp án : B
Phương trình bậc hai một ẩn là phương trình có dạng \(a{x^2} + bx + c = 0\) \((a \ne 0)\) với a, b, c là các hệ số, x là ẩn.
Trong các phương trình trên, chỉ có phương trình \({x^2} + 2x + 1 = 0\) là phương trình bậc hai một ẩn.
Đáp án B
Tìm hai số, biết tổng của chúng bằng 23 và tích của chúng bằng 120. Vậy hai số cần tìm:
-
A.
23 và 120.
-
B.
10 và 8.
-
C.
15 và 8.
-
D.
15 và 18.
Đáp án : C
Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là hai nghiệm của phương trình bậc hai:
\({x^2} - Sx + P = 0\)
Giải phương trình để tìm hai số.
Vì hai số có tổng bằng 23 và tích bằng 120 nên hai số đó là nghiệm của phương trình bậc hai \({x^2} - 23x + 120 = 0\).
Giải phương trình ta được hai nghiệm \({x_1} = 15;{x_2} = 8\).
Đáp án C
Cho bảng tần số tương đối ghép nhóm về thời gian đi từ nhà đến trường của học sinh lớp \(9A\) như sau:
Để vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng, ta dùng giá trị nào đại diện cho nhóm số liệu \(\left[ {20;30} \right)\).
-
A.
\(5\).
-
B.
\(15\).
-
C.
\(25\).
-
D.
\(20\).
Đáp án : C
Giá trị đại diện cho nhóm số liệu \({\rm{[}}a;b)\) là \(\frac{{a + b}}{2}\).
Giá trị đại diện cho nhóm số liệu \(\left[ {20;30} \right)\) là: \(\frac{{20 + 30}}{2} = 25\).
Đáp án C
Một hộp chứa 4 quả cầu cùng loại trong đó có 1 quả cầu đỏ, 1 quả cầu xanh và 2 quả cầu vàng. Chọn ngẫu nhiên đồng thời ra hai quả cầu. Xác suất của biến cố “Chọn được 1 quả cầu đỏ và 1 quả cầu vàng” là
-
A.
\(\frac{1}{6}\).
-
B.
\(\frac{1}{4}\).
-
C.
\(\frac{1}{3}\).
-
D.
\(\frac{2}{3}\).
Đáp án : C
Xác định số phần tử của không gian mẫu.
Xác định các kết quả thuận lợi cho biến cố.
Khi đó xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố và số phần tử của không gian mẫu.
Gọi các quả cầu đỏ, xanh, 2 quả cầu vàng lần lượt là Đ, X, V1, V2.
Không gian mẫu của phép thử là:
\(\Omega = \){ĐX, ĐV1, ĐV2, XV1, XV2, V1V2}
Không gian mẫu có 6 phần tử.
Kết quả thuận lợi cho biến cố “Chọn được 1 quả cầu đỏ và 1 quả cầu vàng” là: ĐV1, ĐV2.
Có 2 kết quả thuận lợi cho biến cố.
Vậy xác suất của biến cố “Chọn được 1 quả cầu đỏ và 1 quả cầu vàng” là: \(\frac{2}{6} = \frac{1}{3}\).
Đáp án C
Cho tam giác ABC vuông tại A, có \(AB = 24\) cm, \(AC = 18\) cm. Chu vi đường tròn ngoại tiếp tam giác ABC bằng
-
A.
\(30\pi {\rm{cm}}\).
-
B.
\(225\pi {\rm{cm}}\).
-
C.
\(60\pi {\rm{cm}}\).
-
D.
\(15\pi {\rm{cm}}\).
Đáp án : A
Tính cạnh huyền của tam giác bằng định lí Pythagore.
Cạnh huyền chính là đường kính của đường tròn ngoại tiếp .
Sử dụng công thức tính chu vi đường tròn: \(C = 2\pi r = d\pi \).
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:
\(B{C^2} = A{B^2} + A{C^2} = {24^2} + {18^2} = 900\) suy ra \(BC = \sqrt {900} = 30\left( {cm} \right)\)
BC chính là đường kính của đường tròn ngoại tiếp tam giác ABC nên chu vi đường tròn là: \(C = 30\pi \left( {cm} \right)\).
Đáp án A
Độ dài bán kính đường tròn ngoại tiếp hình vuông có cạnh bằng 4 cm là:
-
A.
\(3\sqrt 2 cm\).
-
B.
\(4\sqrt 2 cm\).
-
C.
\(\sqrt 2 cm\).
-
D.
\(2\sqrt 2 cm\).
Đáp án : D
- Sử dụng định lí Pythagore để tính đường chéo của hình vuông.
- Đường tròn ngoại tiếp của hình vuông có tâm là giao điểm của hai đường chéo và bán kính bằng một nửa độ dài đường chéo.
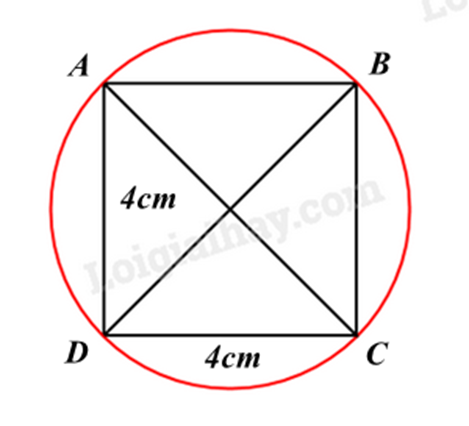
Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:
\(A{C^2} = A{B^2} + B{C^2} = {4^2} + {4^2} = 32\) suy ra \(AC = \sqrt {32} = 4\sqrt 2 \left( {cm} \right)\)
Khi đó độ dài bán kính đường tròn ngoại tiếp hình vuông ABCD là: \(\frac{{4\sqrt 2 }}{2} = 2\sqrt 2 \)(cm)
Đáp án D
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
Đáp án : B
Đa giác đều là một đa giác lồi có các cạnh bằng nhau và các góc bằng nhau.
Hình 1, Hình 3, Hình 4 không phải đa giác lồi nên không phải đa giác đều.
Hình 2 là đa giác đều.
Đáp án B
Phép quay nào với O là tâm biến tam giác đều thành chính nó?
-
A.
\(90^\circ \).
-
B.
\(100^\circ \).
-
C.
\(110^\circ \).
-
D.
\(120^\circ \).
Đáp án : D
Các phép quay thuận chiều hoặc ngược chiều \(\alpha ^\circ \) tâm O biến n-giác đều thành chính nó với \(\alpha ^\circ \) nhận các giá trị: \(\frac{{k.360^\circ }}{n}\) với \(k = 1;2;..;n\).
Các phép quay thuận chiều hoặc ngược chiều \(\alpha ^\circ \) tâm O biến tam giác đều thành chính nó với \(\alpha ^\circ \) nhận các giá trị: \(\frac{{360^\circ }}{3} = 120^\circ ;\frac{{2.360^\circ }}{3} = 240^\circ ;\frac{{3.360^\circ }}{3} = 360^\circ \) nên ta chọn đáp án D.
Đáp án D
Cho hình trụ sau. Cạnh AB quét nên mặt xung quanh của hình trụ, mỗi vị trí của cạnh AB gọi là:
-
A.
Đường sinh.
-
B.
Bán kính đáy.
-
C.
Chiều cao.
-
D.
Đường kính đáy.
Đáp án : A
Dựa vào kiến thức về hình trụ.
Theo đặc điểm của hình trụ thì cạnh AB quét nên mặt xung quanh của hình trụ, mỗi vị trí của cạnh AB được gọi là một đường sinh.
Đáp án A
Cho hình nón có bán kính đáy \(r = 2cm\). Biết diện tích xung quanh của hình nón là \(2\sqrt 5 \pi c{m^3}\), tính thể tích của hình nón.
-
A.
\(\pi c{m^3}\).
-
B.
\(\frac{5}{3}\pi c{m^3}\).
-
C.
\(\frac{4}{3}\pi {\rm{c}}{{\rm{m}}^{\rm{3}}}\).
-
D.
\(\frac{2}{3}\pi {\rm{c}}{{\rm{m}}^{\rm{3}}}\).
Đáp án : C
Sử dụng công thức tính diện tích xung quanh \({S_{xq}} = \pi rl\) để tìm đường sinh.
Áp dụng công thức liên hệ \({l^2} = {r^2} + {h^2}\) để tính chiều cao của hình nón.
Khi đó ta tính được thể tích của hình nón: \(V = \frac{1}{3}\pi {r^2}h\).
Vì diện tích xung quanh của hình nón bằng \(2\sqrt 5 \pi c{m^3}\) nên ta có:
\({S_{xq}} = \pi rl\)
hay \(2\sqrt 5 \pi = \pi .2.l\)
suy ra \(l = \frac{{2\sqrt 5 \pi }}{{2\pi }} = \sqrt 5 \).
Ta lại có: \({l^2} = {r^2} + {h^2}\) hay \({\left( {\sqrt 5 } \right)^2} = {2^2} + {h^2}\)
suy ra \({h^2} = 5 - 4 = 1\) do đó \(h = 1\).
Vậy thể tích của hình nón là: \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.2^2}.1 = \frac{4}{3}\pi \)\(c{m^3}\).
Đáp án C
-
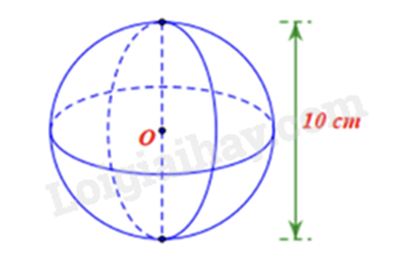
A.
\(\sqrt {10} cm.\)
-
B.
\(5cm.\)
-
C.
\(10cm.\)
-
D.
\(20cm.\)
Đáp án : B
Tính bán kính dựa vào đường kính.
Bán kính của hình cầu là: \(R = \frac{{10}}{2} = 5\left( {cm} \right)\)
Đáp án B
Một mảnh vườn hình chữ nhật ABCD có chu vi và diện tích lần lượt là 70 m và 250 \({m^2}\). Người ta chia mảnh vườn đó thành ba khu vực: khu tiểu cảnh ADE, khu trồng hoa BEDF, khu thư giãn BCF với \(BE = DF = 6m\) như mô tả ở hình bên. Gọi chiều dài của mảnh vườn của \(x\left( m \right),x > 0\).
a) \(x\left( {70 - x} \right) = 250\).
b) Chiều dài mảnh vườn là 25m, chiều rộng là 10m.
c) Diện tích khu tiểu cảnh là 60 m2.
d) Người chủ vườn đã thuê người trồng hoa ở khu trồng hoa với chi phí là 50 000 đồng/\({m^2}\) thì số tiền chủ vườn phải trả cho người trồng hoa để trồng hết khu vườn hoa đó là \(3{\rm{ }}000{\rm{ }}000\) đồng.
a) \(x\left( {70 - x} \right) = 250\).
b) Chiều dài mảnh vườn là 25m, chiều rộng là 10m.
c) Diện tích khu tiểu cảnh là 60 m2.
d) Người chủ vườn đã thuê người trồng hoa ở khu trồng hoa với chi phí là 50 000 đồng/\({m^2}\) thì số tiền chủ vườn phải trả cho người trồng hoa để trồng hết khu vườn hoa đó là \(3{\rm{ }}000{\rm{ }}000\) đồng.
a) Gọi chiều dài của mảnh vườn của \(x\left( m \right)\). Điều kiện: \(x > 0\).
Tính nửa chu vi của mảnh vườn, suy ra chiều rộng của mảnh vườn theo \(x\).
Suy ra phương trình diện tích của mảnh vườn là 250 \({m^2}\).
b) Giải phương trình diện tích để tính chiều dài, chiều rộng.
c) Chứng minh khu trồng hoa BEDF là hình bình hành.
Tính diện tích hình bình hành: \({S_{hbh}} = \) chiều cao.cạnh đáy
d) Tính số tiền chủ vườn phải trả cho người trồng hoa để trồng hết khu vườn hoa:
= Diện tích vườn hoa . 50 000
a) Sai
Gọi chiều dài của mảnh vườn của \(x\left( m \right)\). Điều kiện: \(x > 0\).
Nửa chu vi của mảnh vườn là: 70 : 2 = 35 (m)
Chiều rộng của mảnh vườn là: \(35 - x\) (m)
Do diện tích của mảnh vườn là 250 \({m^2}\) nên ta có phương trình:
\(x\left( {35 - x} \right) = 250\)
b) Đúng
Giải phương trình \(x\left( {35 - x} \right) = 250\) ta được:
\({x^2} - 35x + 250 = 0\)
\({x_1} = 25;{x_2} = 10\)
Vậy chiều dài của mảnh vườn là 25 m và chiều rộng là 10 m.
c) Đúng
Do khu trồng hoa có BE = DF = 6 m và BE // DF nên khu trồng hoa BEDF là hình bình hành.
Diện tích hình bình hành là: \(6.10 = 60\left( {{m^2}} \right)\)
d) Đúng
Số tiền chủ vườn phải trả cho người trồng hoa để trồng hết khu vườn hoa đó là:
\(60.{\rm{ }}50{\rm{ }}000 = 3{\rm{ }}000{\rm{ }}000\) (đồng).
Đáp án: SĐĐĐ
Minh thực hiện thí nghiệm với một cốc thủy tinh có dạng hình trụ, đường kính đáy 6 cm, chiều cao 10 cm. Minh bỏ một quả bóng bàn (đường kính 40 mm) vào cốc và rót thêm 200 \(c{m^3}\) nước, sau đó mức nước dâng lên đến 7,2 cm. (lấy \(\pi \approx 3,14\), làm tròn các kết quả đến hàng phần trăm)
a) Lượng nước tối đa mà chiếc cốc thuỷ tinh có thể chứa là \(282,6c{m^3}\).
b) Thể tích của quả bóng bàn là khoảng 33,49 cm³.
c) Thể tích phần nổi của quả bóng bàn chiếm khoảng 10,36% tổng thể tích của nó.
d) Nếu quả bóng bàn bị nhấn chìm hoàn toàn, mức nước trong cốc sẽ cao hơn 7,5 cm.
a) Lượng nước tối đa mà chiếc cốc thuỷ tinh có thể chứa là \(282,6c{m^3}\).
b) Thể tích của quả bóng bàn là khoảng 33,49 cm³.
c) Thể tích phần nổi của quả bóng bàn chiếm khoảng 10,36% tổng thể tích của nó.
d) Nếu quả bóng bàn bị nhấn chìm hoàn toàn, mức nước trong cốc sẽ cao hơn 7,5 cm.
a) Tính bán kính đáy cốc thuỷ tinh.
Tính thể tích của chiếc cốc thuỷ tinh: \(V = \pi {r^2}h\)
b) Tính bán kính quả bóng bàn.
Tính thể tích quả bóng bàn: \(V = \frac{4}{3}\pi {r^3}\)
c) Tính thể tích nước và phần chìm của quả bóng bàn trong cốc: \(V = \pi .{r^2}.h\)
Khi đó thể tích phần chìm của quả bóng bàn trong cốc bằng thể tích nước và phần chìm của quả bóng – thể tích nước.
Tính thể tích phần nổi của quả bóng bàn: thể tích quả bóng bàn – thể tích phần chìm
Tính tỉ số phần trăm thể tích phần nổi với thể tích quả bóng.
d) Nếu quả bóng bàn bị nhấn chìm hoàn toàn thì ta tính thể tích nước và thể tích quả bóng bàn.
Mức nước = thể tích nước và thể tích quả bóng bàn : diện tích đáy của chiếc cốc.
a) Đúng
Bán kính đáy cốc thuỷ tinh là: \(6:2 = 3\left( {cm} \right)\)
Thể tích của chiếc cốc thuỷ tinh là: \(V = \pi {r^2}h = 3,{14.3^2}.10 = 282,6\left( {c{m^3}} \right)\)
b) Đúng
Bán kính quả bóng bàn là: \(40:2 = 20\left( {mm} \right) = 2\left( {cm} \right)\)
Thể tích quả bóng bàn là: \({V_{bb}} = \frac{4}{3}\pi {r^3} = \frac{4}{3}.3,{14.2^3} \approx 33,49\left( {c{m^3}} \right)\)
c) Sai
Thể tích nước và phần chìm của quả bóng bàn trong cốc là:
\(V = \pi .{r^2}.h = 3,{14.3^2}.7,2 \approx 203,47\left( {c{m^3}} \right)\)
Khi đó thể tích phần chìm của quả bóng bàn trong cốc là:
\(203,47 - 200 = 3,47\left( {c{m^3}} \right)\).
Do đó thể tích phần nổi của quả bóng bàn là:
\(33,49 - 3,47 = 30,02\left( {c{m^3}} \right)\)
Thể tích phần nổi chiếm \(\frac{{30,02}}{{33,49}}.100\% \approx 89,64\% \) thể tích quả bóng.
d) Đúng
Nếu quả bóng bàn bị nhấn chìm hoàn toàn thì thể tích nước và thể tích quả bóng bàn là:
\(200 + 33,49 = 233,49\left( {c{m^3}} \right)\).
Khi đó mức nước là: \(\frac{{233,49}}{{\pi {r^2}}} = \frac{{233,49}}{{3,{{14.3}^2}}} \approx 8,26\left( {cm} \right) > 7,5\left( {cm} \right)\) nên D đúng.
Đáp án: ĐĐSĐ
Cho hàm số \(y = - 3{x^2}\). Có bao nhiêu điểm thuộc đồ thị của hàm số mà có tung độ bằng -1?
Đáp án:
Đáp án:
Thay tung độ \(y = - 1\) vào hàm số \(y = - 3{x^2}\) để tìm \(x\).
Thay \(y = - 1\) vào \(y = - 3{x^2}\), ta được:
\(\begin{array}{l} - 1 = - 3{x^2}\\{x^2} = \frac{1}{3}\\x = \pm \frac{{\sqrt 3 }}{3}\end{array}\)
Nên hai điểm \(\left( {\frac{{\sqrt 3 }}{3}; - 1} \right);\left( { - \frac{{\sqrt 3 }}{3}; - 1} \right)\) thuộc đồ thị của hàm số.
Đáp án: 2
Sau khi điều tra về thời gian tự học buổi tối của học sinh lớp 9A có 30 học sinh, ta có bảng tần số tương đối ghép nhóm sau:
Số học sinh tự học từ 1 tiếng trở lên bằng bao nhiêu?
Đáp án:
Đáp án:
Xác định tần số tương đối của số học sinh tự học từ 1 tiếng trở lên.
Từ đó tính số học sinh khi biết tỉ số phần trăm của số học sinh đó.
Vì 60 phút = 1 tiếng nên số học sinh tự học từ 1 tiếng trở lên tương ứng với tổng tần số tương đối của nhóm [60;90) và [90;120).
Do đó tần số tương đối của số học sinh tự học từ 1 tiếng trở lên là: 20% + 30% = 50%
Số học sinh tự học từ 1 tiếng trở lên là: \(30.50\% = 15\) (học sinh)
Đáp án: 15
Một bó hoa gồm 2 bông hoa màu đỏ, 1 bông hoa màu hồng và 1 bông hoa màu vàng. Bạn An chọn ngẫu nhiên 2 bông hoa từ bó hoa đó. Số kết quả thuận lợi cho biến cố “Trong 2 bông hoa được chọn ra, có duy nhất 1 bông hoa màu đỏ” là bao nhiêu?
Đáp án:
Đáp án:
Liệt kê các phần tử của không gian mẫu.
Liệt kê các kết quả thuận lợi cho biến cố “Trong 2 bông hoa được chọn ra, có duy nhất 1 bông hoa màu đỏ”.
Kí hiệu: Bông hoa màu đỏ: Đ1, Đ2
Bông hoa màu hồng: H
Bông hoa màu vàng: V
Không gian mẫu là:
\(\Omega \) = {(Đ1, Đ2), (Đ1, H), (Đ1, V), (Đ2, H), (Đ2, V), (H, V)}
Trong các kết quả trên, các kết quả thuận lợi cho biến cố “Trong 2 bông hoa được chọn ra, có duy nhất 1 bông hoa màu đỏ” là: (Đ1, H), (Đ1, V), (Đ2, H), (Đ2, V).
Vậy có 4 kết quả thuận lợi cho biến cố “Trong 2 bông hoa được chọn ra, có duy nhất 1 bông hoa màu đỏ”.
Đáp án: 4
Cho ngũ giác đều ABCDE và một điểm P sao cho \(\Delta DPE\) đều . Số đo \(\widehat {APC}\) bằng bao nhiêu độ?
Đáp án:
Đáp án:
Đa giác đều có n cạnh bằng nhau và cũng có n góc bằng nhau nên có công thức tính số đo mỗi góc là: \(\frac{{\left( {n - 2} \right).180^\circ }}{n}\).
Sử dụng tính chất góc của tam giác đều để tính góc của tam giác đều DPE.
Suy ra \(\widehat {AEP} = \widehat {CDP}\).
Chứng minh \(\Delta AEP,\Delta CDP\) cân suy ra số đo các góc \(\widehat {APE} = \widehat {CPD}\).
Từ đó tính được \(\widehat {APC} = 360^\circ - \widehat {EPD} - \widehat {APE} - \widehat {CPD}\)
Số đo mỗi góc của ngũ giác đều là: \(\frac{{\left( {5 - 2} \right).180^\circ }}{5} = 108^\circ \).
Vì \(\Delta DPE\) đều nên số đo \(\widehat {EPD} = \widehat {EDP} = \widehat {DEP} = 60^\circ \).
Ta có: \(\widehat {AEP} = \widehat {CDP} = 108^\circ - 60^\circ = 48^\circ \).
Vì ABCDE là ngũ giác đều và \(\Delta DPE\) đều nên AE = ED = EP = PD = DC.
Do đó \(\Delta AEP,\Delta CDP\) cân nên \(\widehat {APE} = \widehat {CPD} = \left( {180^\circ - 48^\circ } \right):2 = 66^\circ \).
Vậy \(\widehat {APC} = 360^\circ - 60^\circ - 2.66^\circ = 168^\circ \).
Đáp án: 168
a) Biểu diễn điểm có tung độ gấp 2 lần hoành độ.
Thay vào hàm số \(y = \frac{{ - 1}}{4}{x^2}\) để tìm M.
b) Dùng \(ac < 0\) để xác định số nghiệm của phương trình.
Tính tổng và tích của hai nghiệm \({x_1},{x_2}\) theo định lí Viète: \(\left\{ \begin{array}{l}S = {x_1} + {x_2} = \frac{{ - b}}{a}\\P = {x_1}{x_2} = \frac{c}{a}\end{array} \right.\).
Biến đổi biểu thức để xuất hiện tổng và tích của hai nghiệm.
a) Điểm có tung độ gấp 2 lần hoành độ có toạ độ \(M\left( {{x_0};{y_0}} \right) = M\left( {{x_0};2{x_0}} \right)\)
Vì \({y_0} = 2{x_0}\) nên \( - \frac{1}{4}{x_0}^2 = 2{x_0}\)
\( - \frac{1}{4}{x_0}^2 - 2{x_0} = 0\)
\({x_0}^2 + 8{x_0} = 0\)
\({x_0}\left( {{x_0} + 8} \right) = 0\)
\({x_0} = 0\) hoặc \({x_0} = - 8\)
suy ra \({y_0} = 0\) hoặc \({y_0} = - 16\)
Ta được \(M\left( {0;0} \right)\) (loại) hoặc \(M\left( { - 8; - 16} \right)\).
Vậy \(M\left( { - 8; - 16} \right)\).
b) Vì \(ac = 1.\left( { - 10} \right) = - 10 < 0\) nên phương trình có hai nghiệm phân biệt \({x_1};{x_2}\).
Áp dụng định lí Viète, ta có:
\(\left\{ \begin{array}{l}S = {x_1} + {x_2} = \frac{{ - \left( { - 1} \right)}}{1} = 1\\P = {x_1}{x_2} = \frac{{ - 10}}{1} = - 10\end{array} \right.\)
Ta có:
\(\begin{array}{l}x_1^3 + x_2^3 = \left( {{x_1} + {x_2}} \right)\left( {x_1^2 - {x_1}{x_2} + x_2^2} \right)\\ = \left( {{x_1} + {x_2}} \right)\left( {x_1^2 + 2{x_1}{x_2} + x_2^2 - 3{x_1}{x_2}} \right)\\ = \left( {{x_1} + {x_2}} \right)\left[ {\left( {x_1^2 + 2{x_1}{x_2} + x_2^2} \right) - 3{x_1}{x_2}} \right]\\ = \left( {{x_1} + {x_2}} \right)\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 3{x_1}{x_2}} \right]\\ = 1.\left[ {{1^2} - 3.\left( { - 10} \right)} \right]\\ = 1 + 30\\ = 31\end{array}\)
Vậy \(x_1^3 + x_2^3 = 31\).
a) Chứng minh \(\Delta ABD\) và \(\Delta ABF\) nội tiếp đường tròn đường kính AB nên bốn điểm A, B, D, F cùng thuộc 1 đường tròn đường kính AB hay tứ giác ABDF nội tiếp đường tròn đường kính AB.
b) Chứng minh $\Delta ADB~\backsim \Delta ACE$ (g.g) suy ra \(\frac{{AD}}{{AC}} = \;\frac{{AB}}{{AE}}\) nên AD.AE = AC.AB
c) Chứng minh \(\widehat {DFE} = \widehat {AEC}\) suy ra DF // EC và EC \( \bot \) AC nên DF \( \bot \) AC
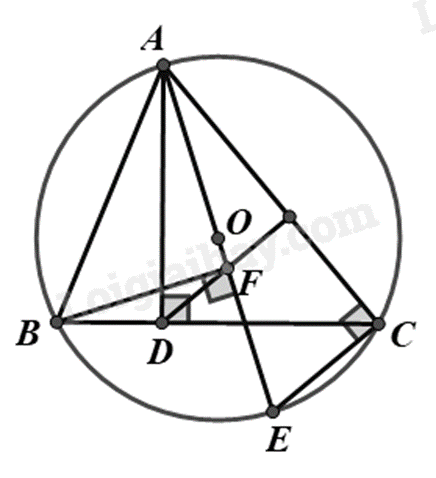
a) Xét \(\Delta ABD\) vuông tại D \(\left( {AD \bot BD} \right)\) nên \(\Delta ABD\) nội tiếp đường tròn đường kính AB, suy ra A, B, D thuộc đường tròn đường kính AB.
Xét \(\Delta ABF\) vuông tại F \(\left( {AF \bot BF} \right)\) nên \(\Delta ABF\) nội tiếp đường tròn đường kính AB, suy ra A, B, F thuộc đường tròn đường kính AB.
Do đó A, B, D, F cùng thuộc đường tròn đường kính AB hay tứ giác ABDF nội tiếp đường tròn đường kính AB.
b) Vì \(\widehat {ACE} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \(\Delta AEC\) vuông tại C.
Xét \(\Delta ABD\) và \(\Delta AEC\) có:
\(\widehat {ADB} = \widehat {ACE}\left( { = 90^\circ } \right)\)
\(\widehat {ABD} = \widehat {AEC}\) (hai góc nội tiếp chắn cung AC)
nên $\Delta ABD\backsim \Delta AEC\left( g.g \right)$
suy ra \(\frac{{AD}}{{AB}} = \;\frac{{AC}}{{AE}}\) nên \(AD.AE = AC.AB\).
c) Vì ABDF là tứ giác nội tiếp nên \(\widehat {AFD} + \widehat {ABD} = 180^\circ \) (tổng hai góc đối của tứ giác nội tiếp)
Mà \(\widehat {AFD} + \widehat {DFE} = 180^\circ \) (hai góc kề bù) nên \(\widehat {ABD} = \widehat {DFE}\)
Kết hợp với \(\widehat {ABD} = \widehat {AEC}\) (hai góc nội tiếp chắn cung AC)
Suy ra \(\widehat {DFE} = \widehat {AEC}\)
Mà hai góc này ở vị trí so le trong nên DF // CE.
Mà \(EC \bot AC\) (\(\widehat {ACE} = 90^\circ \)) nên \(DF \bot AC\).
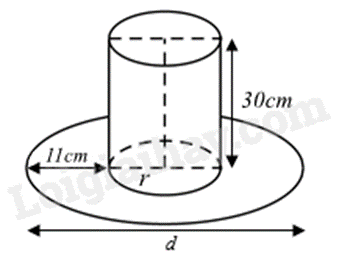
Biểu diễn d bằng biểu thức chứa r.
Tính diện tích vải để may phần dạng hình trụ:
\({S_1}\) = diện tích xung quanh hình trụ + diện tích 1 đáy của hình trụ.
Tính diện tích vải để may phần dạng hình vành khuyên:
\({S_2}\) = \({S_{vk}} = \pi \left( {{R^2} - {r^2}} \right)\,\left( {R > r} \right)\)
Khi đó ta viết được biểu thức P.
Biến đổi biểu thức về dạng \(P = \pi \left[ {A - f{{\left( x \right)}^2}} \right] \le A\pi \). Khi đó giá trị lớn nhất của P là A khi \(f\left( x \right) = 0\).
Ta có: \(d = 2.11 + 2r = 2r + 22\left( {cm} \right)\)
Diện tích vải để may phần dạng hình trụ là:
\({S_1} = 2\pi rh + \pi {r^2} = 2.30.\pi r + \pi {r^2} = 60\pi r + \pi {r^2}\left( {c{m^2}} \right)\)
Diện tích vải để may phần dạng hình vành khuyên là:
\({S_2} = \pi \left[ {{{\left( {r + 11} \right)}^2} - {r^2}} \right] = \pi \left( {22r + 121} \right)\left( {c{m^2}} \right)\)
Khi đó biểu thức P là:
\(\begin{array}{l}P = 3{S_2} - {S_1}\\ = 3\pi \left( {22r + 121} \right) - 60\pi r - \pi {r^2}\\ = 66\pi r + 363\pi - 60\pi r - \pi {r^2}\\ = 363\pi + 6\pi r - \pi {r^2}\\ = \pi \left( {363 + 6r - {r^2}} \right)\\ = \pi \left[ { - {r^2} + 6r - 9 + 372} \right]\\ = \pi \left[ { - {{\left( {r - 3} \right)}^2} + 372} \right] \le 372\pi \end{array}\)
Dấu “=” xảy ra khi \(r - 3 = 0\) suy ra \(r = 3\). Khi đó P đạt giá trị lớn nhất.
Suy ra \(d = 2.3 + 22 = 6 + 22 = 28\left( {cm} \right)\).
Vậy tổng \(r + d = 3 + 28 = 31\) thì P đạt giá trị lớn nhất là \(372\pi \).
