 Toán lớp 6 - Giải toán lớp 6 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
Toán lớp 6 - Giải toán lớp 6 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
 Đề thi học kì 2 của các trường có lời giải – Mới nhất
Đề thi học kì 2 của các trường có lời giải – Mới nhất
Đề thi học kì 2 môn toán lớp 6 năm 2019 - 2020 Sở GD tỉnh Nam Định
Giải chi tiết đề thi học kì 2 môn toán lớp 6 năm 2019 - 2020 Sở GD tỉnh Nam Định với cách giải nhanh và chú ý quan trọng
Đề bài
PHẦN I: TRẮC NGHIỆM (4 điểm).
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước phương án đó vào bài làm
Câu 1. Góc vuông có số đo bằng giá trị nào sau đây?
A. \({60^0}\) B. \({90^0}\)
C. \({180^0}\) D. \({45^0}\)
Câu 2. Viết số \( - 3\dfrac{2}{3}\) dưới dạng một phân số ta được kết quả là:
A. \(\dfrac{{ - 2}}{1}\) B. \(\dfrac{{ - 7}}{3}\)
C. \(\dfrac{{ - 9}}{3}\) D. \(\dfrac{{ - 11}}{3}\)
Câu 3. Cho 5 điểm phân biệt. Vẽ các đoạn nối hai điểm trong 5 điểm đó với nhau. Tổng số đoạn thẳng vẽ được là
A. \(10\) B. \(9\)
C. \(8\) D. \(5\)
Câu 4. Trên tia \(Ox\) lấy hai điểm \(A\) và \(B\) sao cho \(OA = 3cm,OB = 5cm\). Khi đó, độ dài của đoạn thẳng \(AB\) là:
A. \(8cm\) B. \(5cm\)
C. \(3cm\) D. \(2cm\)
Câu 5. Phân số nghịch đảo của phân số \(\dfrac{5}{6}\) là
A. \(\dfrac{6}{5}\) B. \(\dfrac{5}{{ - 6}}\)
C. \(\dfrac{{ - 5}}{6}\) D. \(\dfrac{{ - 6}}{5}\)
Câu 6. Số đối của số \(\dfrac{{ - 2}}{3}\) là
A. \(\dfrac{{ - 3}}{2}\) B. \(\dfrac{3}{2}\)
C. \(\dfrac{2}{3}\) D. \(\dfrac{2}{{ - 3}}\)
Câu 7. Viết kết quả phép tính \({2^3}.4\) dưới dạng một lũy thừa ta được:
A. \({2^6}\) B. \({2^5}\)
C. \({2^{12}}\) D. \({8^3}\)
Câu 8. Cho \(a = {3.5^2}.7\) và \(b = {2^2}{.3^2}.5\). Khi đó ƯCLN\(\left( {a;b} \right)\) bằng
A. \({3^2}{.5^2}\) B. \(2.3.5.7\)
C. \(3.5\) D. \({2^2}{.3^2}{.5^2}.7\)
Câu 9. Số nào sau đây chia hết cho cả 2 và 5?
A. \(2019\) B. \(2021\)
C. \(2020\) D. \(2022\)
Câu 10. Tập hợp nào sau đây chỉ gồm các phần tử là số nguyên tố?
A. \(\left\{ {1;3;5} \right\}\) B. \(\left\{ {2;3;5} \right\}\)
C. \(\left\{ {3;5;9} \right\}\) D. \(\left\{ {1;2;3} \right\}\)
Câu 11. Rút gọn phân số \(\dfrac{{ - 12}}{{18}}\), ta được phân số tối giản
A. \(\dfrac{{ - 2}}{3}\) B. \(\dfrac{{ - 6}}{9}\)
C. \(\dfrac{{ - 4}}{6}\) D. \(\dfrac{{ - 3}}{2}\)
Câu 12. Tổng tất cả các số nguyên \(x\) thỏa mãn \( - 3 \le x \le 3\) bằng
A. \(0\) B. \(1\)
C. \(2\) D. \(3\)
Câu 13. Cho \(m = {2^3}{.3.5^2}\) và \(n = 3.5.7\). Khi đó BCNN\(\left( {m;n} \right)\) bằng
A. \(3.5\) B. \({2^3}{.3^2}{.5^3}.7\)
C. \({3.5^2}\) D. \({2^3}{.3.5^2}.7\)
Câu 14. Lớp học của bạn An có tất cả 36 bạn. Biết số bạn nữ bằng \(\dfrac{3}{4}\) số học sinh của cả lớp. Số bạn nữ của lớp bạn An là:
A. \(27\) B. \(9\)
C. \(21\) D. \(12\)
Câu 15. Cho các điểm M, N, P cùng thuộc một đường thẳng như hình vẽ:
Hai tia đối nhau trong hình vẽ trên là:
A. tia PN và tia PM
B. tia MN và tia NP
C. tia PN và tia NM
D. tia NM và tia NP
Câu 16. Số nguyên \(x\) thỏa mãn điều kiện \(\dfrac{x}{3} = \dfrac{2}{6}\) là:
A. \(6\) B. \(2\)
C. \(1\) D. \(3\)
Câu 17. Cho tập hợp \(P = \left\{ {x \in \mathbb{N}|x < 4} \right\}\). Số phần tử của tập hợp \(P\) là
A. \(1\) B. \(4\)
C. \(3\) D. \(2\)
Câu 18. Cho biết M là điểm nằm giữa hai điểm H và K. Khi đó ta có
A. \(KM + KH = MH\)
B. \(HM + HK = MK\)
C. \(MH + MK = HK\)
D. \(MH = MK\)
Câu 19. Biết \(\dfrac{3}{5}\) của số \(a\) bằng \(45\). Số \(a\) là
A. \(9\) B. \(75\)
C. \(27\) D. \(15\)
Câu 20. Cho hai góc phụ nhau là \(xOy\) và \(mAn\), biết góc \(xOy\) bằng \({30^0}\). Khi đó số đo của góc \(mAn\) bằng
A. \({30^0}\) B. \({45^0}\)
C. \({120^0}\) D. \({60^0}\)
PHẦN II: TỰ LUẬN (6 điểm).
Bài 1: (1,5 điểm)
Thực hiện các phép tính:
a) \(\dfrac{{29}}{{15}} + \dfrac{{ - 5}}{{17}} + \dfrac{{ - 12}}{{17}} - \dfrac{{14}}{{15}}\)
b) \(\dfrac{{ - 3}}{4}.\dfrac{{11}}{{14}} + 3\dfrac{1}{2} + \dfrac{{ - 3}}{4}:\dfrac{{14}}{{17}}\)
Bài 2: (1 điểm)
Bác Bình đi xe đạp điện từ nhà đến cơ quan với vận tốc \(24km/h\) hết \(\dfrac{1}{3}\) giờ. Khi về, bác Bình đi với vận tốc \(28km/h\). Tính thời gian bác Bình đi từ cơ quan về nhà.
Bài 3: (2,5 điểm)
Trên cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia , vẽ hai tia \(Oy\) và \(Om\) sao cho góc \(xOy\) bằng \({80^0}\) và góc \(xOm\) bằng \({130^0}\).
a) Chứng minh tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Om\). Tính số đo của góc \(yOm\).
b) Vẽ tia \(Ot\) là tia đối của tia \(Ox\). Chứng minh tia \(Om\) là tia phân giác của góc \(yOt\).
Bài 4: (1 điểm)
a) Một trường học có số học sinh nhỏ hơn \(500\) em. Nếu toàn thể học sinh của trường xếp hàng 5, xếp hàng 6, xếp hàng 7 đều dư ra 3 bạn. Nếu toàn thể học sinh của trường xếp hàng 9 thì vừa đủ. Tính số học sinh của trường.
b) Cho \(P = \dfrac{{{{10}^{2018}} + 1}}{{{{10}^{2020}} + 1}}\) và \(Q = \dfrac{{{{10}^{2019}} + 1}}{{{{10}^{2021}} + 1}}\). Hãy so sánh \(P\) và \(Q\).
Đ/a TN
|
1B |
2D |
3A |
4D |
5A |
|
6C |
7B |
8C |
9C |
10B |
|
11A |
12A |
13D |
14A |
15D |
|
16C |
17B |
18C |
19B |
20D |
Câu 1 (NB):
Phương pháp:
Sử dụng định nghĩa góc vuông: Góc vuông là góc có số đo bằng \({90^0}\).
Cách giải:
Góc vuông là góc có số đo bằng \({90^0}\).
Chọn B
Câu 2 (TH):
Phương pháp:
Sử dụng phương pháp đổi hỗ số về phân số:
\( - a\dfrac{b}{c} = - \dfrac{{a.c + b}}{c}\)
Cách giải:
Ta có: \( - 3\dfrac{2}{3} = - \dfrac{{3.3 + 2}}{3} = - \dfrac{{11}}{3} = \dfrac{{ - 11}}{3}\)
Chọn D
Câu 3 (VD):
Phương pháp:
Vẽ hình và đếm.
Cách giải:
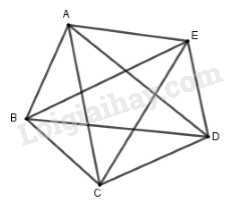
Các đoạn thẳng tạo thành là:
\(AB,AC,AD,AE,\) \(BC,BD,BE,CD,CE,\) \(DE\).
Vậy có tất cả \(10\) đoạn thẳng.
Chọn A
Câu 4 (TH):
Phương pháp:
Sử dụng công thức cộng đoạn thẳng:
Nếu điểm \(M\) nằm giữa hai điểm \(A\) và \(B\) thì: \(AM + MB = AB\)
Cách giải:
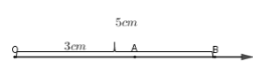
Trên tia \(Ox\) ta có: \(OA < OB\left( {3cm < 5cm} \right)\) nên điểm \(A\) nằm giữa hai điểm \(O\) và \(B\).
Khi đó \(OA + AB = OB\)
\(\begin{array}{l} \Rightarrow 3 + AB = 5\\\,\,\,\,\,\,\,\,\,\,\,\,\,AB = 5 - 3\\\,\,\,\,\,\,\,\,\,\,\,\,\,AB = 2\end{array}\)
Chọn D
Câu 5 (NB):
Phương pháp:
Phân số nghịch đảo của \(\dfrac{a}{b}\) là \(\dfrac{b}{a}\).
Cách giải:
Phân số nghịch đảo của phân số \(\dfrac{5}{6}\) là \(\dfrac{6}{5}\).
Chọn A
Câu 6 (NB):
Phương pháp:
Số đối của số \(a\) là \( - a\).
Cách giải:
Số đối của số \(\dfrac{{ - 2}}{3}\) là \(\dfrac{2}{3}\).
Chọn C
Câu 7 (NB):
Phương pháp:
Biến đổi các thừa số trong tích về lũy thừa cơ số \(2\).
Sử dụng công thức \({a^m}.{a^n} = {a^{m + n}}\).
Cách giải:
Ta có:
\({2^3}.4 = {2^3}{.2^2} = {2^{3 + 2}} = {2^5}\)
Chọn B
Câu 8 (NB):
Phương pháp:
Quy tắc lấy ước chung lớn nhất của hai số \(a,b\) sau khi đã phân tích \(a,b\) thành tích các thừa số nguyên tố:
- Chọn các số nguyên tố chung.
- Lấy tích các số nguyên tố đó kèm theo lũy thừa nhỏ nhất của chúng.
Cách giải:
\(a = {3.5^2}.7\)
\(b = {2^2}{.3^2}.5\)
\( \Rightarrow \) ƯCLN\(\left( {a;b} \right)\) \( = 3.5\)
Chọn C
Câu 9 (NB):
Phương pháp:
Số chia hết cho cả \(2\) và \(5\) thì có tận cùng bằng \(0\).
Cách giải:
Trong các số đã cho chỉ có số \(2020\) có tận cùng bằng \(0\) nên chia hết cho cả \(2\) và \(5\).
Chọn C
Câu 10 (NB):
Phương pháp:
Sử dụng bảng số nguyên tố loại đáp án.
Cách giải:
Đáp án A: loại vì \(1\) không là số nguyên tố.
Đáp án B: đúng.
Đáp án C: loại vì \(9\) là hợp số.
Đáp án D: loại vì \(1\) không là số nguyên tố.
Chọn B
Câu 11 (TH):
Phương pháp:
Chia cả tử và mẫu của phân số đã cho cho thừa số chung.
Cách giải:
\(\dfrac{{ - 12}}{{18}} = \dfrac{{ - 12:6}}{{18:6}} = \dfrac{{ - 2}}{3}\)
Chọn A
Chú ý:
Một số em có thể sẽ chỉ rút gọn như sau: \(\dfrac{{ - 12}}{{18}} = \dfrac{{ - 12:3}}{{18:3}} = \dfrac{{ - 4}}{6}\) hoặc \(\dfrac{{ - 12}}{{18}} = \dfrac{{ - 12:2}}{{18:2}} = \dfrac{{ - 6}}{9}\) rồi chọn các đáp án B, C là sai vì các phân số này chưa tối giản.
Câu 12 (TH):
Phương pháp:
Tìm các số nguyên \(x\) thỏa mãn và tính tổng.
Cách giải:
Vì \( - 3 \le x \le 3\) và \(x\) nguyên nên \(x \in \left\{ { - 3; - 2; - 1;0;1;2;3} \right\}\).
Vậy tổng các số nguyên \(x\) là: \(\left( { - 3} \right) + \left( { - 2} \right) + \left( { - 1} \right)\) \( + 0 + 1 + 2 + 3 = 0\)
Chọn A
Câu 13 (TH):
Phương pháp:
Muốn tìm BCNN của hai số \(m,n\) khi đã phân tích được chúng thành tích các thừa số nguyên tố, ta chỉ cần:
- Chọn tất cả các thừa số nguyên tố xuất hiện trong \(m,n\).
- Lấy tích các thừa số đó kèm theo lũy thừa lớn nhất của chúng.
Cách giải:
\(m = {2^3}{.3.5^2}\)
\(n = 3.5.7\)
\( \Rightarrow \) BCNN\(\left( {m;n} \right)\) \( = {2^3}{.3.5^2}.7\)
Chọn D
Câu 14 (NB):
Phương pháp:
\(\dfrac{a}{b}\) của số \(m\) là \(\dfrac{a}{b}.m\)
Cách giải:
Số bạn nữ của lớp An là:
\(\dfrac{3}{4}.36 = 27\) (bạn)
Chọn A
Câu 15 (NB):
Phương pháp:
Quan sát hình vẽ và nhận xét.
Cách giải:
Đáp án A: Tia PN và PM không đối nhau nên A sai.
Đáp án B: Tia MN và tia NP không chung gốc nên không đối nhau nên B sai.
Đáp án C: Tia PN và tia NM không chung gốc nên không đối nhau nên C sai.
Đáp án D: Tia NM và tia NP đối nhau.
Chọn D
Câu 16 (NB):
Phương pháp:
Sử dụng tính chất của phân số \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(ad = bc\)
Cách giải:
\(\begin{array}{l}\dfrac{x}{3} = \dfrac{2}{6}\\x.6 = 3.2\\x.6 = 6\\x = 6:6\\x = 1\end{array}\)
Chọn C
Câu 17 (TH):
Phương pháp:
Liệt kê và đếm số phần tử của P.
Cách giải:
\(\begin{array}{l}P = \left\{ {x \in \mathbb{N}|x < 4} \right\}\\\,\,\,\,\, = \left\{ {0;1;2;3} \right\}\end{array}\)
Vậy P có \(4\) phần tử.
Chọn B
Câu 18 (NB):
Phương pháp:
Nếu điểm \(M\) nằm giữa hai điểm \(A\) và \(B\) thì: \(AM + MB = AB\)
Cách giải:
M là điểm nằm giữa hai điểm H và K thì \(HM + MK = HK\).
Chọn C
Câu 19 (TH):
Phương pháp:
Muốn tìm một số biết \(\dfrac{a}{b}\) của nó bằng \(m\) ta lấy \(m\) chia cho \(\dfrac{a}{b}\).
Cách giải:
Số \(a\) là: \(45:\dfrac{3}{5} = 45.\dfrac{5}{3} = 75\)
Chọn B
Câu 20 (NB):
Phương pháp:
Hai góc phụ nhau có tổng bằng \({90^0}\).
Cách giải:
Góc \(xOy\) và \(mAn\) phụ nhau nên:
\(\begin{array}{l}\widehat {xOy} + \widehat {mAn} = {90^0}\\{30^0} + \widehat {mAn} = {90^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\widehat {mAn} = {90^0} - {30^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\widehat {mAn} = {60^0}\end{array}\)
Chọn D
LG bài 1
Phương pháp giải:
a) Sử dụng tính chất giao hoán, kết hợp để nhóm các số hạn thích hợp
b) Sử dụng tính chất \(a.b + a.c = a.\left( {b + c} \right)\)
Lời giải chi tiết:
a) \(\dfrac{{29}}{{15}} + \dfrac{{ - 5}}{{17}} + \dfrac{{ - 12}}{{17}} - \dfrac{{14}}{{15}}\)
\(\begin{array}{l} = \left( {\dfrac{{29}}{{15}} - \dfrac{{14}}{{15}}} \right) + \left( {\dfrac{{ - 5}}{{17}} + \dfrac{{ - 12}}{{17}}} \right)\\ = \dfrac{{15}}{{15}} + \dfrac{{ - 17}}{{17}}\\ = 1 + \left( { - 1} \right) = 0\end{array}\)
b) \(\dfrac{{ - 3}}{4}.\dfrac{{11}}{{14}} + 3\dfrac{1}{2} + \dfrac{{ - 3}}{4}:\dfrac{{14}}{{17}}\)
\(\begin{array}{l} = \dfrac{{ - 3}}{4}.\dfrac{{11}}{{14}} + \dfrac{9}{2} + \dfrac{{ - 3}}{4}.\dfrac{{17}}{{14}}\\ = \left( {\dfrac{{ - 3}}{4}.\dfrac{{11}}{{14}} + \dfrac{{ - 3}}{4}.\dfrac{{17}}{{14}}} \right) + \dfrac{9}{2}\\ = \dfrac{{ - 3}}{4}.\left( {\dfrac{{11}}{{14}} + \dfrac{{17}}{{14}}} \right) + \dfrac{9}{2}\\ = \dfrac{{ - 3}}{4}.\dfrac{{28}}{{14}} + \dfrac{9}{2}\\ = \dfrac{{ - 3}}{4}.2 + \dfrac{9}{2}\\ = \dfrac{{ - 3}}{2} + \dfrac{9}{2}\\ = \dfrac{6}{2} = 3\end{array}\)
LG bài 2
Phương pháp giải:
Sử dụng công thức: Quãng đường = vận tốc x thời gan
Tính quãng đường từ nhà đến cơ quan
Tính thời gian bác Bình đi từ cơ quan về nhà
Lời giải chi tiết:
Quãng đường từ nhà đến cơ quan bác Bình là:
\(24.\dfrac{1}{3} = 8km\)
Thời gian bác Bình đi từ cơ quan về nhà là:
\(\dfrac{8}{{28}} = \dfrac{2}{7}\) giờ
LG bài 3
Phương pháp giải:
a) Trên cùng một nửa mặt phẳng bờ chứa tia \(Oa\), nếu \(\widehat {mOa} < \widehat {nOa}\) thì tia Om nằm giữa hai tia On và Oa.
Sử dụng công thức cộng góc để tính toán
b) Tia Om là tia phân giác của góc \(aOb\) nếu tia Om nằm giữa hai tia Oa và Ob, đồng thời \(\widehat {mOa} = \widehat {mOb}\)
Lời giải chi tiết:
Trên cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia \(Ox\), vẽ hai tia \(Oy\) và \(Om\) sao cho góc \(xOy\) bằng \({80^0}\) và góc \(xOm\) bằng \({130^0}\).
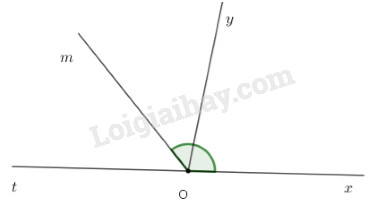
a) Chứng minh tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Om\). Tính số đo của góc \(yOm\).
Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat {xOy} < \widehat {xOm}\) \(\left( {{{80}^0} < {{130}^0}} \right)\) nên tia Oy nằm giữa hai tia Ox và Om.
Suy ra \(\widehat {xOy} + \widehat {yOm} = \widehat {xOm}\)
\( \Rightarrow \widehat {yOm} = \widehat {xOm} - \widehat {xOy}\) \( = {130^0} - {80^0} = {50^0}\)
Vậy \(\widehat {yOm} = {50^0}.\)
b) Vẽ tia \(Ot\) là tia đối của tia \(Ox\). Chứng minh tia \(Om\) là tia phân giác của góc \(yOt\).
Vì Ot là tia đối của tia Ox nên \(\widehat {xOm}\) và \(\widehat {mOt}\) là hai góc kề bù
Suy ra \(\widehat {xOm} + \widehat {mOt} = {180^0}\)
\( \Rightarrow \widehat {mOt} = {180^0} - \widehat {xOm}\) \( = {180^0} - {130^0} = {50^0}\)
Nên \(\widehat {mOt} = \widehat {mOy}\) \(\left( { = {{50}^0}} \right)\) (1)
Vì Ot là tia đối của tia Ox nên \(\widehat {xOy}\) và \(\widehat {yOt}\) là hai góc kề bù
Suy ra \(\widehat {xOy} + \widehat {yOt} = {180^0}\)
\( \Rightarrow \widehat {yOt} = {180^0} - \widehat {xOt}\) \( = {180^0} - {80^0} = {100^0}\)
Trên cùng một nửa mặt phẳng bờ chứa tia Ot, có: \(\widehat {mOt} < \widehat {yOt}\) (do \({50^0} < {100^0}\)) nên tia Om nằm giữa hai tia Ot và Oy (2)
Từ (1) và (2) suy ra tia Om là tia phân giác của góc yOt.
LG bài 4
Phương pháp giải:
a) Gọi số học sinh toàn trường là \(a\). Lập luận để có \(a - 3\) là bội chung của 5, 6, 7
Sau đó kết hợp với \(a\) chia hết cho 9 và \(a < 500\) để tìm \(a.\)
b) Chứng minh và sử dụng tính chất sau:
Nếu \(\dfrac{a}{b} < 1\) thì \(\dfrac{a}{b} < \dfrac{{a + c}}{{b + c}}\).
Lời giải chi tiết:
a) Gọi số học sinh toàn trường là \(a\) học sinh \(\left( {0 < a < 500;a \in \mathbb{N}} \right)\)
Nếu toàn thể học sinh của trường xếp hàng 5, xếp hàng 6, xếp hàng 7 đều dư ra 3 bạn nên ta có \(\left( {a - 3} \right)\)chia hết cho cả 5, 6, và 7. Hay \(\left( {a - 3} \right) \in BC\left( {5;6;7} \right)\)
Ta có: \(5 = 5;6 = 2.3;\) \(7 = 7\)
Nên \(BCNN\left( {5;6;7} \right) = 5.2.3.7\) \( = 210\)
Suy ra \(BC\left( {5;6;7} \right) = B\left( {210} \right)\) \( = \left\{ {0;210;420;630;...} \right\}\)
Do đó \(\left( {a - 3} \right) \in \left\{ {0;210;420;630;...} \right\}\)
Hay \(a \in \left\{ {3;213;423;633;...} \right\}\)
Mà \(a < 500\) nên \(a \in \left\{ {3;213;423} \right\}\)
Lại có \(a\) chia hết cho 9 (do nếu toàn thể học sinh của trường xếp hàng 9 thì vừa đủ) nên \(a = 423\)
Vậy số học sinh toàn trường là 423 học sinh.
b) Ta có:
\(\begin{array}{l}P = \dfrac{{{{10}^{2018}} + 1}}{{{{10}^{2020}} + 1}} = \dfrac{{10\left( {{{10}^{2018}} + 1} \right)}}{{10\left( {{{10}^{2020}} + 1} \right)}}\\ = \dfrac{{{{10.10}^{2018}} + 10.1}}{{{{10.10}^{2020}} + 10.1}} = \dfrac{{{{10}^{2019}} + 10}}{{{{10}^{2021}} + 10}}\end{array}\)
Ta chứng minh bài tập sau:
Nếu \(\dfrac{a}{b} < 1\) thì \(\dfrac{a}{b} < \dfrac{{a + c}}{{b + c}}\).
Thật vậy, ta thấy:
\(\begin{array}{l}\dfrac{a}{b} < 1 \Rightarrow a < b\\ \Rightarrow ac < bc \Rightarrow ac + ab < bc + ab\\ \Rightarrow a\left( {b + c} \right) < b\left( {a + c} \right)\\ \Rightarrow \dfrac{a}{b} < \dfrac{{a + c}}{{b + c}}\end{array}\)
Áp dụng bài tập trên với \(a = {10^{2019}} + 1;b = {10^{2021}} + 1\).
Ta thấy, \({10^{2019}} + 1 < {10^{2021}} + 1\) nên \(\dfrac{{{{10}^{2019}} + 1}}{{{{10}^{2021}} + 1}} < 1\)
\( \Rightarrow \dfrac{{{{10}^{2019}} + 1}}{{{{10}^{2021}} + 1}} < \dfrac{{{{10}^{2019}} + 1 + 9}}{{{{10}^{2021}} + 1 + 9}}\) \( = \dfrac{{{{10}^{2019}} + 10}}{{{{10}^{2021}} + 10}}\)
\( \Rightarrow Q < P\).
Vậy \(Q < P\).
HẾT
Loigiaihay.com
- Đề thi học kì 2 môn toán lớp 6 năm 2019 - 2020 trường THCS Bình Thọ
- Giải đề thi học kì 2 toán lớp 6 năm 2020 - 2021 trường Archimeches
- Đề thi học kì 2 môn toán lớp 6 năm 2019 - 2020 trường THCS Quang Trung
- Đề thi học kì 2 môn toán lớp 6 năm 2019 - 2020 trường THCS Phan Chu Trinh
- Đề thi học kì 2 môn toán lớp 6 năm 2019 - 2020 trường THCS Giảng Võ
>> Xem thêm
Các bài khác cùng chuyên mục












Danh sách bình luận