Đề thi, đề kiểm tra Toán lớp 6 - Chân trời sáng tạo Đề thi học kì 1 Toán 6 Chân trời sáng tạo

Đề thi học kì 1 Toán 6 Chân trời sáng tạo - Đề số 17

Tải về

Tổng hợp đề thi học kì 1 lớp 6 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Khoa học tự nhiên...

Phần trắc nghiệm (2 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Đề bài

Xem đáp án

Làm đề thi

Tải về

Đề bài

I. Trắc nghiệm

Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1 :

Cho tập hợp \(A = \left\{ {x \in \mathbb{Z}| - 2 \le x < 2} \right\}\). Tập hợp A viết dưới dạng liệt kê các phần tử là:

A.

\(A = \left\{ { - 2; - 1;0;1} \right\}\).
B.

\(A = \left\{ { - 1;0;1} \right\}\).
C.

\(A = \left\{ { - 2; - 1;0} \right\}\).
D.

\(A = \left\{ { - 2; - 1;1} \right\}\).

Câu 2 :

Bội chung nhỏ nhất của 12 và 36 là:

A.

12.
B.

6.
C.

36.
D.

72.

Câu 3 :

Số đối của số 53 là:

A.

-53.
B.

-35.
C.

31.
D.

13.

Câu 4 :

Cho biết nhiệt độ của 4 hành tinh như sau:

Hành tinh có nhiệt độ thấp nhất là:

A.

Sao Hỏa.
B.

Sao Kim.
C.

Sao Thiên Vương.
D.

Sao Thủy.

Câu 5 :

Các số 2; 9; 0; -15; -4 được sắp xếp theo thứ tự giảm dần là

A.

0; 2; 9; -4; -15.
B.

9; 2; 0; -4; -15.
C.

-15; -4; 0; 2; 9.
D.

2; 9; 0; -4; -15.

Câu 6 :

Biểu đồ cột sau cho biết số quyển tập trắng được quyên góp cho học sinh khó khăn. Trong đó, số quyển tập được quyên góp của khối 6 là:

A.

200 quyển.
B.

250 quyển.
C.

150 quyển.
D.

300 quyển.

Câu 7 :

Trong các hình dưới đây, hình nào là hình thoi?

A.

Hình 1.
B.

Hình 2.
C.

Hình 3.
D.

Hình 4.

Câu 8 :

Trong các hình sau, hình nào có các góc đều bằng \(60^\circ \)?

A.

Hình chữ nhật.
B.

Hình vuông.
C.

Tam giác đều.
D.

Lục giác đều.

II. Tự luận

Câu 1 :

Thực hiện phép tính (tính hợp lí nếu có thể):

a) \( - 132 + 125\)

b) \({2^3}.\left( { - 135} \right) + {35.2^3}\)

c) \(\left[ {\left( { - 235} \right) + 171} \right] - \left( {71 - 235} \right)\)

d) \(160:\left\{ {17 + \left[ {{3^2}.5 - \left( {14 + {2^{11}}:{2^8}} \right)} \right]} \right\}\)

Câu 2 :

Tìm số nguyên \(x\), biết:

a) \(x - 10 = - 65\)

b) \(32:\left( {x + 125} \right) = - {4^2}\)

c) \(20 - 5\left( {2 - x} \right) = 45\)

Câu 3 :

Biểu đồ tranh ở hình sau cho ta thông tin về loại nhạc cụ yêu thích của các bạn học sinh khối lớp 6 của trường Trung học cơ sở A. Biết rằng không có học sinh không thích nhạc cụ.

a) Số lượng học sinh yêu thích nhạc cụ Organ nhiều hơn số học sinh yêu thích nhạc cụ trống là bao nhiêu?

b) Tính tổng số học sinh của trường Trung học cơ sở A.

Câu 4 :

Bác Khánh có mảnh vườn có hình dạng ghép bởi một hình chữ nhật và một hình thang. Kích thước của mảnh vườn được mô tả bằng bản vẽ hình sau.

a) Tính diện tích phần vườn hình chữ nhật ABCD.

b) Bác Khánh muốn mua lưới mắt cáo để rào xung quanh mảnh vườn, tính chiều dài hàng rào?

c) Qua tìm hiểu Bác Khánh thấy người ta trồng ngô thì thu được 25 nghìn đồng/m\(^2\), trồng mía thì thu được 30 nghìn đồng/m\(^2\), trồng thanh long thì thu được 40 nghìn đồng/m\(^2\). Em hãy giúp Bác Khánh chọn phương án có doanh thu tốt hơn trong hai phương án sau:

+ Phương án 1: Trồng mía trên cả mảnh vườn

+ Phương án 2: Trồng ngô trên phần mảnh vườn hình thang và trồng thanh long trên mảnh vườn hình chữ nhật.

Câu 5 :

Chứng tỏ rằng với mọi \(n \in \mathbb{N}\) thì \(2n + 1\) và \(3n + 1\) là hai số nguyên tố cùng nhau.

Lời giải và đáp án

I. Trắc nghiệm

Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1 :

Cho tập hợp \(A = \left\{ {x \in \mathbb{Z}| - 2 \le x < 2} \right\}\). Tập hợp A viết dưới dạng liệt kê các phần tử là:

A.

\(A = \left\{ { - 2; - 1;0;1} \right\}\).
B.

\(A = \left\{ { - 1;0;1} \right\}\).
C.

\(A = \left\{ { - 2; - 1;0} \right\}\).
D.

\(A = \left\{ { - 2; - 1;1} \right\}\).

Đáp án : A

Phương pháp giải :

Liệt kê các số nguyên thỏa mãn \( - 2 \le x < 2\).

Lời giải chi tiết :

Tập hợp \(A = \left\{ { - 2; - 1;0;1} \right\}\).

Đáp án A

Câu 2 :

Bội chung nhỏ nhất của 12 và 36 là:

A.

12.
B.

6.
C.

36.
D.

72.

Đáp án : C

Phương pháp giải :

Kiểm tra 36 chia hết cho 12.

Lời giải chi tiết :

Vì 36 chia hết cho 12 nên bội chung nhỏ nhất của 12 và 36 là 36.

Đáp án C

Câu 3 :

Số đối của số 53 là:

A.

-53.
B.

-35.
C.

31.
D.

13.

Đáp án : A

Phương pháp giải :

Số đối của a là –a.

Lời giải chi tiết :

Số đối của 53 là -53.

Đáp án A

Câu 4 :

Cho biết nhiệt độ của 4 hành tinh như sau:

Hành tinh có nhiệt độ thấp nhất là:

A.

Sao Hỏa.
B.

Sao Kim.
C.

Sao Thiên Vương.
D.

Sao Thủy.

Đáp án : C

Phương pháp giải :

So sánh các số nguyên âm:

Nếu a và b là các số nguyên dương và a > b thì –a < -b.

Lời giải chi tiết :

Vì 87 < 184 < 220 < 224 nên -87 > -184 > -220 > -224.

Vậy hành tinh có nhiệt độ thấp nhất là Sao Thiên Vương (\( - 224^\circ C\)).

Đáp án C

Câu 5 :

Các số 2; 9; 0; -15; -4 được sắp xếp theo thứ tự giảm dần là

A.

0; 2; 9; -4; -15.
B.

9; 2; 0; -4; -15.
C.

-15; -4; 0; 2; 9.
D.

2; 9; 0; -4; -15.

Đáp án : B

Phương pháp giải :

Chia làm 2 nhóm: các số nguyên dương và nguyên âm để so sánh.

Lời giải chi tiết :

Ta chia các số thành hai nhóm:

+ Nhóm 1: 2; 9. Ta có: 2 < 9.

+ Nhóm 2: -15; -4. Ta có: 4 < 15 nên -4 > -15.

Vậy các số sắp xếp theo thứ tự giảm dần là 9; 2; 0; -4; -15.

Đáp án B

Câu 6 :

Biểu đồ cột sau cho biết số quyển tập trắng được quyên góp cho học sinh khó khăn. Trong đó, số quyển tập được quyên góp của khối 6 là:

A.

200 quyển.
B.

250 quyển.
C.

150 quyển.
D.

300 quyển.

Đáp án : A

Phương pháp giải :

Quan sát cột khối 6.

Lời giải chi tiết :

Số quyển tập quyên góp của khối 6 là 200 quyển.

Đáp án A

Câu 7 :

Trong các hình dưới đây, hình nào là hình thoi?

A.

Hình 1.
B.

Hình 2.
C.

Hình 3.
D.

Hình 4.

Đáp án : C

Phương pháp giải :

Hình thoi là hình có 4 cạnh bằng nhau.

Lời giải chi tiết :

Hình 3 là hình thoi.

Đáp án C

Câu 8 :

Trong các hình sau, hình nào có các góc đều bằng \(60^\circ \)?

A.

Hình chữ nhật.
B.

Hình vuông.
C.

Tam giác đều.
D.

Lục giác đều.

Đáp án : C

Phương pháp giải :

Lời giải chi tiết :

Hình có các góc đều bằng \(60^\circ \) là tam giác đều.

Đáp án C

II. Tự luận

Câu 1 :

Thực hiện phép tính (tính hợp lí nếu có thể):

a) \( - 132 + 125\)

b) \({2^3}.\left( { - 135} \right) + {35.2^3}\)

c) \(\left[ {\left( { - 235} \right) + 171} \right] - \left( {71 - 235} \right)\)

d) \(160:\left\{ {17 + \left[ {{3^2}.5 - \left( {14 + {2^{11}}:{2^8}} \right)} \right]} \right\}\)

Phương pháp giải :

a) Sử dụng quy tắc cộng hai số nguyên khác dấu.

Để cộng hai số nguyên khác dấu, ta làm như sau:

Bước 1: Bỏ dấu “-” trước số nguyên âm, giữ nguyên số còn lại.

Bước 2. Trong hai số nguyên dương nhận được ở Bước 1, ta lấy số lớn hơn trừ đi số nhỏ hơn.

Bước 3. Cho hiệu vừa nhận được dấu ban đầu của số lớn hơn ở Bước 2, ta có tổng cần tìm.

b) Tính lũy thừa, áp dụng tính chất phân phối của phép nhân với phép cộng để tính.

c) Phá ngoặc sau đó sử dụng tính chất của kết hợp của phép cộng để nhóm.

d) Sử dụng các quy tắc tính với số nguyên và thứ tự thực hiện phép tính:

Nếu biểu thức có các dấu ngoặc: ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính theo thứ tự:

( ) → [ ] → { }

Lời giải chi tiết :

a) \( - 132 + 125\)\( = - \left( {132 - 125} \right) = - 7\)

b) \({2^3}.\left( { - 135} \right) + {35.2^3}\)

\(\begin{array}{l} = 8.\left( { - 135} \right) + 35.8\\ = 8\left( { - 135 + 35} \right)\\ = 8.\left( { - 100} \right)\\ = - 800\end{array}\)

c) \(\left[ {\left( { - 235} \right) + 171} \right] - \left( {71 - 235} \right)\)

\(\begin{array}{l} = - 235 + 171 - 71 - 235\\ = \left( { - 235 + 235} \right) + \left( {171 - 71} \right)\\ = 0 + 100\\ = 100\end{array}\)

d) \(160:\left\{ {17 + \left[ {{3^2}.5 - \left( {14 + {2^{11}}:{2^8}} \right)} \right]} \right\}\)

\(\begin{array}{l} = 160:\{ 17 + [{3^2}.5 - (14 + {2^3})]\} \\ = 160:\left\{ {17 + \left[ {9.5 - \left( {14 + 8} \right)} \right]} \right\}\\ = 160:\left\{ {17 + \left[ {45 - 22} \right]} \right\}\\ = 160:\left\{ {17 + 23} \right\}\\ = 160:40\\ = 4\end{array}\)

Câu 2 :

Tìm số nguyên \(x\), biết:

a) \(x - 10 = - 65\)

b) \(32:\left( {x + 125} \right) = - {4^2}\)

c) \(20 - 5\left( {2 - x} \right) = 45\)

Phương pháp giải :

a) Muốn tìm một số hạng trong một tổng ta lấy tổng trừ đi số hạng còn lại.

b) Áp dụng quy tắc chuyển vế để tìm x.

c) Áp dụng quy tắc chuyển vế để tìm x.

Lời giải chi tiết :

a) \(x - 10 = - 65\)

\(\begin{array}{l}x = - 65 + 10\\x = - 55\end{array}\)

Vậy \(x = - 55\)

b) \(32:\left( {x + 125} \right) = - {4^2}\)

\(\begin{array}{l}32:\left( {x + 125} \right) = - 16\\x + 125 = 32:\left( { - 16} \right)\\x + 125 = - 2\\x = - 2 - 125\\x = - 127\end{array}\)

Vậy \(x = - 127\)

c) \(20 - 5\left( {2 - x} \right) = 45\)

\(\begin{array}{l}5\left( {2 - x} \right) = 20 - 45\\5\left( {2 - x} \right) = - 25\\2 - x = - 25:5\\2 - x = - 5\\x = 2 - \left( { - 5} \right)\\x = 7\end{array}\)

Vậy \(x = 7\).

Câu 3 :

a) Số lượng học sinh yêu thích nhạc cụ Organ nhiều hơn số học sinh yêu thích nhạc cụ trống là bao nhiêu?

b) Tính tổng số học sinh của trường Trung học cơ sở A.

Phương pháp giải :

a) Tính số học sinh yêu thích nhạc cụ Organ, nhạc cụ trống.

b) Tính số học sinh yêu thích kèn, ghi ta, sáo. Tổng số học sinh = số học sinh yêu thích các loại nhạc cụ.

Lời giải chi tiết :

a) Số học sinh yêu thích nhạc cụ Organ là:

\(4.10 + 5.1 = 45{\mkern 1mu} (HS)\)

Số học sinh yêu thích nhạc cụ trống là:

\(4.10 = 40{\mkern 1mu} (HS)\)

Số lượng học sinh yêu thích nhạc cụ Organ nhiều hơn số học sinh yêu thích nhạc cụ trống là:

\(45 - 40 = 5{\mkern 1mu} (HS)\)

b) Số học sinh yêu thích nhạc cụ kèn là:

\(2.10 + 5.1 = 25{\mkern 1mu} (HS)\)

Số học sinh yêu thích nhạc cụ ghi ta là:

\(5.10 + 5.1 = 55{\mkern 1mu} (HS)\)

Số học sinh yêu thích nhạc cụ sáo là:

\(3.10 + 5.1 = 35{\mkern 1mu} (HS)\)

Tổng số học sinh của trường Trung học cơ sở A là:

\(45 + 40 + 25 + 55 + 35 = 200{\mkern 1mu} (HS)\)

Câu 4 :

Bác Khánh có mảnh vườn có hình dạng ghép bởi một hình chữ nhật và một hình thang. Kích thước của mảnh vườn được mô tả bằng bản vẽ hình sau.

a) Tính diện tích phần vườn hình chữ nhật ABCD.

b) Bác Khánh muốn mua lưới mắt cáo để rào xung quanh mảnh vườn, tính chiều dài hàng rào?

+ Phương án 1: Trồng mía trên cả mảnh vườn

+ Phương án 2: Trồng ngô trên phần mảnh vườn hình thang và trồng thanh long trên mảnh vườn hình chữ nhật.

Phương pháp giải :

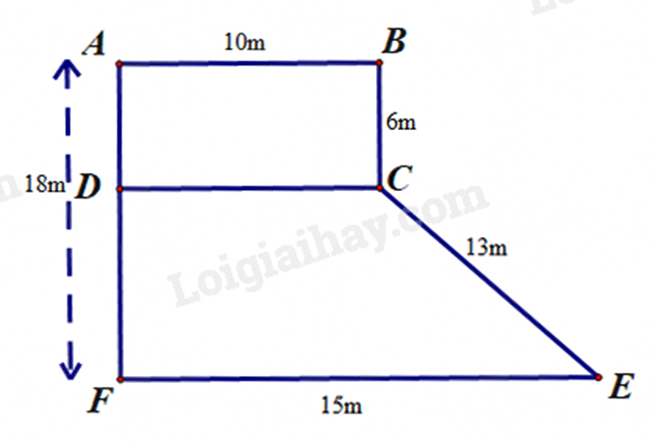
a) Áp dụng công thức tính diện tích phần vườn hình chữ nhật = chiều dài . chiều rộng.

b) Tính chu vi của mảnh vườn. Chiều dài hàng rào chính là chu vi của mảnh vườn.

c) Tính diện tích phần vườn hình thang = tổng hai đáy . chiều cao : 2.

Tính diện tích vườn bằng tổng diện tích phần vườn hình chữ nhật và phần vườn hình thang.

Phương án 1. Tính doanh thu khi trồng mía trên cả mảnh vườn.

Phương án 2. Tính doanh thu trồng ngô + doanh thu trồng thanh long.

Doanh thu = diện tích . số tiền thu được trên 1 mét vuông.

Lời giải chi tiết :

a) Diện tích phần vườn hình chữ nhật là: \(10.6 = 60\left( {{m^2}} \right)\)

b) Chiều dài hàng rào là: \(10 + 6 + 13 + 15 + 18 = 62\left( m \right)\)

c) Chiều cao phần vườn hình thang là: \(18 - 6 = 12\left( m \right)\)

Diện tích phần vườn hình thang là: \(\left( {10 + 15} \right).12:2 = 150\left( {{m^2}} \right)\)

Tổng diện tích mảnh vườn là: \(60 + 150 = 210\left( {{m^2}} \right)\)

- Doanh thu theo phương án 1 là: \(210.30 = 6300\) (nghìn đồng)

- Doanh thu theo phương án 2 là: \(25.150 + 40.60 = 6150\) (nghìn đồng)

Vậy bác Khánh chọn phương án 1 sẽ có doanh thu tốt hơn.

Câu 5 :

Chứng tỏ rằng với mọi \(n \in \mathbb{N}\) thì \(2n + 1\) và \(3n + 1\) là hai số nguyên tố cùng nhau.

Phương pháp giải :

Hai số nguyên tố cùng nhau nếu ước chung lớn nhất của chúng bằng 1.

Giả sử ƯCLN(2n+1;3n+1) = d (d \( \in \mathbb{N}\)).

Chứng minh d = 1 nên \(2n + 1\) và \(3n + 1\) là hai số nguyên tố cùng nhau.

Lời giải chi tiết :

Gọi ƯCLN(2n+1;3n+1) = d (d \( \in \mathbb{N}\)).

Suy ra \(2n + 1 \vdots d\); \(3n + 1 \vdots d\).

Do đó \(3\left( {2n + 1} \right) \vdots d\); \(2\left( {3n + 1} \right) \vdots d\)

hay \(6n + 3 \vdots d\); \(6n + 2 \vdots d\)

Suy ra \(\left( {6n + 3} \right) - \left( {6n + 2} \right) \vdots d\) hay \(1 \vdots d\) suy ra d \( \in \) Ư(1) = {1; -1}

Mà \(d \in \mathbb{N}\) nên d = 1.

Do đó ƯCLN(2n+1;3n+1) = 1

Vậy \(2n + 1\) và \(3n + 1\) là hai số nguyên tố cùng nhau.

Đề thi học kì 1 Toán 6 Chân trời sáng tạo - Đề số 18

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Xem chi tiết

Đề thi học kì 1 Toán 6 Chân trời sáng tạo - Đề số 16

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 15 - Chân trời sáng tạo

Phần trắc nghiệm (3 điểm) Câu 1: Tập hợp các số tự nhiên khác 0 không vượt quá 4 là :

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 14 - Chân trời sáng tạo

Phần trắc nghiệm (3 điểm) Câu 1: Cho hình bình hành ABCD có AB = 5 cm, BC = 8 cm thì:

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 13 - Chân trời sáng tạo

Phần trắc nghiệm (3 điểm) Câu 1: Cho tập hợp A = {1; 3; 9; 0; 4; 2}, số phần tử trong tập hợp A là:

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 12 - Chân trời sáng tạo

Phần trắc nghiệm (3 điểm) Câu 1: Cho tập hợp M = {x ∈ N| 15 < x ≤ 20}. Hãy chọn khẳng định đúng:

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 11 - Chân trời sáng tạo

Phần trắc nghiệm (3 điểm) Câu 1: Tập hợp số tự nhiên được kí hiệu là:

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 10 - Chân trời sáng tạo

Phần I: Trắc nghiệm (5 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 9 - Chân trời sáng tạo

Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 8 - Chân trời sáng tạo

Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết

Đề thi học kì 1 Toán 6 - Đề số 7 - Chân trời sáng tạo