-
Đề khảo sát chất lượng đầu năm
-
Đề thi giữa kì 1
- Đề thi giữa kì 1 - Đề số 1
- Đề thi giữa kì 1 - Đề số 2
- Đề thi giữa kì 1 - Đề số 3
- Đề thi giữa kì 1 - Đề số 4
- Đề thi giữa kì 1 - Đề số 5
- Đề thi giữa kì 1 - Đề số 6
- Đề thi giữa kì 1 - Đề số 6
- Đề thi giữa kì 1 - Đề số 7
- Đề thi giữa kì 1 - Đề số 8
- Đề thi giữa kì 1 - Đề số 9
- Đề thi giữa kì 1 - Đề số 10
- Đề thi giữa kì 1 - Đề số 11
- Đề thi giữa kì 1 - Đề số 12
- Đề thi giữa kì 1 - Đề số 13
- Đề thi giữa kì 1 - Đề số 14
- Đề thi giữa kì 1 - Đề số 15
-
Đề thi học kì 1
- Đề cương ôn tập học kì 1
- Đề thi học kì 1 Toán 10 - Đề số 1
- Đề thi học kì 1 Toán 10 - Đề số 2
- Đề thi học kì 1 Toán 10 - Đề số 3
- Đề thi học kì 1 Toán 10 - Đề số 4
- Đề thi học kì 1 Toán 10 - Đề số 5
- Đề thi học kì 1 Toán 10 - Đề số 6
- Đề thi học kì 1 Toán 10 - Đề số 7
- Đề thi học kì 1 Toán 10 - Đề số 8
- Đề thi học kì 1 Toán 10 - Đề số 9
- Đề thi học kì 1 Toán 10 - Đề số 10
- Đề thi học kì 1 Toán 10 - Đề số 11
- Đề thi học kì 1 Toán 10 - Đề số 12
- Đề thi học kì 1 Toán 10 - Đề số 13
-
Đề thi giữa kì 2
-
Đề thi học kì 2
Đề thi giữa kì 1 Toán 10 - Đề số 14
Tổng hợp đề thi giữa kì 1 lớp 10 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Đề thi giữa kì 1 Toán 10 - Đề số 14
Đề bài
Mô tả tập hợp \(A = \{ x \in \mathbb{Z}| - 1 \le x < 2\} \) bằng cách liệt kê:
-
A.
\(A = \{ - 1;0;1;2\} \)
-
B.
\(A = \{ 0;1\} \)
-
C.
\(A = \{ - 1;0;1; - 1\} \)
-
D.
\(A = \{ - 1;0;1\} \)
Cho tam giác ABC có AB = c, AC = b, CB = a, R là bán kính đường tròn ngoại tiếp. Hệ thức nào sau đây là sai?
-
A.
\(\frac{a}{{\sin A}} = 2R\)
-
B.
\(\sin A = \frac{a}{{2R}}\)
-
C.
\(b\sin B = 2R\)
-
D.
\(\sin C = \frac{{c\sin A}}{a}\)
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
-
A.
\(3x + 4y - 5 \le 0\)
-
B.
\(3x + {y^2} - 5 \le 0\)
-
C.
\({x^2} + y + 3 \le 0\)
-
D.
\(2xy - 5 \ge 0\)
Cho tam giác ABC có ba cạnh a = BC, b = AC, c = AB. Khi đó
-
A.
\({a^2} = {b^2} + {c^2} + 2bc\cos \widehat {BAC}\)
-
B.
\({a^2} = {b^2} + {c^2} - 2bc\sin \widehat {BAC}\)
-
C.
\({a^2} = {b^2} + {c^2} + 2bc\sin \widehat {BAC}\)
-
D.
\({a^2} = {b^2} + {c^2} - 2bc\cos \widehat {BAC}\)
Trong các đẳng thức sau, đẳng thức nào đúng?
-
A.
\(\sin ({90^o} - \alpha ) = - \cos \alpha \)
-
B.
\(\sin ({90^o} - \alpha ) = - \sin \alpha \)
-
C.
\(\sin ({90^o} - \alpha ) = \cos \alpha \)
-
D.
\(\sin ({90^o} - \alpha ) = \sin \alpha \)
Cặp số (-2;3) là nghiệm của bất phương trình nào dưới đây?
-
A.
2x + y + 1 > 0
-
B.
x + 3y + 1 < 0
-
C.
2x – y – 1 \( \ge \) 0
-
D.
x + y + 1 > 0
Phủ định của mệnh đề “\(\exists x \in \mathbb{R},{x^2} - x + 1 < 0\)” là mệnh đề
-
A.
“\(\forall x \in \mathbb{R},{x^2} - x + 1 \ge 0\)”
-
B.
“\(\forall x \in \mathbb{R},{x^2} - x + 1 < 0\)”
-
C.
“\(\forall x \in \mathbb{R},{x^2} - x + 1 > 0\)”
-
D.
“\(\exists x \in \mathbb{R},{x^2} - x + 1 \ge 0\)”
Nửa mặt phẳng không tô đậm (bao gồm cả đường thẳng $d$) ở hình dưới đây là miền nghiệm của bất phương trình nào trong các bất phương trình sau?
-
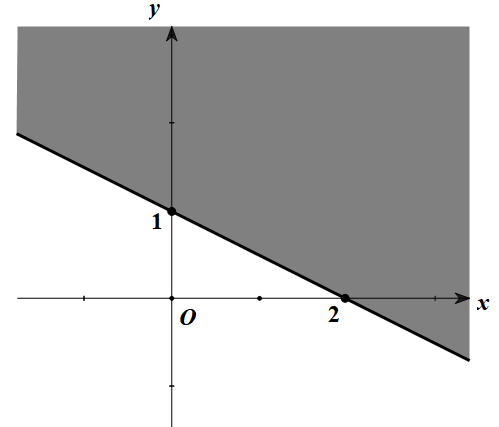
A.
$2x + y \geq 2$.
-
B.
$x + 2y \geq 2$.
-
C.
$2x + y \leq 2$.
-
D.
$x + 2y \leq 2$.
Có bao nhiêu phát biểu dưới đây là mệnh đề?
1) “17 là số nguyên tố”.
2) “Tam giác vuông có một đường trung tuyến bằng một nửa cạnh huyền".
3) "Các em hãy cố gắng học tập thật tốt nhé"!
4) "Mọi hình chữ nhật đều nội tiếp được đường tròn".
-
A.
4
-
B.
3
-
C.
2
-
D.
1
Tâp hợp \(\left[ {0;4} \right] \cap \left[ {3;5} \right] \) là
-
A.
\(\emptyset \)
-
B.
\(\left[ {0;5} \right]\)
-
C.
\(\left[ {3;4} \right]\)
-
D.
\(\left\{ {3;4} \right\}\)
Cho tập hợp \(A = \{ 1;2;3;4\} \). Tập hợp nào sau đây là tập con của A?
-
A.
\(\{ 1;3\} \)
-
B.
\(\{ 2;5\} \)
-
C.
\(\{ 0;3\} \)
-
D.
\(\{ 0;1;2\} \)
Cho mệnh đề chứa biến P(x): \(x + 2 > {x^2}\). Mệnh đề nào sau đây đúng?
-
A.
P(3)
-
B.
P(-1)
-
C.
P(1)
-
D.
P(5)
Cho hệ bất phương trình sau: $\left\{ \begin{array}{l} {x - 2y \leq 0} \\ {5x - y \geq - 4} \\ {x + 2y \leq 5} \end{array} \right.$ và biểu thức $F = 3x + 5y$. Các mệnh đề sau đúng hay sai?
a) Điểm $B\left( {\dfrac{5}{2};\dfrac{5}{4}} \right)$ là điểm thuộc miền nghiệm của hệ bất phương trình thỏa mãn $F = 3x + 5y$đạt giá trị lớn nhất.
b) Miền nghiệm của hệ bất phương trình $\left\{ \begin{array}{l} {x - 2y \leq 0} \\ {5x - y \geq - 4} \\ {x + 2y \leq 5} \end{array} \right.$ là miền tam giác.
c) Miền nghiệm của bất phương trình $5x - y \geq - 4$ là nửa mặt phẳng bờ là $d:5x - y = - 4$và chứa gốc tọa độ O, kể cả bờ.
d) Điểm $M\left( {1;2024} \right)$ thỏa mãn miền nghiệm của hệ bất phương trình.
Cho tam giác $ABC$ có $BC = 12\text{cm}$, góc $\widehat{B} = 15{^\circ}$, $\widehat{C} = 30{^\circ}$. Các mệnh đề sau đúng hay sai?
a) $AB = 6\sqrt{2}$.
b) Độ dài đường cao $AH = \dfrac{23}{11}$.
c) Bán kính đường tròn nội tiếp tam giác ABC là $2,6$.
d) $R = \dfrac{a}{\sin A}$.
Tính diện tích một lá cờ hình tam giác cân có độ dài cạnh bên là 90 cm và góc ở đỉnh là \({35^o}\) (đơn vị: \(c{m^2}\), làm tròn kết quả đến hàng đơn vị).
Trong một cuộc thi về “bữa ăn dinh dưỡng”, ban tổ chức yêu cầu đề bảo đảm lượng dinh dưỡng hàng ngày thì mỗi gia đình có 4 thành viên cần ít nhất 900 đơn vị prôtêin và 400 đơn vị lipit trong thức ăn hằng ngày. Mỗi kg thịt bò chứa 800 đơn vị prôtêin và 200 đơn vị lipit, 1 kg thịt heo chứa 600 đơn vị prôtêin và 400 đơn vị lipit. Biết rằng người nội trợ chỉ được chi tối đa 200 nghìn đồng để mua thịt. Biết rằng 1 kg thịt bò giá 200 nghìn đồng, 1 kg thịt heo giá 100 nghìn đồng. Người nội trợ nên mua x (kg) thịt bò và y (kg) thịt heo để chi thấp nhất cho khẩu phần thức ăn mà vẫn đảm bảo chất dinh dưỡng, khi đó hãy tìm x + 2y.
Từ hai vị trí $A$ và $B$ của một tòa nhà, người ta quan sát đỉnh $C$ của ngọn núi. Biết rằng độ cao $AB = 70$ m, phương nhìn $AC$ tạo với phương nằm ngang góc $30^{{^\circ}}$, phương nhìn $BC$ tạo với phương nằm ngang góc $15^{{^\circ}}30'$. Ngọn núi đó có độ cao so với mặt đất là bao nhiêu mét? (làm tròn đến hàng đơn vị).
Cho số thực $m < 0$ và hai tập hợp $A = ( - \infty;4m),B = \left( {\dfrac{25}{m}; + \infty} \right)$. Số các giá trị nguyên của tham số $m$ để $A \cap B \neq \varnothing$?
Lời giải và đáp án
Mô tả tập hợp \(A = \{ x \in \mathbb{Z}| - 1 \le x < 2\} \) bằng cách liệt kê:
-
A.
\(A = \{ - 1;0;1;2\} \)
-
B.
\(A = \{ 0;1\} \)
-
C.
\(A = \{ - 1;0;1; - 1\} \)
-
D.
\(A = \{ - 1;0;1\} \)
Đáp án : D
Liệt kê từng phần tử thỏa mãn.
\(A = \{ x \in \mathbb{Z}| - 1 \le x < 2\} = \{ - 1;0;1\} \).
Mỗi phần tử chỉ liệt kê đúng một lần.
Cho tam giác ABC có AB = c, AC = b, CB = a, R là bán kính đường tròn ngoại tiếp. Hệ thức nào sau đây là sai?
-
A.
\(\frac{a}{{\sin A}} = 2R\)
-
B.
\(\sin A = \frac{a}{{2R}}\)
-
C.
\(b\sin B = 2R\)
-
D.
\(\sin C = \frac{{c\sin A}}{a}\)
Đáp án : C
Sử dụng định lí sin trong tam giác ABC.
Theo định lí sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\).
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
-
A.
\(3x + 4y - 5 \le 0\)
-
B.
\(3x + {y^2} - 5 \le 0\)
-
C.
\({x^2} + y + 3 \le 0\)
-
D.
\(2xy - 5 \ge 0\)
Đáp án : A
Quan sát dạng (ẩn, bậc) của bất phương trình.
Các bất phương trình ở đáp án B, C, D đều là bất phương trình bậc hai hai ẩn.
Cho tam giác ABC có ba cạnh a = BC, b = AC, c = AB. Khi đó
-
A.
\({a^2} = {b^2} + {c^2} + 2bc\cos \widehat {BAC}\)
-
B.
\({a^2} = {b^2} + {c^2} - 2bc\sin \widehat {BAC}\)
-
C.
\({a^2} = {b^2} + {c^2} + 2bc\sin \widehat {BAC}\)
-
D.
\({a^2} = {b^2} + {c^2} - 2bc\cos \widehat {BAC}\)
Đáp án : D
Dựa vào định lí cosin trong tam giác.
Cho tam giác ABC có ba cạnh a = BC, b = AC, c = AB. Khi đó \({a^2} = {b^2} + {c^2} - 2bc\cos \widehat {BAC}\).
Trong các đẳng thức sau, đẳng thức nào đúng?
-
A.
\(\sin ({90^o} - \alpha ) = - \cos \alpha \)
-
B.
\(\sin ({90^o} - \alpha ) = - \sin \alpha \)
-
C.
\(\sin ({90^o} - \alpha ) = \cos \alpha \)
-
D.
\(\sin ({90^o} - \alpha ) = \sin \alpha \)
Đáp án : C
Dựa vào mối quan hệ giữa các giá trị lượng giác của hai góc phụ nhau.
Với hai góc phụ nhau \(\alpha \) và \({90^o} - \alpha \), ta có \(\sin ({90^o} - \alpha ) = \cos \alpha \).
Cặp số (-2;3) là nghiệm của bất phương trình nào dưới đây?
-
A.
2x + y + 1 > 0
-
B.
x + 3y + 1 < 0
-
C.
2x – y – 1 \( \ge \) 0
-
D.
x + y + 1 > 0
Đáp án : D
Thay cặp số vào từng bất phương trình, nếu thỏa mãn thì là nghiệm của bất phương trình đó.
Xét A: 2.(-2) + 3 + 1 > 0 sai nên (-2;3) không là nghiệm của 2x + y + 1 > 0.
Xét B: -2 + 3.3 + 1 < 0 sai nên (-2;3) không là nghiệm của x + 3y + 1 < 0.
Xét C: 2.(-2) – 3 – 1 \( \ge \) 0 sai nên (-2;3) không là nghiệm của 2x – y – 1 \( \ge \) 0.
Xét D: -2 + 3 + 1 > 0 đúng nên (-2;3) là nghiệm của x + y + 1 > 0.
Phủ định của mệnh đề “\(\exists x \in \mathbb{R},{x^2} - x + 1 < 0\)” là mệnh đề
-
A.
“\(\forall x \in \mathbb{R},{x^2} - x + 1 \ge 0\)”
-
B.
“\(\forall x \in \mathbb{R},{x^2} - x + 1 < 0\)”
-
C.
“\(\forall x \in \mathbb{R},{x^2} - x + 1 > 0\)”
-
D.
“\(\exists x \in \mathbb{R},{x^2} - x + 1 \ge 0\)”
Đáp án : A
Phủ định của “\(\forall \)” là “\(\exists \)”.
Phủ định của “\( < \)” là “\( \ge \)”.
Mệnh đề phủ định của mệnh đề trên là “\(\forall x \in \mathbb{R},{x^2} - x + 1 \ge 0\)”.
Nửa mặt phẳng không tô đậm (bao gồm cả đường thẳng $d$) ở hình dưới đây là miền nghiệm của bất phương trình nào trong các bất phương trình sau?
-
A.
$2x + y \geq 2$.
-
B.
$x + 2y \geq 2$.
-
C.
$2x + y \leq 2$.
-
D.
$x + 2y \leq 2$.
Đáp án : D
Lập phương trình đường thẳng bờ của miền nghiệm dựa vào các điểm thuộc đường thẳng.
Vì điểm O(0;0) thuộc miền nghiệm nên ta suy ra chiều của bất phương trình.
Giả sử đường thẳng bờ của miền nghiệm có dạng y = ax + b.
Đường thẳng đi qua điểm (2;0) và (0;1) nên ta có:
\(\left\{ \begin{array}{l}0 = 2a + b\\1 = 0a + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{1}{2}\\b = 1\end{array} \right. \Rightarrow y = - \frac{1}{2}x + 1 \Leftrightarrow x + 2y = 2\).
Do đó ta loại đáp án A, C.
Vì O(0;0) thuộc miền nghiệm của bất phương trình nên:
\(0 + 2.0 = 0 \le 2\).
Vậy bất phương trình là \(x + 2y \le 2\).
Có bao nhiêu phát biểu dưới đây là mệnh đề?
1) “17 là số nguyên tố”.
2) “Tam giác vuông có một đường trung tuyến bằng một nửa cạnh huyền".
3) "Các em hãy cố gắng học tập thật tốt nhé"!
4) "Mọi hình chữ nhật đều nội tiếp được đường tròn".
-
A.
4
-
B.
3
-
C.
2
-
D.
1
Đáp án : B
Mệnh đề là một khẳng định có tính đúng sai.
Chỉ có câu 3) không phải mệnh đề.
Tâp hợp \(\left[ {0;4} \right] \cap \left[ {3;5} \right] \) là
-
A.
\(\emptyset \)
-
B.
\(\left[ {0;5} \right]\)
-
C.
\(\left[ {3;4} \right]\)
-
D.
\(\left\{ {3;4} \right\}\)
Đáp án : C
Giao hai tập hợp là tập hợp gồm các phần tử thuộc cả hai tập hợp.
Tập \(\left[ {0;4} \right] \):
Tập \(\left[ {0;4} \right] \cap \left[ {3;5} \right] \):
Vậy \(\left[ {0;4} \right] \cap \left[ {3;5} \right] = \left[ {3;4} \right]\).
Học sinh có thể vẽ hình để dễ hình dung:
Cho tập hợp \(A = \{ 1;2;3;4\} \). Tập hợp nào sau đây là tập con của A?
-
A.
\(\{ 1;3\} \)
-
B.
\(\{ 2;5\} \)
-
C.
\(\{ 0;3\} \)
-
D.
\(\{ 0;1;2\} \)
Đáp án : A
Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập hợp con của B.
Ta có:
\(\{ 1;3\} \subset \{ 1;2;3;4\} = A\). Chọn A.
\(\{ 2;5\} \not{ \subset }\{ 1;2;3;4\} = A\). Loại B.
\(\{ 0;3\} \not{ \subset }\{ 1;2;3;4\} = A\). Loại C.
\(\{ 0;1;2\} \not{ \subset }\{ 1;2;3;4\} = A\). Loại D.
Cho mệnh đề chứa biến P(x): \(x + 2 > {x^2}\). Mệnh đề nào sau đây đúng?
-
A.
P(3)
-
B.
P(-1)
-
C.
P(1)
-
D.
P(5)
Đáp án : C
Xét từng mệnh đề.
Ta có:
P(3): \(3 + 2 > {3^2}\) là mệnh đề sai. Loại A.
P(-1): \( - 1 + 2 > {( - 1)^2}\) là mệnh đề sai. Loại B.
P(1): \(1 + 2 > {1^2}\) là mệnh đề đúng. Chọn C.
P(3): \(5 + 2 > {5^2}\) là mệnh đề sai. Loại D.
Cho hệ bất phương trình sau: $\left\{ \begin{array}{l} {x - 2y \leq 0} \\ {5x - y \geq - 4} \\ {x + 2y \leq 5} \end{array} \right.$ và biểu thức $F = 3x + 5y$. Các mệnh đề sau đúng hay sai?
a) Điểm $B\left( {\dfrac{5}{2};\dfrac{5}{4}} \right)$ là điểm thuộc miền nghiệm của hệ bất phương trình thỏa mãn $F = 3x + 5y$đạt giá trị lớn nhất.
b) Miền nghiệm của hệ bất phương trình $\left\{ \begin{array}{l} {x - 2y \leq 0} \\ {5x - y \geq - 4} \\ {x + 2y \leq 5} \end{array} \right.$ là miền tam giác.
c) Miền nghiệm của bất phương trình $5x - y \geq - 4$ là nửa mặt phẳng bờ là $d:5x - y = - 4$và chứa gốc tọa độ O, kể cả bờ.
d) Điểm $M\left( {1;2024} \right)$ thỏa mãn miền nghiệm của hệ bất phương trình.
a) Điểm $B\left( {\dfrac{5}{2};\dfrac{5}{4}} \right)$ là điểm thuộc miền nghiệm của hệ bất phương trình thỏa mãn $F = 3x + 5y$đạt giá trị lớn nhất.
b) Miền nghiệm của hệ bất phương trình $\left\{ \begin{array}{l} {x - 2y \leq 0} \\ {5x - y \geq - 4} \\ {x + 2y \leq 5} \end{array} \right.$ là miền tam giác.
c) Miền nghiệm của bất phương trình $5x - y \geq - 4$ là nửa mặt phẳng bờ là $d:5x - y = - 4$và chứa gốc tọa độ O, kể cả bờ.
d) Điểm $M\left( {1;2024} \right)$ thỏa mãn miền nghiệm của hệ bất phương trình.
Áp dụng quy tắc tính xác định miền nghiệm của hệ bất phương trình bậc nhất hai ẩn.
a) Đúng. Miền nghiệm của hệ bất phương trình là miền tam giác ABC với \(A\left( { - \frac{3}{{11}};\frac{{29}}{{11}}} \right)\), \(B\left( {\frac{5}{2};\frac{5}{4}} \right)\), \(C\left( { - \frac{8}{9}; - \frac{4}{9}} \right)\).
\(F\left( { - \frac{3}{{11}};\frac{{29}}{{11}}} \right) = 3\left( { - \frac{3}{{11}}} \right) + 5.\frac{{29}}{{11}} = \frac{{136}}{{11}}\);
\(F\left( { - \frac{8}{9}; - \frac{4}{9}} \right) = 3\left( { - \frac{8}{9}} \right) + 5.\left( { - \frac{4}{9}} \right) = - \frac{{44}}{9}\);
\(F\left( {\frac{5}{2};\frac{5}{4}} \right) = 3.\frac{5}{2} + 5.\frac{5}{4} = \frac{{55}}{4}\).
Ta có \(F\left( {\frac{5}{2};\frac{5}{4}} \right) = \frac{{55}}{4}\) lớn nhất trong các giá trị trên, do đó điểm $B\left( {\dfrac{5}{2};\dfrac{5}{4}} \right)$ là điểm thuộc miền nghiệm của hệ bất phương trình thỏa mãn $F = 3x + 5y$đạt giá trị lớn nhất.
b) Đúng. Miền nghiệm của hệ là miền tam giác giới hạn bởi ba đường thẳng \(x - 2y = 0\), \(5x - y = - 4\), \(x + 2y = 5\).
c) Đúng. Ta có \(5.0 - 0 = 0 \ge - 4\) nên O(0;0) thuộc miền nghiệm của bất phương trình.
Vậy miền nghiệm của bất phương trình $5x - y \geq - 4$ là nửa mặt phẳng bờ là $d:5x - y = - 4$và chứa gốc tọa độ O, kể cả bờ.
d) Sai. Vì \(1 + 2.2024 > 5\) nên tọa độ điểm M không thỏa mãn phương trình thứ ba của hệ. Do đó điểm M không thỏa mãn miền nghiệm của hệ bất phương trình.
Cho tam giác $ABC$ có $BC = 12\text{cm}$, góc $\widehat{B} = 15{^\circ}$, $\widehat{C} = 30{^\circ}$. Các mệnh đề sau đúng hay sai?
a) $AB = 6\sqrt{2}$.
b) Độ dài đường cao $AH = \dfrac{23}{11}$.
c) Bán kính đường tròn nội tiếp tam giác ABC là $2,6$.
d) $R = \dfrac{a}{\sin A}$.
a) $AB = 6\sqrt{2}$.
b) Độ dài đường cao $AH = \dfrac{23}{11}$.
c) Bán kính đường tròn nội tiếp tam giác ABC là $2,6$.
d) $R = \dfrac{a}{\sin A}$.
Áp dụng định lí cosin, các công thức tính diện tích tam giác.
\(\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {15^o} - {30^o} = {135^o}\).
a) Đúng. \(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}} \Leftrightarrow AB = \frac{{BC.\sin C}}{{\sin A}} = \frac{{12.\sin {{30}^o}}}{{\sin {{135}^o}}} = 6\sqrt 2 \).
b) Sai. \(S = \frac{1}{2}AB.BC\sin B = \frac{1}{2}AH.BC\)
\( \Leftrightarrow AB\sin B = AH \Leftrightarrow AH = 6\sqrt 2 .\sin {15^o} = - 3 + 3\sqrt 3 \).
c) Sai. \(S = \frac{1}{2}AH.BC = \frac{1}{2}\left( { - 3 + 3\sqrt 3 } \right).12 = - 18 + 18\sqrt 3 \).
\(\frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}} \Leftrightarrow AC = \frac{{BC.\sin B}}{{\sin A}} = \frac{{12.\sin {{15}^o}}}{{\sin {{135}^o}}} = - 6 + 6\sqrt 3 \).
\(p = \frac{{AB + BC + AC}}{2} = \frac{{6\sqrt 2 + 12 + \left( { - 6 + 6\sqrt 3 } \right)}}{2} = 3\left( {1 + \sqrt 2 + \sqrt 3 } \right)\).
\(r = \frac{S}{p} = \frac{{ - 18 + 18\sqrt 3 }}{{3\left( {1 + \sqrt 2 + \sqrt 3 } \right)}} \approx 1,1\).
d) Sai. \(2R = \frac{a}{{\sin A}}\).
Tính diện tích một lá cờ hình tam giác cân có độ dài cạnh bên là 90 cm và góc ở đỉnh là \({35^o}\) (đơn vị: \(c{m^2}\), làm tròn kết quả đến hàng đơn vị).
Áp dụng công thức \(S = \frac{1}{2}bc\sin A\).
Kí hiệu các điểm như hình.
Từ giả thiết, ta có AB = AC = 90 cm, \(\widehat A = {35^o}\).
Diện tích lá cờ là \(S = \frac{1}{2}AB.AC\sin A = \frac{1}{2}90.90\sin {35^o} \approx 2323\) \(\left( {c{m^2}} \right)\).
Trong một cuộc thi về “bữa ăn dinh dưỡng”, ban tổ chức yêu cầu đề bảo đảm lượng dinh dưỡng hàng ngày thì mỗi gia đình có 4 thành viên cần ít nhất 900 đơn vị prôtêin và 400 đơn vị lipit trong thức ăn hằng ngày. Mỗi kg thịt bò chứa 800 đơn vị prôtêin và 200 đơn vị lipit, 1 kg thịt heo chứa 600 đơn vị prôtêin và 400 đơn vị lipit. Biết rằng người nội trợ chỉ được chi tối đa 200 nghìn đồng để mua thịt. Biết rằng 1 kg thịt bò giá 200 nghìn đồng, 1 kg thịt heo giá 100 nghìn đồng. Người nội trợ nên mua x (kg) thịt bò và y (kg) thịt heo để chi thấp nhất cho khẩu phần thức ăn mà vẫn đảm bảo chất dinh dưỡng, khi đó hãy tìm x + 2y.
Ứng dụng hệ bất phương trình bậc nhất hai ẩn.
Người nội trợ chỉ được chi tối đa 200 nghìn đồng, do đó:
- Không thể mua nhiều hơn 1 kg thịt bò (1 kg bò = 200 nghìn đồng);
- Không thể mua nhiều hơn 2 kg thịt heo (1 kg heo = 100 nghìn đồng).
Do đó, ta có điều kiện \(0 \le x \le 1\), \(0 \le y \le 2\).
Với x (kg) thịt bò và y (kg) thịt heo:
- Chi phí để mua là f(x;y) = 200000x + 100000y, không được vượt 200 nghìn đồng.
- Lượng prorein cung cấp là g(x;y) = 800x + 600y, cần ít nhất 900 đơn vị.
- Lượng lipit cung cấp là h(x;y) = 200x + 400y, cần ít nhất 400 đơn vị.
Do đó, ta có hệ phương trình:
\(\left\{ \begin{array}{l}0 \le x \le 1\\0 \le y \le 2\\200000x + 100000y \le 200000\\800x + 600y \ge 900\\200x + 400y \ge 400\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 \le x \le 1\\0 \le y \le 2\\2x + y \le 2\\8x + 6y \ge 9\\x + 2y \ge 2\end{array} \right.\)
Miền nghiệm là tứ giác ABCD với \(A\left( {0,6;0,7} \right)\), \(B\left( {\frac{3}{2};\frac{3}{2}} \right)\), \(C\left( {0;2} \right)\), \(D\left( {0;1,5} \right)\).
Ta có:
\(F\left( {0;1,5} \right) = 150000\), \(F\left( {0;2} \right) = 200000\), \(F\left( {\frac{3}{2};\frac{3}{2}} \right) = 200000\), \(F\left( {0,6;0,7} \right) = 190000\).
Vậy chi phí mua rẻ nhất khi x = 0; y = 1,5.
Khi đó 2.0 + 2.1,5 = 3.
Từ hai vị trí $A$ và $B$ của một tòa nhà, người ta quan sát đỉnh $C$ của ngọn núi. Biết rằng độ cao $AB = 70$ m, phương nhìn $AC$ tạo với phương nằm ngang góc $30^{{^\circ}}$, phương nhìn $BC$ tạo với phương nằm ngang góc $15^{{^\circ}}30'$. Ngọn núi đó có độ cao so với mặt đất là bao nhiêu mét? (làm tròn đến hàng đơn vị).
Áp dụng định lí sin trong tam giác.
Gọi CH là chiều cao của ngọn núi.
Theo đề ta có: \( AB = 70 \) (m), \(\widehat{CAH} = 30^o\), \( \widehat{ABC} = 90^o + 15^\prime 30^{\prime\prime} = 105,5^o \).
Suy ra \(\widehat{BAC} = 90^o - 30^o = 60^o \);
\(\widehat{ACB} = 180^o - \widehat{ABC} - \widehat{BAC} = 180^o - 105,5^o - 60^o = 14,5^o \).
Theo định lý sin trong tam giác ABC, ta có:
\(\dfrac{AB}{\sin \widehat{BCA}} = \dfrac{AC}{\sin \widehat{ABC}} \Leftrightarrow AC = \dfrac{AB \sin \widehat{ABC}}{\sin \widehat{BCA}} = \dfrac{70 \sin 105,5^o}{\sin 14,5^o} \approx 269,41\) (m).
\(\Delta A H C\) vuông tại H nên ta có:
\(CH = AC . \sin \widehat{CAH} = 269,41 . \sin 30^o \approx 135\) (m).
Vậy ngọn núi đó có độ cao so với mặt đất xấp xỉ bằng 135 m.
Cho số thực $m < 0$ và hai tập hợp $A = ( - \infty;4m),B = \left( {\dfrac{25}{m}; + \infty} \right)$. Số các giá trị nguyên của tham số $m$ để $A \cap B \neq \varnothing$?
Giao của hai tập hợp A, B là tập hợp gồm các phần tử thuộc cả A và B.
Tìm m để \(A \cap B = \emptyset\), sau đó suy ra \(A \cap B \ne \emptyset\).
\(A \cap B = \emptyset \Leftrightarrow 4m \le \frac{{25}}{m} \Leftrightarrow \frac{{4{m^2} - 25}}{m} \le 0 \Leftrightarrow 4{m^2} - 25 \ge 0\) (vì m < 0)
\( \Leftrightarrow 4{m^2} - 25 \ge 0 \Leftrightarrow \left[ \begin{array}{l}m \ge 2,5\\m \le 2,5\end{array} \right.\).
Suy ra \(A \cap B \ne \emptyset \Leftrightarrow - 2,5 \le m \le 2,5\), mà m nguyên nên có 5 giá trị m thỏa mãn.
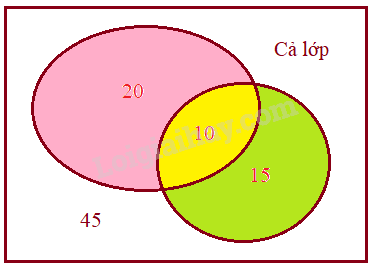
Sử dụng biểu đồ Venn để giải, hoặc áp dụng công thức:
\(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)\).
a) Số bạn đạt học lực giỏi nhưng không có hạnh kiểm tốt là:
15 - 10 = 5 (bạn).
Số bạn đạt hành kiểm tốt nhưng không có học lực giỏi là:
20 - 10 = 10 (bạn).
Số bạn được khen thưởng (chỉ đạt học lực giỏi hoặc chỉ đạt hạnh kiểm tốt hoặc đạt cả hai) là:
5 + 10 + 10 = 25 (bạn).
Cách khác:
Sử dụng công thức tính số phần tử: \(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)\).
Cụ thể:
Gọi \(A\) là tập hợp học sinh giỏi, \(B\) là tập hợp học sinh được hạnh kiểm tốt của lớp \(10A\), thì \(A ∩ B\) là tập hợp các học sinh vừa giỏi, vừa có hạnh kiểm tốt.
Số học sinh lớp \(10A\) được khen thưởng (hoặc học lực giỏi hoặc hạnh kiểm tốt) là:
\(15 + 20 - 10 = 25\) người.
b) Số bạn lớp \(10A\) chưa học giỏi và chưa có hạnh kiểm tốt là số học sinh lớp \(10A\) chưa được khen thưởng là:
\(45 - 25 = 20\) (bạn).
Biểu diễn từng miền nghiệm của mỗi bất phương trình trên cùng một mặt phẳng Oxy.
Vẽ đường thẳng \(d:x - 2y = 0\) đi qua hai điểm \(O(0;0)\) và \(B\left( {2;1} \right)\).
Xét điểm \(A(1;0).\) Ta thấy \(A \notin \Delta \) và \(1 - 2.0 = 1> 0\).
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(d\), chứa điểm A.
(miền không gạch chéo trên hình)
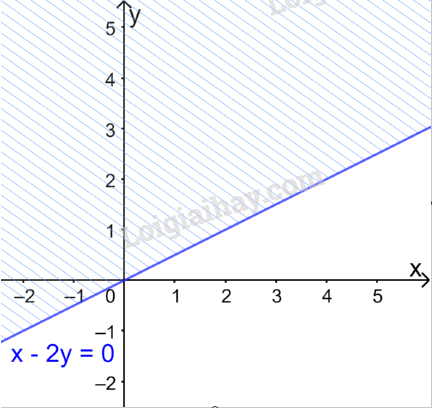
Vẽ đường thẳng \(d':x + 3y = 3\) đi qua hai điểm \(A'(0;1)\) và \(B'\left( {3;0} \right)\).
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 + 3.0 = 0 < 3\).
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(d'\), chứa gốc tọa độ O.
(miền không gạch chéo trên hình)
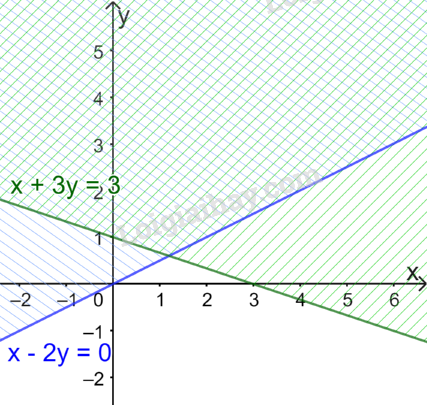
Vậy miền không gạch chéo trong hình trên là miền nghiệm của hệ bất phương trình đã cho.
Áp dụng công thức:
\({\sin ^2}x + {\cos ^2}x = 1\), \({\tan ^2}x = \frac{{{{\sin }^2}x}}{{{{\cos }^2}x}}\).
Ta có:
\(\sin x = \sqrt {1 - {{\cos }^2}x} \Rightarrow {\sin ^2}x = 1 - {\cos ^2}x\)
\(\Rightarrow {\sin ^2}x = 1 - {\left( { - \frac{1}{2}} \right)^2} = \frac{3}{4}\).
\({\tan ^2}x = \frac{{{{\sin }^2}x}}{{{{\cos }^2}x}} = \frac{{\frac{3}{4}}}{{{{\left( { - \frac{1}{2}} \right)}^2}}} = 3\).
Thay vào S:
\(S = 4{\sin ^2}x + 8{\tan ^2}x = 4.\frac{3}{4} + 8.3 = 27\).
Đề thi giữa kì 1 Toán 10 - Đề số 15
Phần trắc nghiệm
Phần trắc nghiệm
Phần trắc nghiệm
Phần trắc nghiệm (7 điểm) Câu 1: Câu nào sau đây không là mệnh đề chứa biến? A. \(x + 1 > 0\) B. x chia hết cho 2 C. \(5 - 6 > 1\) D. \(\left( {7 - x} \right)\left( {7 + x} \right) = 49 - {x^2}\)
Phần trắc nghiệm (7 điểm) Câu 1: Chọn câu trả lời đúng: A. Câu “3n chia hết cho 9” là một mệnh đề B. Câu “3n chia hết cho 9” là một mệnh đề chứa biến C. Cả A, B đều sai D. Cả A và B đều đúng
Phần trắc nghiệm (7 điểm) Câu 1: Cho mệnh đề “P(x), \(x \in X\)”. Phủ định của mệnh đề “\(\exists x \in X,P\left( x \right)\)” là: A. \(\exists x \in X,\overline {P\left( x \right)} \) B. \(\forall x \in X,\overline {P\left( x \right)} \) C. \(\forall x \in X,P\left( x \right)\) D. Cả A và C đều đúng
Phần trắc nghiệm (7 điểm) Câu 1: Cho mệnh đề “P(x), \(x \in X\)”. Chọn câu trả lời đúng. A. Phủ định của mệnh đề “\(\forall x \in X,P\left( x \right)\)” là “\(\exists x \in X,\overline {P\left( x \right)} \)”
Phần trắc nghiệm (7 điểm) Câu 1: Chọn câu trả lời đúng. A. Mệnh đề là một câu hỏi B. Mệnh đề là một câu cảm thán C. Mệnh đề là một khẳng định đúng hoặc sai D. Cả A, B, C đều đúng
Phần trắc nghiệm (7 điểm) Câu 1: Chọn câu trả lời đúng. A. Mệnh đề là một câu hỏi B. Mệnh đề là một câu cảm thán C. Mệnh đề là một khẳng định đúng hoặc sai D. Cả A, B, C đều đúng
Câu 1. Cho mệnh đề chứa biến chia hết cho 5”. Mệnh đề nào sau đây sai? A. (P(2)) B. (P(4)). C. (P(3)). D. (P(7))
Câu 1. Kí hiệu nào sau đây viết đúng mệnh đề: “\(\sqrt 2 \) là số hữu tỉ” A. \(\sqrt 2 = \mathbb{Q}\) B. \(\sqrt 2 \in \mathbb{Q}\) C. \(\sqrt 2 \subset \mathbb{Q}\) D. \(\sqrt 2 \notin \mathbb{Q}\)
Câu 1. Kí hiệu nào sau đây viết đúng mệnh đề: “(sqrt 5 ) không là số nguyên” A. (sqrt 5 = mathbb{Z}) B. (sqrt 5 in mathbb{Z}) C. (sqrt 5 subset mathbb{Z}) D. (sqrt 5 notin mathbb{Z})
Câu 1. Kí hiệu nào sau đây viết đúng mệnh đề: “(sqrt 2 ) không là số hữu tỉ” A. (sqrt 2 = mathbb{Q}) B. (sqrt 2 in mathbb{Q}) C. (sqrt 2 subset mathbb{Q}) D. (sqrt 2 notin mathbb{Q})
Câu 1. Mệnh đề nào sau đây là phủ định của mệnh đề: “(exists x in mathbb{R}|{x^2} - 3x + 2 > 0)” A. (exists x in mathbb{R}|{x^2} - 3x + 2 < 0) B. (exists x in mathbb{R}|{x^2} - 3x + 2 le 0) C. (forall x in mathbb{R}|{x^2} - 3x + 2 le 0) D. (forall x in mathbb{R}|{x^2} - 3x + 2 > 0)
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
