-
Đề khảo sát chất lượng đầu năm
-
Đề thi giữa kì 1
- Đề thi giữa kì 1 - Đề số 1
- Đề thi giữa kì 1 - Đề số 2
- Đề thi giữa kì 1 - Đề số 3
- Đề thi giữa kì 1 - Đề số 4
- Đề thi giữa kì 1 - Đề số 5
- Đề thi giữa kì 1 - Đề số 6
- Đề thi giữa kì 1 - Đề số 6
- Đề thi giữa kì 1 - Đề số 7
- Đề thi giữa kì 1 - Đề số 8
- Đề thi giữa kì 1 - Đề số 9
- Đề thi giữa kì 1 - Đề số 10
- Đề thi giữa kì 1 - Đề số 11
- Đề thi giữa kì 1 - Đề số 12
- Đề thi giữa kì 1 - Đề số 13
- Đề thi giữa kì 1 - Đề số 14
- Đề thi giữa kì 1 - Đề số 15
-
Đề thi học kì 1
- Đề cương ôn tập học kì 1
- Đề thi học kì 1 Toán 10 - Đề số 1
- Đề thi học kì 1 Toán 10 - Đề số 2
- Đề thi học kì 1 Toán 10 - Đề số 3
- Đề thi học kì 1 Toán 10 - Đề số 4
- Đề thi học kì 1 Toán 10 - Đề số 5
- Đề thi học kì 1 Toán 10 - Đề số 6
- Đề thi học kì 1 Toán 10 - Đề số 7
- Đề thi học kì 1 Toán 10 - Đề số 8
- Đề thi học kì 1 Toán 10 - Đề số 9
- Đề thi học kì 1 Toán 10 - Đề số 10
- Đề thi học kì 1 Toán 10 - Đề số 11
- Đề thi học kì 1 Toán 10 - Đề số 12
- Đề thi học kì 1 Toán 10 - Đề số 13
-
Đề thi giữa kì 2
-
Đề thi học kì 2
Đề thi giữa kì 1 Toán 10 - Đề số 15
Tổng hợp đề thi giữa kì 1 lớp 10 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Đề thi giữa kì 1 Toán 10 - Đề số 15
Đề bài
Kí hiệu nào sau đây là để chỉ \(\sqrt 5 \) không phải là số hữu tỉ?
-
A.
\(\sqrt 5 \ne Q\).
-
B.
\(\sqrt 5 \not\subset Q\).
-
C.
\(\sqrt 5 \notin Q\).
-
D.
Kí hiệu khác.
Trong tam giác ABC với BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp tam giác ABC. Hệ thức nào sau đây đúng?
-
A.
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = R\)
-
B.
\(\frac{a}{{\cos A}} = \frac{b}{{\cos B}} = \frac{c}{{\cos C}} = R\)
-
C.
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
-
D.
\(\frac{a}{{\cos A}} = \frac{b}{{\cos B}} = \frac{c}{{\cos C}} = 2R\)
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
-
A.
\(x - {y^2} < 0\)
-
B.
\(x + y < 3xy\)
-
C.
\(x + \frac{1}{y} \ge 0\)
-
D.
\(\frac{x}{3} + \frac{y}{2} < 0\)
Cho tam giác ABC có AB = c, AC = b, CB = a. Chọn mệnh đề sai?
-
A.
\({a^2} = {b^2} + {c^2} - 2bc\cos A\)
-
B.
\({b^2} = {a^2} + {c^2} - 2ac\cos B\)
-
C.
\({c^2} = {a^2} + {b^2} - 2ab\cos B\)
-
D.
\({c^2} = {b^2} + {a^2} - 2ba\cos C\)
Trong các đẳng thức sau, đẳng thức nào đúng?
-
A.
\(\sin ({180^o} - \alpha ) = - \sin \alpha \)
-
B.
\(\cos ({180^o} - \alpha ) = \cos \alpha \)
-
C.
\(\sin ({90^o} - \alpha ) = \cos \alpha \)
-
D.
\(\sin ({90^o} - \alpha ) = \sin \alpha \)
Cặp số nào sau đây là một nghiệm của bất phương trình \(x + 2y \le 4\)?
-
A.
\((2;1)\)
-
B.
\((1;2)\)
-
C.
\((1;3)\)
-
D.
\(( - 1;3)\)
Viết mệnh đề sau bằng kí hiệu \(\forall \) hoặc \(\exists \): “Có một số nguyên bằng bình phương của chính nó”.
-
A.
\(\exists x \in \mathbb{R},{x^2} - x = 0\)
-
B.
\(\exists x \in \mathbb{R},x = {x^2}\)
-
C.
\(\forall x \in \mathbb{Z},{x^2} = x\)
-
D.
\(\exists x \in \mathbb{Z},x = {x^2}\)
Miền nghiệm của bất phương trình $3x + 2y > - 6$ (miền không bị gạch bỏ) là
-
A.
-
B.
-
C.
-
D.
Phát biểu nào sau đây là một mệnh đề?
-
A.
Trời hôm nay đẹp quá!
-
B.
New York là thủ đô của Việt Nam.
-
C.
Con đang làm gì đó?
-
D.
Số 3 có phải số tự nhiên không?
Xác định tập số sau: \(\mathbb{R}\backslash \left[ {1;3} \right]\).
-
A.
\(\left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\)
-
B.
\(\left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)\)
-
C.
\(\left( {1;3} \right)\)
-
D.
\(\left[ {1;3} \right]\)
-
A.
A1 = {1; 6}
-
B.
A2 = {0; 1; 3}
-
C.
A3 = {4; 5}
-
D.
A4 = {0}
Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?
-
A.
Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau
-
B.
Nếu hai tam giác bằng nhau thì chu vi của chúng bằng nhau
-
C.
Nếu hai tam giác bằng nhau thì chúng có các góc tương ứng bằng nhau
-
D.
Nếu hai tam giác bằng nhau thì chúng có các cặp cạnh tương ứng bằng nhau.
Cho hệ bất phương trình $\left\{ \begin{array}{l} {2x + 3y - 6 \leq 0} \\ {x \geq 0} \\ {2x - 3y - 1 \leq 0} \end{array} \right.$. Các mệnh đề sau đúng hay sai?
a) Hệ trên là một hệ bất phương trình bậc nhất hai ẩn.
b) (0;0) là một nghiệm của hệ bất phương trình trên.
c) (1;-1) là một nghiệm của hệ bất phương trình trên.
d) Với x, y thỏa mãn hệ bất phương trình đã cho, biểu thức $L = y - x$ đạt giá trị lớn nhất là a và đạt giá trị nhỏ nhất là b và $a + 2b = \dfrac{13}{12}$.
Cho tam giác $ABC$ có b = 7 cm, c = 5cm, $\widehat{A} = 120^{o}$. Khi đó:
a) $a = \sqrt{127}$ cm.
b) $\cos C \approx 0,91$.
c) $\cos B \approx 0,21$.
d) Bán kính đường tròn ngoại tiếp tam giác $ABC$ là $R \approx 6,03$ (cm).
Ông An vừa được cấp một mảnh đất trồng lúa có dạng hình thang ABCD với AD // BC (xem minh họa hình bên dưới). Cạnh AB dọc theo đường đi và có độ dài 70 m. Sử dụng giác kế, người ta đo được các góc $\widehat{DAC} = 22^{o}$, $\widehat{BAC} = 54^{o}$ và $\widehat{ABD} = 73^{o}$.
Hãy giúp ông An tính gần đúng diện tích mảnh đất (đơn vị mét vuông, kết quả chính xác đến hàng đơn vị).
Để gây quỹ từ thiện, câu lạc bộ thiện nguyện của một trường THPT tổ chức hoạt động bán hàng với hai mặt hàng là nước chanh và khoai chiên. Câu lạc bộ thiết kế hai thực đơn. Thực đơn 1 có giá 25 nghìn đồng, bao gồm hai cốc nước chanh và một túi khoai chiên. Thực đơn 2 có giá 40 nghìn đồng, bao gồm ba cốc nước chanh và hai túi khoai chiên. Biết rằng câu lạc bộ chỉ làm được không quá 165 cốc nước chanh và 100 túi khoai chiên. Số tiền lớn nhất mà câu lạc bộ có thể nhận được sau khi bán hết hàng bằng bao nhiêu nghìn đồng?
Tính khoảng cách từ vị trí của một người đang gọi điện thoại di động đến trạm phát sóng B với số liệu đã cho trong hình vẽ (đơn vị: km; làm tròn kết quả đến hàng phần trăm).
Cho tập hợp $A = \left\{ x \in Z \mid x^{2} + 4x - 5 = 0 \right\}$ và tập hợp $B = \left\{ {x \in Z \mid \left( {6x^{2} - 7x + 1} \right)\left( {2x + 1} \right) = 0} \right\}$. Tập hợp $A \cap B$ có bao nhiêu phần tử?
Lời giải và đáp án
Kí hiệu nào sau đây là để chỉ \(\sqrt 5 \) không phải là số hữu tỉ?
-
A.
\(\sqrt 5 \ne Q\).
-
B.
\(\sqrt 5 \not\subset Q\).
-
C.
\(\sqrt 5 \notin Q\).
-
D.
Kí hiệu khác.
Đáp án : C
Sử dụng kí hiệu phần tử không thuộc tập hợp:
+ Phần tử thuộc tập hợp thì có kí hiệu \( \in \).
+ Phần tử không thuộc tập hợp thì có kí hiệu \( \notin \).
Vì \(\sqrt 5 \) không là số hữu tỉ nên \(\sqrt 5 \notin Q\).
Trong tam giác ABC với BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp tam giác ABC. Hệ thức nào sau đây đúng?
-
A.
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = R\)
-
B.
\(\frac{a}{{\cos A}} = \frac{b}{{\cos B}} = \frac{c}{{\cos C}} = R\)
-
C.
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
-
D.
\(\frac{a}{{\cos A}} = \frac{b}{{\cos B}} = \frac{c}{{\cos C}} = 2R\)
Đáp án : C
Dựa vào định lí sin trong tam giác.
Trong tam giác ABC với BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp tam giác ABC, ta có \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\).
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
-
A.
\(x - {y^2} < 0\)
-
B.
\(x + y < 3xy\)
-
C.
\(x + \frac{1}{y} \ge 0\)
-
D.
\(\frac{x}{3} + \frac{y}{2} < 0\)
Đáp án : D
Dựa vào định nghĩa bất phương trình bậc nhất hai ẩn.
Các bất phương trình ở đáp án A, B, C không phải bất phương trình bậc nhất hai ẩn.
Cho tam giác ABC có AB = c, AC = b, CB = a. Chọn mệnh đề sai?
-
A.
\({a^2} = {b^2} + {c^2} - 2bc\cos A\)
-
B.
\({b^2} = {a^2} + {c^2} - 2ac\cos B\)
-
C.
\({c^2} = {a^2} + {b^2} - 2ab\cos B\)
-
D.
\({c^2} = {b^2} + {a^2} - 2ba\cos C\)
Đáp án : C
Sử dụng định lí cosin trong tam giác ABC.
Theo định lí cosin: \({c^2} = {a^2} + {b^2} - 2ab\cos C\) nên C sai.
Trong các đẳng thức sau, đẳng thức nào đúng?
-
A.
\(\sin ({180^o} - \alpha ) = - \sin \alpha \)
-
B.
\(\cos ({180^o} - \alpha ) = \cos \alpha \)
-
C.
\(\sin ({90^o} - \alpha ) = \cos \alpha \)
-
D.
\(\sin ({90^o} - \alpha ) = \sin \alpha \)
Đáp án : C
Dựa vào mối quan hệ giữa các giá trị lượng giác của hai góc phụ nhau, hai góc bù nhau.
Ta có:
\(\sin ({180^o} - \alpha ) = \sin \alpha \) suy ra A sai.
\(\cos ({180^o} - \alpha ) = - \cos \alpha \) suy ra B sai.
\(\sin ({90^o} - \alpha ) = \cos \alpha \) suy ra C đúng, D sai.
Cặp số nào sau đây là một nghiệm của bất phương trình \(x + 2y \le 4\)?
-
A.
\((2;1)\)
-
B.
\((1;2)\)
-
C.
\((1;3)\)
-
D.
\(( - 1;3)\)
Đáp án : A
Thay từng cặp số vào bất phương trình xem cặp số nào thỏa mãn.
Xét \((2;1)\) ta có \(2 + 2.1 \le 4\) (đúng).
Xét \((1;2)\) ta có \(1 + 2.2 \le 4\) (sai).
Xét \((1;3)\) ta có \(1 + 2.3 \le 4\) (sai).
Xét \(( - 1;3)\) ta có \( - 1 + 2.3 \le 4\) (sai).
Vậy cặp số (2;1) là một nghiệm của bất phương trình \(x + 2y \le 4\).
Viết mệnh đề sau bằng kí hiệu \(\forall \) hoặc \(\exists \): “Có một số nguyên bằng bình phương của chính nó”.
-
A.
\(\exists x \in \mathbb{R},{x^2} - x = 0\)
-
B.
\(\exists x \in \mathbb{R},x = {x^2}\)
-
C.
\(\forall x \in \mathbb{Z},{x^2} = x\)
-
D.
\(\exists x \in \mathbb{Z},x = {x^2}\)
Đáp án : D
Đọc kĩ mệnh đề và áp dụng quy tắc sử dụng kí hiệu \(\forall \) và \(\exists \).
“Có một số nguyên” tức là tồn tại số nguyên: \(\exists x \in \mathbb{Z}\).
“Số (nguyên) bằng bình phương của chính nó”: \(x = {x^2}\).
Vậy mệnh đề đúng là “\(\exists x \in \mathbb{Z},x = {x^2}\)”.
Miền nghiệm của bất phương trình $3x + 2y > - 6$ (miền không bị gạch bỏ) là
-
A.
-
B.
-
C.
-
D.
Đáp án : A
Xác định miền nghiệm.
Đường thẳng \(3x + 2y + 6 = 0\) đi qua hai điểm (0;-3) và (-2;0) nên ta chọn đáp án A.
Phát biểu nào sau đây là một mệnh đề?
-
A.
Trời hôm nay đẹp quá!
-
B.
New York là thủ đô của Việt Nam.
-
C.
Con đang làm gì đó?
-
D.
Số 3 có phải số tự nhiên không?
Đáp án : B
Mệnh đề là một khẳng định có tính đúng sai.
B là một mệnh đề. Các đáp án còn lại là câu cảm thán hoặc câu hỏi.
Xác định tập số sau: \(\mathbb{R}\backslash \left[ {1;3} \right]\).
-
A.
\(\left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\)
-
B.
\(\left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)\)
-
C.
\(\left( {1;3} \right)\)
-
D.
\(\left[ {1;3} \right]\)
Đáp án : A
\(A\backslash B = \left\{ {x \in R\backslash x \in A;\,x \notin B} \right\}.\)
Ta có: \(\mathbb{R}\backslash \left[ {1;3} \right] = \left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right).\)
Biểu diễn trên trục số:
-
A.
A1 = {1; 6}
-
B.
A2 = {0; 1; 3}
-
C.
A3 = {4; 5}
-
D.
A4 = {0}
Đáp án : C
Tập con của A là tập gồm các phần tử đều thuộc A.
Vì \(6 \notin A\) nên \({A_1}\not{ \subset }A\).
Vì \(0 \notin A\) nên \({A_2}\not{ \subset }A\), \({A_4}\not{ \subset }A\).
Vì \(4 \in A\), \(5 \in A\) nên \({A_3} \subset A\).
Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?
-
A.
Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau
-
B.
Nếu hai tam giác bằng nhau thì chu vi của chúng bằng nhau
-
C.
Nếu hai tam giác bằng nhau thì chúng có các góc tương ứng bằng nhau
-
D.
Nếu hai tam giác bằng nhau thì chúng có các cặp cạnh tương ứng bằng nhau.
Đáp án : D
Mệnh đề đảo của mệnh đề “Nếu P thì Q” là mệnh đề “Nếu Q thì P”.
A. Mệnh đề đảo là: “Nếu hai tam giác có diện tích bằng nhau thì chúng bằng nhau”.
Mệnh đề này sai, chẳng hạn:
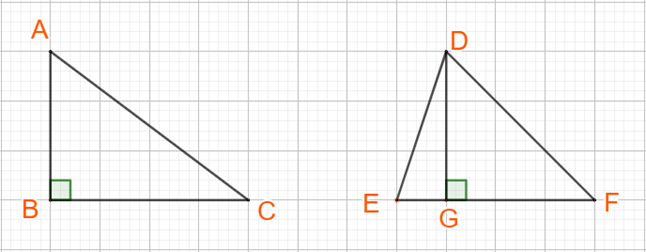
B. Mệnh đề đảo là: “Nếu hai tam giác có chu vi bằng nhau thì chúng bằng nhau”.
Mệnh đề này sai, chẳng hạn:
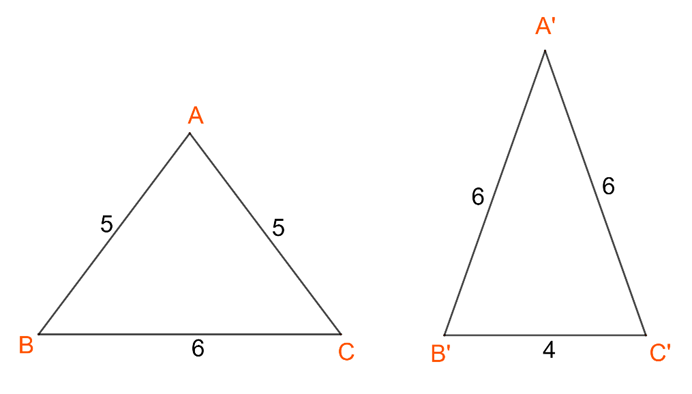
C. Mệnh đề đảo là: “Nếu hai tam giác có các góc tương ứng bằng nhau thì chúng bằng nhau”.
Mệnh đề này sai, chẳng hạn:
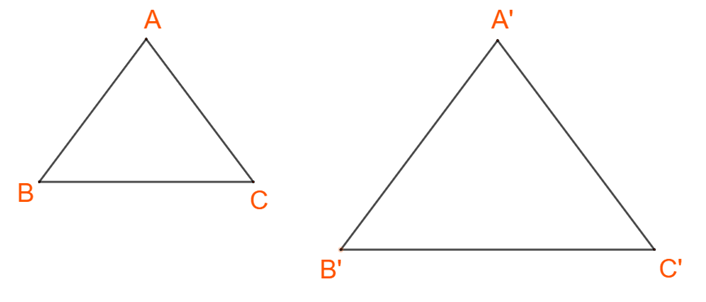
D. Mệnh đề đảo là: “Nếu hai tam giác có các cặp cạnh tương ứng bằng nhau thì chúng bằng nhau”.
Mệnh đề này đúng.
Cho hệ bất phương trình $\left\{ \begin{array}{l} {2x + 3y - 6 \leq 0} \\ {x \geq 0} \\ {2x - 3y - 1 \leq 0} \end{array} \right.$. Các mệnh đề sau đúng hay sai?
a) Hệ trên là một hệ bất phương trình bậc nhất hai ẩn.
b) (0;0) là một nghiệm của hệ bất phương trình trên.
c) (1;-1) là một nghiệm của hệ bất phương trình trên.
d) Với x, y thỏa mãn hệ bất phương trình đã cho, biểu thức $L = y - x$ đạt giá trị lớn nhất là a và đạt giá trị nhỏ nhất là b và $a + 2b = \dfrac{13}{12}$.
a) Hệ trên là một hệ bất phương trình bậc nhất hai ẩn.
b) (0;0) là một nghiệm của hệ bất phương trình trên.
c) (1;-1) là một nghiệm của hệ bất phương trình trên.
d) Với x, y thỏa mãn hệ bất phương trình đã cho, biểu thức $L = y - x$ đạt giá trị lớn nhất là a và đạt giá trị nhỏ nhất là b và $a + 2b = \dfrac{13}{12}$.
Thay các cặp số vào hệ phương trình, nếu thỏa mãn thì là nghiệm của hệ.
Giá trị nhỏ nhất hay lớn nhất của biểu thức P(x;y) = ax + by (b ≠ 0) trên miền nghiệm đa giác (kể cả biên) đạt được tại một đỉnh nào đó của đa giác.
a) Đúng. Hệ trên là hệ bất phương trình bậc nhất hai ẩn.
b) Đúng. Thay \((0;0)\) vào hệ trên ta được \(\left\{ \begin{array}{l} - 6 \le 0\\0 \ge 0\\ - 1 \le 0\end{array} \right.\) (đúng).
c) Sai. Thay \((1; - 1)\) vào hệ trên ta được \(\left\{ \begin{array}{l}2.1 + 3.( - 1) - 6 \le 0\\1 \ge 0\\2.1 - 3.( - 1) - 1 \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 7 \le 0\\1 \ge 0\\4 \le 0\end{array} \right.\) (sai).
d) Đúng. Miền nghiệm của hệ bất phương trình được biểu diễn như hình sau:
Trước hết, ta vẽ ba đường thẳng: \(\left( {{d_1}} \right):2x + 3y - 6 = 0\); \(\left( {{d_2}} \right):x = 0\); \(\left( {{d_3}} \right):2x - 3y - 1 = 0\).
Ta thấy \(\left( {0;0} \right)\) là nghiệm của cả ba bất phương trình. Điều đó có nghĩa gốc tọa độ thuộc cả ba miền nghiệm của cả ba bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ.
Miền nghiệm là hình tam giác \(ABC\), với \(A\left( {0;2} \right)\), \(B\left( {\frac{7}{4};\frac{5}{6}} \right)\), \(C\left( {0; - \frac{1}{3}} \right)\).
Vậy ta có \(a = 2 - 0 = 2\), \(b = \frac{5}{6} - \frac{7}{4} = - \frac{{11}}{{12}} \Rightarrow a + b = \frac{{13}}{{12}}\).
Cho tam giác $ABC$ có b = 7 cm, c = 5cm, $\widehat{A} = 120^{o}$. Khi đó:
a) $a = \sqrt{127}$ cm.
b) $\cos C \approx 0,91$.
c) $\cos B \approx 0,21$.
d) Bán kính đường tròn ngoại tiếp tam giác $ABC$ là $R \approx 6,03$ (cm).
a) $a = \sqrt{127}$ cm.
b) $\cos C \approx 0,91$.
c) $\cos B \approx 0,21$.
d) Bán kính đường tròn ngoại tiếp tam giác $ABC$ là $R \approx 6,03$ (cm).
Áp dụng định lí và hệ quả định lí cosin, định lí sin.
a) Sai. \(a = \sqrt {{b^2} + {c^2} - 2bc\cos A} = \sqrt {{7^2} + {5^2} - 2.7.5\cos {{120}^o}} = \sqrt {109} \) (cm).
b) Đúng. \(\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} = \frac{{109 + {7^2} - {5^2}}}{{2\sqrt {109} .7}} \approx 0,91\).
c) Sai. \(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} = \frac{{109 + {5^2} - {7^2}}}{{2\sqrt {109} .5}} \approx 0,81\).
d) Đúng. \(\frac{a}{{\sin A}} = 2R \Leftrightarrow R = \frac{a}{{2\sin A}} = \frac{{\sqrt {109} }}{{2.\sin {{120}^o}}} = \frac{{\sqrt {327} }}{3} \approx 6,03\) (cm).
Ông An vừa được cấp một mảnh đất trồng lúa có dạng hình thang ABCD với AD // BC (xem minh họa hình bên dưới). Cạnh AB dọc theo đường đi và có độ dài 70 m. Sử dụng giác kế, người ta đo được các góc $\widehat{DAC} = 22^{o}$, $\widehat{BAC} = 54^{o}$ và $\widehat{ABD} = 73^{o}$.
Hãy giúp ông An tính gần đúng diện tích mảnh đất (đơn vị mét vuông, kết quả chính xác đến hàng đơn vị).
Áp dụng định lí sin và công thức tính diện tích tam giác.
Ta có \(\widehat {BAD} = 54^\circ + 22^\circ = 76^\circ \Rightarrow \widehat {ABC} = 180^\circ - 76^\circ = 104^\circ \), \(\widehat {ACB} = \widehat {DAC} = 22^\circ \).
Áp dụng định lý sin cho tam giác ABC, ta có \(\frac{{AC}}{{\sin 104^\circ }} = \frac{{AB}}{{\sin 22^\circ }} \Rightarrow AC = \frac{{70.\sin 104^\circ }}{{\sin 22^\circ }}\).
Suy ra diện tích tam giác ABC là \({S_{ABC}} = \frac{1}{2}AB.AC.\sin 54^\circ = \frac{{70.\sin 104^\circ .\sin 54^\circ }}{{2.\sin 22^\circ }}\).
Lại có \(\widehat {ADB} = 180^\circ - 76^\circ - 73^\circ = 31^\circ \).
Áp dụng định lý sin cho tam giác ABD, ta có:
\(\frac{{AD}}{{\sin 73^\circ }} = \frac{{AB}}{{\sin 31^\circ }} \Rightarrow AD = \frac{{70.\sin 73^\circ }}{{\sin 31^\circ }} \approx 129,97(m).\)
Suy ra diện tích tam giác ACD là \({S_{ACD}} = \frac{1}{2}AC.AD.\sin 22^\circ = \frac{{{{70}^2}.\sin 104^\circ .\sin 73^\circ }}{{2.\sin 22^\circ .\sin 31^\circ }}\).
Vậy diện tích mảnh đất là \({S_{ABCD}} = {S_{ABC}} + {S_{ACD}} \approx 9548\,\,({m^2})\).
Để gây quỹ từ thiện, câu lạc bộ thiện nguyện của một trường THPT tổ chức hoạt động bán hàng với hai mặt hàng là nước chanh và khoai chiên. Câu lạc bộ thiết kế hai thực đơn. Thực đơn 1 có giá 25 nghìn đồng, bao gồm hai cốc nước chanh và một túi khoai chiên. Thực đơn 2 có giá 40 nghìn đồng, bao gồm ba cốc nước chanh và hai túi khoai chiên. Biết rằng câu lạc bộ chỉ làm được không quá 165 cốc nước chanh và 100 túi khoai chiên. Số tiền lớn nhất mà câu lạc bộ có thể nhận được sau khi bán hết hàng bằng bao nhiêu nghìn đồng?
Ứng dụng hệ bất phương trình bậc nhất hai ẩn.
Gọi số thực đơn 1 là $x$, số thực đơn 2 là $y$, ta có $x \geq 0$; $y \geq 0$.
Số cốc nước chanh là $2x + 3y \leq 165$.
Số túi khoai tây chiên là $x + 2y \leq 100$.
Số tiền thu về là $T = 25x + 40y$.
Xét hệ bất phương trình bậc nhất một ẩn:
$\left\{ \begin{array}{l} {x \geq 0} \\ {y \geq 0} \\ {2x + 3y \leq 165} \\ {x + 2y \leq 100} \end{array} \right.$
Miền nghiệm là tứ giác OABC với O(0;0), A(0;50), B(30;35), C(82,5;0).
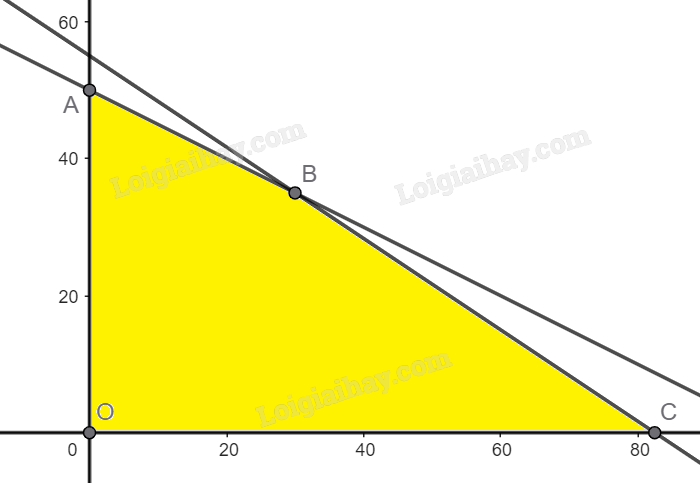
Ta có: $T_{O} = 25.0 + 40.0 = 0$;
$T_{A} = 25.0 + 40.50 = 200$;
$T_{B} = 25.30 + 40.35 = 2150$;
$T_{C} = 25.82,5 + 40.0 = 2062,5$.
Vậy số tiền lớn nhất câu lạc bộ nhận được khi bán hết hàng bằng 2150 nghìn đồng.
Tính khoảng cách từ vị trí của một người đang gọi điện thoại di động đến trạm phát sóng B với số liệu đã cho trong hình vẽ (đơn vị: km; làm tròn kết quả đến hàng phần trăm).
Áp dụng định lí cosin.
Áp dụng định lí cosin trong tam giác MAB, ta có:
\(MB = \sqrt {A{B^2} + A{M^2} - 2.AB.AM.\cos A} \)
\(= \sqrt {{2^2} + 1,{8^2} - 2.2.1,8.\cos {{32}^o}} \approx 1,06\) (km).
Vậy khoảng cách từ vị trí của người đó đến trạm phát sóng B là 1,06 km.
Cho tập hợp $A = \left\{ x \in Z \mid x^{2} + 4x - 5 = 0 \right\}$ và tập hợp $B = \left\{ {x \in Z \mid \left( {6x^{2} - 7x + 1} \right)\left( {2x + 1} \right) = 0} \right\}$. Tập hợp $A \cap B$ có bao nhiêu phần tử?
Viết tập hợp A, B bằng cách liệt kê phần tử, từ đó tìm $A \cap B$ là tập hợp bao gồm các phần tử thuộc cả A và B.
\(A = \{ - 5;1\} \), \(B = \left\{ { - \frac{1}{2};\frac{1}{6};1} \right\}\).
\(A \cap B = 1\).
Áp dụng các công thức sau:
\(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right) \).
\(n\left( {A\backslash B} \right) = n\left( A \right) - n\left( {A \cap B} \right)\).
Gọi A là tập hợp các học sinh thích bóng rổ, suy ra \(n\left( A \right) = 20\).
B là tập hợp các học sinh thích bóng bàn, suy ra \(n\left( B \right) = 14\).
C là tập hợp các học sinh không thích môn nào trong hai môn thể thao trên, suy ra \(n\left( C \right) = 10\).
D là tập hợp tất cả học sinh của lớp, suy ra \(n\left( D \right) = 36\).
a) Số học sinh thích một trong hai môn trên là:
\(n\left( {A \cup B} \right) = n\left( D \right) - n\left( C \right) = 36 - 10 = 26\).
Số học sinh thích cả hai môn là:
\(n\left( {A \cap B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cup B} \right) = 20 + 14 - 26 = 8\).
b) Số học sinh thích bóng rổ nhưng không thích bóng bàn là:
\(n\left( {A\backslash B} \right) = n\left( A \right) - n\left( {A \cap B} \right) = 20 - 8 = 12\).
Bước 1: Vẽ các đường thẳng.
Bước 2: Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.
Bước 3: Phần không bị gạch là miền nghiệm.
Vẽ đường thẳng \(3x - y = - 3\) (nét đứt).
Thay tọa độ điểm O(0;0) vào \(3x - y > - 3\) ta được \(3.0 - 0 > - 3\) (Đúng).
Gạch đi phần không chứa O.
Vẽ đường thẳng \( - 2x + 3y = 6\) (nét đứt).
Thay tọa độ điểm O(0;0) vào \( - 2x + 3y < 6\) ta được \( - 2.0 + 3.0 < 6\) (Đúng).
Gạch đi phần không chứa O.
Vẽ đường thẳng \(2x + y = - 4\) (nét đứt).
Thay tọa độ điểm O(0;0) vào \(2x + y > - 4\) ta được \(2.0 + 0 > - 4\) (Đúng).
Gạch đi phần không chứa O.
Miền nghiệm của hệ là phần không bị gạch chéo:
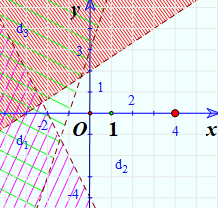
Bước 1: Chia cả tử và mẫu của biểu thức P cho \(\cos \alpha \).
Bước 2: Biến đổi biểu thức P sao cho xuất hiện duy nhất giá trị \(\tan \alpha \).
Bước 3: Thay \(\tan \alpha = - 2\) rồi tính giá trị biểu thức P.
Do \(\tan \alpha = - 2\) nên \(\cos \alpha \ne 0\). Chia cả tử và mẫu của biểu thức P cho \(\cos \alpha \) ta có:
\(P = \frac{{\frac{{\cos \alpha + 3\sin \alpha }}{{\cos \alpha }}}}{{\frac{{\sin \alpha + 3\cos \alpha }}{{\cos \alpha }}}} = \frac{{1 + 3\frac{{\sin \alpha }}{{\cos \alpha }}}}{{\frac{{\sin \alpha }}{{\cos \alpha }} + 3}} \)
\(= \frac{{1 + 3\tan \alpha }}{{\tan \alpha + 3}} = \frac{{1 + 3.( - 2)}}{{ - 2 + 3}} = - 5\)
Vậy với \(\tan \alpha = - 2\) thì P = -5.
Đề thi giữa kì 1 Toán 10 - Đề số 14
Phần trắc nghiệm
Phần trắc nghiệm
Phần trắc nghiệm
Phần trắc nghiệm (7 điểm) Câu 1: Câu nào sau đây không là mệnh đề chứa biến? A. \(x + 1 > 0\) B. x chia hết cho 2 C. \(5 - 6 > 1\) D. \(\left( {7 - x} \right)\left( {7 + x} \right) = 49 - {x^2}\)
Phần trắc nghiệm (7 điểm) Câu 1: Chọn câu trả lời đúng: A. Câu “3n chia hết cho 9” là một mệnh đề B. Câu “3n chia hết cho 9” là một mệnh đề chứa biến C. Cả A, B đều sai D. Cả A và B đều đúng
Phần trắc nghiệm (7 điểm) Câu 1: Cho mệnh đề “P(x), \(x \in X\)”. Phủ định của mệnh đề “\(\exists x \in X,P\left( x \right)\)” là: A. \(\exists x \in X,\overline {P\left( x \right)} \) B. \(\forall x \in X,\overline {P\left( x \right)} \) C. \(\forall x \in X,P\left( x \right)\) D. Cả A và C đều đúng
Phần trắc nghiệm (7 điểm) Câu 1: Cho mệnh đề “P(x), \(x \in X\)”. Chọn câu trả lời đúng. A. Phủ định của mệnh đề “\(\forall x \in X,P\left( x \right)\)” là “\(\exists x \in X,\overline {P\left( x \right)} \)”
Phần trắc nghiệm (7 điểm) Câu 1: Chọn câu trả lời đúng. A. Mệnh đề là một câu hỏi B. Mệnh đề là một câu cảm thán C. Mệnh đề là một khẳng định đúng hoặc sai D. Cả A, B, C đều đúng
Phần trắc nghiệm (7 điểm) Câu 1: Chọn câu trả lời đúng. A. Mệnh đề là một câu hỏi B. Mệnh đề là một câu cảm thán C. Mệnh đề là một khẳng định đúng hoặc sai D. Cả A, B, C đều đúng
Câu 1. Cho mệnh đề chứa biến chia hết cho 5”. Mệnh đề nào sau đây sai? A. (P(2)) B. (P(4)). C. (P(3)). D. (P(7))
Câu 1. Kí hiệu nào sau đây viết đúng mệnh đề: “\(\sqrt 2 \) là số hữu tỉ” A. \(\sqrt 2 = \mathbb{Q}\) B. \(\sqrt 2 \in \mathbb{Q}\) C. \(\sqrt 2 \subset \mathbb{Q}\) D. \(\sqrt 2 \notin \mathbb{Q}\)
Câu 1. Kí hiệu nào sau đây viết đúng mệnh đề: “(sqrt 5 ) không là số nguyên” A. (sqrt 5 = mathbb{Z}) B. (sqrt 5 in mathbb{Z}) C. (sqrt 5 subset mathbb{Z}) D. (sqrt 5 notin mathbb{Z})
Câu 1. Kí hiệu nào sau đây viết đúng mệnh đề: “(sqrt 2 ) không là số hữu tỉ” A. (sqrt 2 = mathbb{Q}) B. (sqrt 2 in mathbb{Q}) C. (sqrt 2 subset mathbb{Q}) D. (sqrt 2 notin mathbb{Q})
Câu 1. Mệnh đề nào sau đây là phủ định của mệnh đề: “(exists x in mathbb{R}|{x^2} - 3x + 2 > 0)” A. (exists x in mathbb{R}|{x^2} - 3x + 2 < 0) B. (exists x in mathbb{R}|{x^2} - 3x + 2 le 0) C. (forall x in mathbb{R}|{x^2} - 3x + 2 le 0) D. (forall x in mathbb{R}|{x^2} - 3x + 2 > 0)
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
