-
Đề khảo sát chất lượng đầu năm
-
Đề thi giữa kì 1
- Đề thi giữa kì 1 - Đề số 1
- Đề thi giữa kì 1 - Đề số 2
- Đề thi giữa kì 1 - Đề số 3
- Đề thi giữa kì 1 - Đề số 4
- Đề thi giữa kì 1 - Đề số 5
- Đề thi giữa kì 1 - Đề số 6
- Đề thi giữa kì 1 - Đề số 6
- Đề thi giữa kì 1 - Đề số 7
- Đề thi giữa kì 1 - Đề số 8
- Đề thi giữa kì 1 - Đề số 9
- Đề thi giữa kì 1 - Đề số 10
- Đề thi giữa kì 1 - Đề số 11
- Đề thi giữa kì 1 - Đề số 12
- Đề thi giữa kì 1 - Đề số 13
- Đề thi giữa kì 1 - Đề số 14
- Đề thi giữa kì 1 - Đề số 15
-
Đề thi học kì 1
- Đề cương ôn tập học kì 1
- Đề thi học kì 1 Toán 10 - Đề số 1
- Đề thi học kì 1 Toán 10 - Đề số 2
- Đề thi học kì 1 Toán 10 - Đề số 3
- Đề thi học kì 1 Toán 10 - Đề số 4
- Đề thi học kì 1 Toán 10 - Đề số 5
- Đề thi học kì 1 Toán 10 - Đề số 6
- Đề thi học kì 1 Toán 10 - Đề số 7
- Đề thi học kì 1 Toán 10 - Đề số 8
- Đề thi học kì 1 Toán 10 - Đề số 9
- Đề thi học kì 1 Toán 10 - Đề số 10
- Đề thi học kì 1 Toán 10 - Đề số 11
- Đề thi học kì 1 Toán 10 - Đề số 12
- Đề thi học kì 1 Toán 10 - Đề số 13
- Đề thi học kì 1 Toán 10 - Đề số 14
- Đề thi học kì 1 Toán 10 - Đề số 15
-
Đề thi giữa kì 2
-
Đề thi học kì 2
Đề thi học kì 1 Toán 10 Kết nối tri thức - Đề số 15
Đề thi học kì 1 Toán 10 Kết nối tri thức - Đề số 15
Đề bài
Mệnh đề phủ định của P: "$\forall x \in \mathbb{R}, x^2 > 0$" là
-
A.
$\overline{P} $: "$\exists x \in \mathbb{R}, x^2 \leq 0$".
-
B.
$\overline{P} $: "$\exists x \in \mathbb{R}, x^2 < 0$".
-
C.
$\overline{P} $: "$\forall x \in \mathbb{R}, x^2 \leq 0$".
-
D.
$\overline{P} $: "$\forall x \in \mathbb{R}, x^2 < 0$".
Cho $A,B$ là hai tập hợp được minh họa như hình vẽ bên. Phần không bị gạch trong hình vẽ là tập hợp nào sau đây?
-
A.
$A \cup B$.
-
B.
$A \cap B$.
-
C.
$B\backslash A$.
-
D.
$A\backslash B$.
Miền nghiệm của hệ bất phương trình $\left\{ \begin{array}{l} {3 - y < 0} \\ {2x - 3y + 1 > 0} \end{array} \right.$ chứa điểm nào sau đây?
-
A.
$A\left( {3; 4} \right)$.
-
B.
$B\left( {4; 3} \right)$.
-
C.
$C\left( {7; 4} \right)$.
-
D.
$D\left( {4; 4} \right).$
Bạn Hoa làm một bài thi giữa kỳ I môn Toán. Đề thi gồm 35 câu hỏi trắc nghiệm và 3 câu hỏi tự luận. Khi làm đúng mỗi câu trắc nghiệm được 0,2 điểm, làm đúng mỗi câu tự luận được 1 điểm. Giả sử bạn Hoa làm đúng x câu trắc nghiệm, y câu tự luận. Viết bất phương trình bậc nhất 2 ẩn x, y để đảm bảo bạn Hoa được ít nhất 9 điểm.
-
A.
$x + 0,2y \leq 9.$.
-
B.
$0,2x + y \leq 9$.
-
C.
$0,2x + y \geq 9$.
-
D.
$x + 0,2y > 9$.
Cho tam giác ABC có $\widehat{ABC} = 45^{o}$, $\widehat{ACB} = 60^{o}$ và AB = 3. Tính AC.
-
A.
$AC = \sqrt{6}$.
-
B.
$AC = 3\sqrt{2}$.
-
C.
$AC = 6$.
-
D.
$AC = 2\sqrt{3}$.
Cho $\Delta ABC$ có diện tích $S = 20\sqrt{3}$, chu vi bằng 20. Độ dài bán kính đường tròn nội tiếp r của tam giác ABC là
-
A.
$3$.
-
B.
$2\sqrt{3}$.
-
C.
$\sqrt{3}$.
-
D.
$2$.
Cho tam giác ABC đều. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Cặp vectơ nào sau đây cùng hướng?
-
A.
$\overset{\rightarrow}{MA}$ và $\overset{\rightarrow}{MB}$.
-
B.
$\overset{\rightarrow}{MN}$ và $\overset{\rightarrow}{CB}$.
-
C.
$\overset{\rightarrow}{AB}$ và $\overset{\rightarrow}{MB}$.
-
D.
$\overset{\rightarrow}{AN}$ và $\overset{\rightarrow}{CA}$.
-
A.
$\overset{\rightarrow}{IB} = \dfrac{3}{2}\overset{\rightarrow}{IA}.$
-
B.
$\overset{\rightarrow}{IB} = - \dfrac{3}{5}\overset{\rightarrow}{IA}.$
-
C.
$\overset{\rightarrow}{IB} = \dfrac{3}{5}\overset{\rightarrow}{IA}.$
-
D.
$\overset{\rightarrow}{IB} = - \dfrac{2}{3}\overset{\rightarrow}{IA}.$
Trong mặt phẳng tọa độ Oxy, cho M(4; -1), N(2; 5). Tìm tọa độ trung điểm P của MN.
-
A.
(6; 4).
-
B.
(1; -3).
-
C.
(-1; 3).
-
D.
(3; 2).
Cho tam giác $ABC$ có tọa độ ba đỉnh lần lượt là $A\left( {2;3} \right)$, $B\left( {5;4} \right)$, $C\left( {2;2} \right)$. Tính $\overset{\rightarrow}{AB}.\overset{\rightarrow}{BC}$.
-
A.
$11$.
-
B.
$- 11$.
-
C.
$- 6$.
-
D.
$6$.
Kết quả đo chiều dài một cây cầu có độ chính xác là 0,75 m với dụng cụ đo đảm bảo sai số tương đối không vượt quá 0,15%. Tính độ dài gần đúng của cây cầu.
-
A.
500,1 m.
-
B.
500 m.
-
C.
501 m.
-
D.
499,9 m.
Cho mẫu số liệu dưới dạng bảng tần số như sau:
Tìm số trung bình $\overline{x}$ của mẫu số liệu đã cho.
-
A.
$\overline{x} = 5,1$.
-
B.
$\overline{x} = 18$.
-
C.
$\overline{x} = 3,75$.
-
D.
$\overline{x} = 2,9$.
Trong mặt phẳng với hệ tọa độ Oxy, cho $\Delta ABC$ với A(-2; 5), B(-4; -2), C(1; 5). Các khẳng định sau đây là đúng hay sai?
a) Toạ độ vectơ $\overset{\rightarrow}{u} = 2\overset{\rightarrow}{AB} + \overset{\rightarrow}{AC}$ là (1; 14).
b) Trọng tâm G của tam giác có tọa độ là $\left( {- \dfrac{5}{3}; - \dfrac{8}{3}} \right)$ .
c) Độ dài $AB = \sqrt{53}$ .
d) $\text{cos}\left( {\overset{\rightarrow}{AB},\overset{\rightarrow}{CG}} \right) > 0,8$ với G là trọng tâm của tam giác ABC.
Nhóm bạn Dũng gieo ngẫu nhiên con xúc sắc 100 lần liên tiếp và ghi lại kết quả được thu lại bảng sau:
a) Mốt của mẫu số liệu trên là 6.
b) Số chấm trung bình xuất hiện cho 100 lần gieo là 3,96.
c) Giá trị của tứ phân vị thứ ba là $Q_{3} = 6$.
d) Giá trị trung vị của mẫu số liệu trên là $M_{e} = 4,5$.
Cho các tập hợp \(A = [m - 1;2m + 1)\) và \(B = ( - 2;3)\) với \(A \ne \emptyset \). Có bao nhiêu giá trị nguyên của \(m\) để \(A \subset B\)?
Trong một cuộc đua thuyền ghe được tổ chức trên sông, hai ghe A và B ở vị trí như hình vẽ. Điểm K là vị trí khán giả đứng xem và quan sát thấy ghe A và ghe B theo các góc tạo với bờ IK lần lượt là \({50^o}\) và \({65^o}\). Điểm I là đích đến của cuộc đua, cách K một khoảng 380 mét. Vị trí ghe A, ghe B và đích I nằm trên một đường thẳng tạo với bờ IK một góc bằng \({60^o}\). Tính khoảng cách giữa hai ghe thuyền (đơn vị: mét, làm tròn đến hàng đơn vị).
Gia đình chị Minh dự định trồng rau và hoa trên một mảnh đất có diện tích 8 ha. Nếu trồng 1 ha rau thì cần 20 ngày công và thu lợi 3 triệu đồng. Nếu trồng 1 ha hoa thì cần 30 ngày công và thu lợi 4 triệu đồng. Biết rằng, gia đình chị Minh chỉ có thể sử dụng không quá 180 ngày công cho công việc trồng rau và hoa. Hỏi từ việc trồng rau và hoa nói trên, chị Minh có thể thu về lợi nhuận cao nhất là bao nhiêu triệu đồng?
Ba lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) tác động vào vật M như hình vẽ, làm vật đứng yên. Biết cường độ của các lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) lần lượt là 10 N, 20 N. Tính cường độ của lực \(\overrightarrow {{F_3}} \) (làm tròn kết quả đến hàng phần mười).
Lời giải và đáp án
Mệnh đề phủ định của P: "$\forall x \in \mathbb{R}, x^2 > 0$" là
-
A.
$\overline{P} $: "$\exists x \in \mathbb{R}, x^2 \leq 0$".
-
B.
$\overline{P} $: "$\exists x \in \mathbb{R}, x^2 < 0$".
-
C.
$\overline{P} $: "$\forall x \in \mathbb{R}, x^2 \leq 0$".
-
D.
$\overline{P} $: "$\forall x \in \mathbb{R}, x^2 < 0$".
Đáp án : A
Mệnh đề phủ định của P: "$\forall x \in \mathbb{R}, P(x) > a$" là $\overline P$: "$\exists x \in \mathbb{R}, P(x) \le a$".
Mệnh đề phủ định của P: "$\forall x \in \mathbb{R}, x^2 > 0$" là $\overline P$: "$\exists x \in \mathbb{R}, x^2 \le 0$".
Cho $A,B$ là hai tập hợp được minh họa như hình vẽ bên. Phần không bị gạch trong hình vẽ là tập hợp nào sau đây?
-
A.
$A \cup B$.
-
B.
$A \cap B$.
-
C.
$B\backslash A$.
-
D.
$A\backslash B$.
Đáp án : C
M\N là tập hợp gồm các phần tử thuộc M mà không thuộc N.
Phần không bị gạch là B\A.
Miền nghiệm của hệ bất phương trình $\left\{ \begin{array}{l} {3 - y < 0} \\ {2x - 3y + 1 > 0} \end{array} \right.$ chứa điểm nào sau đây?
-
A.
$A\left( {3; 4} \right)$.
-
B.
$B\left( {4; 3} \right)$.
-
C.
$C\left( {7; 4} \right)$.
-
D.
$D\left( {4; 4} \right).$
Đáp án : C
Thay tọa độ từng điểm vào hệ, nếu thỏa mãn hệ thì điểm đó thuộc miền nghiệm.
Thấy \(\left\{ \begin{array}{l}3 - 4 = - 1 < 0\\2.7 - 3.4 + 1 = 13 > 0\end{array} \right.\) thỏa mãn hệ nên điểm C(7;4) thuộc miền nghiệm của hệ.
Bạn Hoa làm một bài thi giữa kỳ I môn Toán. Đề thi gồm 35 câu hỏi trắc nghiệm và 3 câu hỏi tự luận. Khi làm đúng mỗi câu trắc nghiệm được 0,2 điểm, làm đúng mỗi câu tự luận được 1 điểm. Giả sử bạn Hoa làm đúng x câu trắc nghiệm, y câu tự luận. Viết bất phương trình bậc nhất 2 ẩn x, y để đảm bảo bạn Hoa được ít nhất 9 điểm.
-
A.
$x + 0,2y \leq 9.$.
-
B.
$0,2x + y \leq 9$.
-
C.
$0,2x + y \geq 9$.
-
D.
$x + 0,2y > 9$.
Đáp án : C
Từ giả thiết, lập bất phương trình.
$0,2x + y \geq 9.$
Cho tam giác ABC có $\widehat{ABC} = 45^{o}$, $\widehat{ACB} = 60^{o}$ và AB = 3. Tính AC.
-
A.
$AC = \sqrt{6}$.
-
B.
$AC = 3\sqrt{2}$.
-
C.
$AC = 6$.
-
D.
$AC = 2\sqrt{3}$.
Đáp án : A
Áp dụng định lí sin.
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Leftrightarrow AC = \frac{{AB\sin B}}{{\sin C}} = \frac{{3.\sin {{45}^o}}}{{\sin {{60}^o}}} = \sqrt 6 \).
Cho $\Delta ABC$ có diện tích $S = 20\sqrt{3}$, chu vi bằng 20. Độ dài bán kính đường tròn nội tiếp r của tam giác ABC là
-
A.
$3$.
-
B.
$2\sqrt{3}$.
-
C.
$\sqrt{3}$.
-
D.
$2$.
Đáp án : B
Áp dụng công thức \(S = pr\).
\(S = pr \Leftrightarrow r = \frac{S}{p} = \frac{{20\sqrt 3 }}{{10}} = 2\sqrt 3 \).
Cho tam giác ABC đều. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Cặp vectơ nào sau đây cùng hướng?
-
A.
$\overset{\rightarrow}{MA}$ và $\overset{\rightarrow}{MB}$.
-
B.
$\overset{\rightarrow}{MN}$ và $\overset{\rightarrow}{CB}$.
-
C.
$\overset{\rightarrow}{AB}$ và $\overset{\rightarrow}{MB}$.
-
D.
$\overset{\rightarrow}{AN}$ và $\overset{\rightarrow}{CA}$.
Đáp án : C
Vẽ hình, quan sát và nhận xét.
Ta thấy $\overset{\rightarrow}{AB}$ và $\overset{\rightarrow}{MB}$ cùng hướng.
-
A.
$\overset{\rightarrow}{IB} = \dfrac{3}{2}\overset{\rightarrow}{IA}.$
-
B.
$\overset{\rightarrow}{IB} = - \dfrac{3}{5}\overset{\rightarrow}{IA}.$
-
C.
$\overset{\rightarrow}{IB} = \dfrac{3}{5}\overset{\rightarrow}{IA}.$
-
D.
$\overset{\rightarrow}{IB} = - \dfrac{2}{3}\overset{\rightarrow}{IA}.$
Đáp án : B
Dựa vào tỉ số đoạn thẳng và hướng của hai vecto để xác định.
Ta có \(IB = \frac{3}{5}IA\) và \(\overrightarrow {IB} \) cùng chiều \(\overrightarrow {IA} \) nên \(\overrightarrow {IB} = \frac{3}{5}\overrightarrow {IA} \).
Trong mặt phẳng tọa độ Oxy, cho M(4; -1), N(2; 5). Tìm tọa độ trung điểm P của MN.
-
A.
(6; 4).
-
B.
(1; -3).
-
C.
(-1; 3).
-
D.
(3; 2).
Đáp án : D
Nếu M là trung điểm đoạn thẳng AB thì \({x_M} = \frac{{{x_A} + {x_B}}}{2}\); \({y_M} = \frac{{{y_A} + {y_B}}}{2}\).
\(P = \left( {\frac{{4 + 2}}{2};\frac{{ - 1 + 5}}{2}} \right) = \left( {3;2} \right)\).
Cho tam giác $ABC$ có tọa độ ba đỉnh lần lượt là $A\left( {2;3} \right)$, $B\left( {5;4} \right)$, $C\left( {2;2} \right)$. Tính $\overset{\rightarrow}{AB}.\overset{\rightarrow}{BC}$.
-
A.
$11$.
-
B.
$- 11$.
-
C.
$- 6$.
-
D.
$6$.
Đáp án : B
Áp dụng công thức tính tích vô hướng của hai vecto.
\(\overrightarrow {AB} = (5 - 2;4 - 3) = (3;1)\), \(\overrightarrow {BC} = (2 - 5;2 - 4) = ( - 3; - 2)\).
\(\overrightarrow {AB} .\overrightarrow {BC} = 3.( - 3) + 1.( - 2) = - 11\).
Kết quả đo chiều dài một cây cầu có độ chính xác là 0,75 m với dụng cụ đo đảm bảo sai số tương đối không vượt quá 0,15%. Tính độ dài gần đúng của cây cầu.
-
A.
500,1 m.
-
B.
500 m.
-
C.
501 m.
-
D.
499,9 m.
Đáp án : B
Áp dụng công thức \({\delta _a} \le \frac{d}{{|a|}}\).
Ta có \(0,15\% \le \frac{{0,75}}{{\left| a \right|}} \Leftrightarrow \left| a \right| = 500\).
Cho mẫu số liệu dưới dạng bảng tần số như sau:
Tìm số trung bình $\overline{x}$ của mẫu số liệu đã cho.
-
A.
$\overline{x} = 5,1$.
-
B.
$\overline{x} = 18$.
-
C.
$\overline{x} = 3,75$.
-
D.
$\overline{x} = 2,9$.
Đáp án : A
Áp dụng công thức tính số trung bình: \(\overline x = \frac{{{x_1} + {x_2} + {x_3} + ... + {x_n}}}{n}\).
\(\overline x = \frac{{2.6 + 3.18 + 4.26 + 5.20 + 8.30}}{{6 + 18 + 26 + 20 + 30}} = 5,1\).
Trong mặt phẳng với hệ tọa độ Oxy, cho $\Delta ABC$ với A(-2; 5), B(-4; -2), C(1; 5). Các khẳng định sau đây là đúng hay sai?
a) Toạ độ vectơ $\overset{\rightarrow}{u} = 2\overset{\rightarrow}{AB} + \overset{\rightarrow}{AC}$ là (1; 14).
b) Trọng tâm G của tam giác có tọa độ là $\left( {- \dfrac{5}{3}; - \dfrac{8}{3}} \right)$ .
c) Độ dài $AB = \sqrt{53}$ .
d) $\text{cos}\left( {\overset{\rightarrow}{AB},\overset{\rightarrow}{CG}} \right) > 0,8$ với G là trọng tâm của tam giác ABC.
a) Toạ độ vectơ $\overset{\rightarrow}{u} = 2\overset{\rightarrow}{AB} + \overset{\rightarrow}{AC}$ là (1; 14).
b) Trọng tâm G của tam giác có tọa độ là $\left( {- \dfrac{5}{3}; - \dfrac{8}{3}} \right)$ .
c) Độ dài $AB = \sqrt{53}$ .
d) $\text{cos}\left( {\overset{\rightarrow}{AB},\overset{\rightarrow}{CG}} \right) > 0,8$ với G là trọng tâm của tam giác ABC.
a) \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A}} \right)\).
b) Nếu G là trọng tâm tam giác ABC thì: \({x_M} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\); \({y_M} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\).
c) Nếu \(\overrightarrow a = (x;y)\) thì \(\left| {\overrightarrow a} \right| = \sqrt {\overrightarrow a.\overrightarrow a} = \sqrt {{x^2} + {y^2}} \).
d) Cho \(\overrightarrow u (x;y)\) và \(\overrightarrow v = (x';y')\).
\(\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{\overrightarrow u .\overrightarrow v }}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}} = \frac{{xx' + yy'}}{{\sqrt {{x^2} + {y^2}} .\sqrt {x{'^2} + y{'^2}} }}\).
a) Sai. \(\overrightarrow {AB} = ( - 2; - 7)\), \(\overrightarrow {AC} = (3;0)\). Khi đó:
\(\overrightarrow u = 2\overrightarrow {AB} + \overrightarrow {AC} = \left( { - 2.2 + 3; - 7.2 + 0} \right) = \left( { - 1; - 14} \right)\).
b) Sai. \(G = \left( {\frac{{ - 2 - 4 + 1}}{3};\frac{{5 - 2 + 5}}{3}} \right) = \left( {\frac{{ - 5}}{3};\frac{8}{3}} \right)\).
c) Đúng. \(AB = \sqrt {{{( - 2)}^2} + {{( - 7)}^2}} = \sqrt {53} \).
d) Đúng. \(\overrightarrow {CG} = \left( {\frac{{ - 8}}{3};\frac{{ - 7}}{3}} \right) \Rightarrow CG = \sqrt {{{\left( {\frac{{ - 8}}{3}} \right)}^2} + {{\left( {\frac{{ - 7}}{3}} \right)}^2}} = \frac{{\sqrt {113} }}{3}\).
\({\rm{cos}}\left( {\overrightarrow {AB} ,\overrightarrow {CG} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {CG} }}{{AB.CG}} = \frac{{ - 2.\left( {\frac{{ - 8}}{3}} \right) - 7.\left( {\frac{{ - 7}}{3}} \right)}}{{\sqrt {53} .\frac{{\sqrt {113} }}{3}}} \approx 0,84\).
Nhóm bạn Dũng gieo ngẫu nhiên con xúc sắc 100 lần liên tiếp và ghi lại kết quả được thu lại bảng sau:
a) Mốt của mẫu số liệu trên là 6.
b) Số chấm trung bình xuất hiện cho 100 lần gieo là 3,96.
c) Giá trị của tứ phân vị thứ ba là $Q_{3} = 6$.
d) Giá trị trung vị của mẫu số liệu trên là $M_{e} = 4,5$.
a) Mốt của mẫu số liệu trên là 6.
b) Số chấm trung bình xuất hiện cho 100 lần gieo là 3,96.
c) Giá trị của tứ phân vị thứ ba là $Q_{3} = 6$.
d) Giá trị trung vị của mẫu số liệu trên là $M_{e} = 4,5$.
Cho mẫu số liệu \({x_1},{x_2},{x_3},...,{x_n}\).
+) Mốt của mẫu số liệu là giá trị xuất hiện với tần số lớn nhất, kí hiệu: \({M_e}\).
+) Số trung bình (hay TB cộng) của mẫu số liệu kí hiệu là \(\overline x \), được tính bằng công thức:
\(\overline x = \frac{{{x_1} + {x_2} + {x_3} + ... + {x_n}}}{n}\).
+) Để tìm các tứ phân vị của mẫu số liệu có n giá trị, ta làm như sau:
- Sắp xếp mẫu số liệu theo thứ tự không giảm.
- Tìm trung vị. Giá trị này là $Q_2$.
- Tìm trung vị của nửa số liệu bên trái $Q_2$ (không bao gồm $Q_2$ nếu n lẻ). Giá trị này là $Q_1$, được gọi là tứ phân vị thứ nhất hay tứ phân vị dưới.
- Tìm trung vị của nửa số liệu bên phải $Q_2$ (không bao gồm $Q_2$ nếu n lẻ). Giá trị này là $Q_3$, được gọi là tứ phân vị thứ ba hay tứ phân vị trên.
Gọi \({x_1};{x_2};...;{x_{100}}\) lần lượt là số chấm của 100 lần gieo xúc xắc được sắp xếp theo giá trị từ nhỏ đến lớn.
a) Đúng. Mốt của mẫu số liệu trên là 6 vì 6 có tần số lớn nhất.
b) Sai. \(\overline x = \frac{{1.14 + 2.16 + 3.18 + 4.8 + 5.10 + 6.34}}{{100}} = 3,86\).
c) Đúng. \({Q_3} = \frac{{{x_{75}} + {x_{76}}}}{2} = \frac{{6 + 6}}{2} = 6\).
d) Sai. \({M_e} = \frac{{{x_{50}} + {x_{51}}}}{2} = \frac{{4 + 4}}{2} = 4\).
Cho các tập hợp \(A = [m - 1;2m + 1)\) và \(B = ( - 2;3)\) với \(A \ne \emptyset \). Có bao nhiêu giá trị nguyên của \(m\) để \(A \subset B\)?
\(A \subset B\) khi và chỉ khi mọi phần tử thuộc A đều thuộc B.
Điều kiện: \(m - 1 < 2m + 1 \Leftrightarrow m > - 2\).
Để \(A \subset B\) thì: \(\left\{ {\begin{array}{*{20}{l}}{ - 2 < m - 1}\\{2m + 1 \le 3}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{m > - 1}\\{m \le 1}\end{array}} \right. \Rightarrow - 1 < m \le 1.\)
So sánh với điều kiện ta được \( - 1 < m \le 1\). Mà \(m \in \mathbb{Z} \Rightarrow m \in \{ 0;1\} \).
Vậy có 2 giá trị nguyên của \(m\) để \(A \subset B\).
Trong một cuộc đua thuyền ghe được tổ chức trên sông, hai ghe A và B ở vị trí như hình vẽ. Điểm K là vị trí khán giả đứng xem và quan sát thấy ghe A và ghe B theo các góc tạo với bờ IK lần lượt là \({50^o}\) và \({65^o}\). Điểm I là đích đến của cuộc đua, cách K một khoảng 380 mét. Vị trí ghe A, ghe B và đích I nằm trên một đường thẳng tạo với bờ IK một góc bằng \({60^o}\). Tính khoảng cách giữa hai ghe thuyền (đơn vị: mét, làm tròn đến hàng đơn vị).
Áp dụng định lí sin.
Trong tam giác AKI ta có:
\(\widehat {IAK} = {180^o} - \widehat {AIK} - \widehat {AKI} = {180^o} - {60^o} - {50^o} = {70^o}\).
Áp dụng định lí sin vào tam giác AKI ta có: \(\frac{{AK}}{{\sin AIK}} = \frac{{IK}}{{\sin KAI}} \Rightarrow AK = \frac{{IK \cdot \sin AIK}}{{\sin KAI}} = \frac{{380 \cdot \sin {{60}^o}}}{{\sin {{70}^o}}} \approx 350,21\) (m).
Lại có: \(\widehat {KAB} = {180^o} - \widehat {KAI} = {180^o} - {70^o} = {110^o}\).
Áp dụng định lí sin vào tam giác AKB ta có: \(\frac{{AB}}{{\sin AKB}} = \frac{{AK}}{{\sin ABK}} \)
\(\Rightarrow AB = \frac{{AK \cdot \sin AKB}}{{\sin ABK}} \approx \frac{{350,21 \cdot \sin ({{65}^o} - {{50}^o})}}{{\sin ({{180}^o} - {{110}^o} - {{15}^o})}} \approx 111\) (m).
Gia đình chị Minh dự định trồng rau và hoa trên một mảnh đất có diện tích 8 ha. Nếu trồng 1 ha rau thì cần 20 ngày công và thu lợi 3 triệu đồng. Nếu trồng 1 ha hoa thì cần 30 ngày công và thu lợi 4 triệu đồng. Biết rằng, gia đình chị Minh chỉ có thể sử dụng không quá 180 ngày công cho công việc trồng rau và hoa. Hỏi từ việc trồng rau và hoa nói trên, chị Minh có thể thu về lợi nhuận cao nhất là bao nhiêu triệu đồng?
Ứng dụng hệ bất phương trình bậc nhất hai ẩn để giải.
Gọi x, y \((x \ge 0,y \ge 0)\) lần lượt là số ha đất trồng rau và hoa.
Diện tích đất trồng canh tác không vượt quá 8 ha nên ta có: \(x + y \le 8\).
Số ngày công sử dụng không vượt quá 180 ngày nên \(20x + 30y \le 180\).
Từ đó, ta có hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x \ge 0}\\{y \ge 0}\\{x + y \le 8}\\{20x + 30y \le 180}\end{array}} \right.\)
Ta cần tìm x, y sao cho T(x, y) = 3x + 4y lớn nhất.
Miền nghiệm của hệ được biểu diễn như sau:
Miền nghiệm của hệ bất phương trình trên là miền trong của tứ giác OABC, kể cả 4 cạnh của tứ giác đó, với O(0;0), A(8;0), B(6;2), C(0;6).
Tại O(0;0), ta có: T = 3.0 + 4.0 = 0;
Tại A(8;0), ta có: T = 3.8 + 4.0 = 24;
Tại B(6;2), ta có: T = 3.6 + 4.2 = 26;
Tại C(0;6), ta có: T = 3.0 + 4.6 = 24.
Vậy số lợi nhuận cao nhất mà gia đình chị Minh thu được từ trồng rau và hoa là 26 triệu đồng.
Ba lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) tác động vào vật M như hình vẽ, làm vật đứng yên. Biết cường độ của các lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) lần lượt là 10 N, 20 N. Tính cường độ của lực \(\overrightarrow {{F_3}} \) (làm tròn kết quả đến hàng phần mười).
Áp dụng quy tắc hình bình hành và định lí cos.
Gọi A, B, C là điểm cuối của các vectơ lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) và dựng hình bình hành MADB.
Gọi \(\overrightarrow {{F_{12}}} \) là hợp lực của hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \).
Ta có \(\widehat {MBD} = {180^o} - \widehat {AMB} = {120^o}\). \(MB = \left| {\overrightarrow {{F_2}} } \right| = 20\), \(BD = MA = \left| {\overrightarrow {{F_1}} } \right| = 10\).
\(\left| {\overrightarrow {{F_{12}}} } \right| = MD = \sqrt {M{B^2} + B{D^2} - 2.MB.BD.\cos MBD} = 10\sqrt 7 \) (N).
Vật đứng yên nên \(\overrightarrow {{F_3}} = - \overrightarrow {{F_{12}}} \Rightarrow \left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {{F_{12}}} } \right| = 10\sqrt 7 \approx 26,5\) (N).
Bước 1: Xác định hướng, độ lớn của các vecto vận tốc.
Bước 2: Từ giả thiết “vật đứng yên” suy ra cường độ và hướng của lực \(\overrightarrow {{F_3}} \).
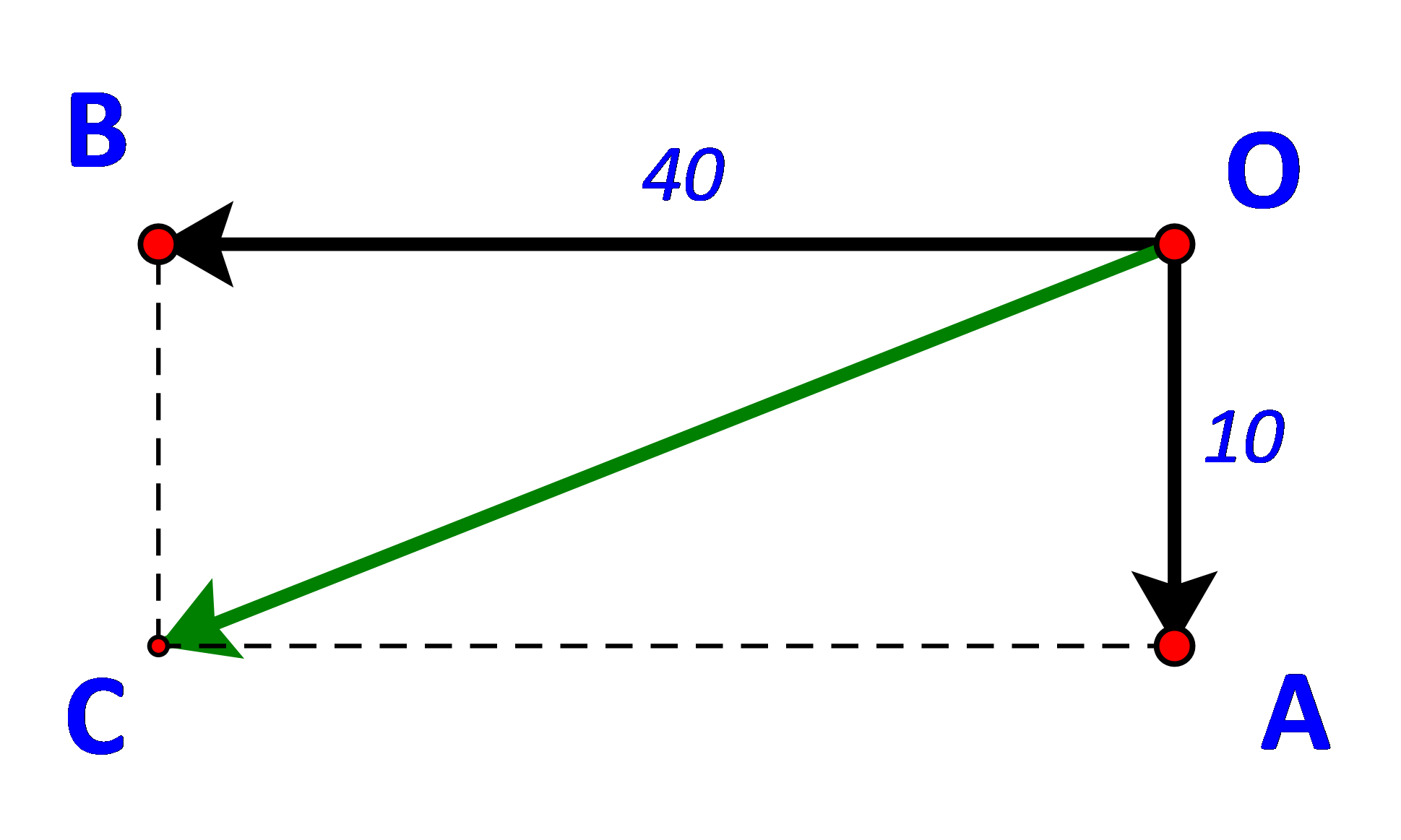
Gọi O là vị trí của ca nô.
Vẽ \(\overrightarrow {OA} \) là vận tốc dòng nước (chảy từ phía bắc xuống phía nam);
\(\overrightarrow {OB} \) là vận tốc riêng của ca nô (chuyển động từ phía đông sang phía tây).
Khi đó vecto vận tốc của ca nô so với bờ sông là vecto \(\overrightarrow {OA} + \overrightarrow {OB} \).
Gọi C là đỉnh thứ tư của hình bình hành OACB, ta có: \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \)
Xét tam giác OBC vuông tại B ta có:
BC = 40; BC = OA = 10.
\( \Rightarrow OC = \sqrt {O{B^2} + B{C^2}} = 10\sqrt {17} \).
Vậy vận tốc của ca nô so với bờ sông là \(10\sqrt {17} \) km/h.
Gọi C là địa điểm máy bay đến sau khi xuất phát 1 giờ. Tìm tọa độ điểm C.
Bước 1: Tính tọa độ \(\overrightarrow {AB} \).
Bước 2: Từ giả thiết tìm điểm C thỏa mãn \(\overrightarrow {AC} = \frac{1}{3}\overrightarrow {AB} \) rồi kết luận.
Gọi C(a; b) là địa điểm máy bay đến sau khi xuất phát 1 giờ.
Ta có: \(\overrightarrow {AB} = ( - 400;300)\).
Theo giả thiết, AC = \(\frac{1}{3}AB\) \( \Rightarrow \overrightarrow {AC} = \frac{1}{3}\overrightarrow {AB} \Leftrightarrow \left\{ \begin{array}{l}a - 600 = \frac{1}{3}.( - 400)\\b - 200 = \frac{1}{3}.300\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{1400}}{3}\\b = 300\end{array} \right. \Rightarrow C\left( {\frac{{1400}}{3};300} \right)\).
Vậy toạ độ của máy bay trực thăng tại thời điểm sau khi xuất phát 1 giờ là \(\left( {\frac{{1400}}{3};300} \right)\).
Áp dụng công thức \(s = \sqrt {{s^2}} \), trong đó:
\({s^2} = \frac{{{{({x_1} - \bar x)}^2} + {{({x_2} - \bar x)}^2} + \cdots + {{({x_n} - \bar x)}^2}}}{n}\)
\(= \frac{1}{n}({n_1}{x_1}^2 + {n_2}{x_2}^2 + ... + {n_k}{x_k}^2) - {\overline x ^2}\).
+) Ta có bàng tần số:
+) Từ bảng tần số ta có số lượng áo trung bình bán ra trong 1 tháng là: \(\overline x = 575\) ( chiếc áo).
+) Phương sai của mẫu số liệu là:
\({s^2} \)
\(= \frac{{{{\left( {410 - \overline x } \right)}^2} + {{\left( {430 - \overline x } \right)}^2} + {{\left( {450 - \overline x } \right)}^2} + {{\left( {525 - \overline x } \right)}^2} + {{\left( {550 - \overline x } \right)}^2} + {{\left( {560 - \overline x } \right)}^2} + {{\left( {635 - \overline x } \right)}^2} + {{\left( {760 - \overline x } \right)}^2} + {{\left( {800 - \overline x } \right)}^2} + {{\left( {900 - \overline x } \right)}^2}}}{{12}}\)
\(= 25401\).
+) Độ lệch chuẩn của mẫu số liệu là: \(s = \sqrt {{s^2}} = 159,4\).
Đề thi học kì 1 Toán 10 Kết nối tri thức - Đề số 14
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
Câu 1: Trong các mệnh đề sau, mệnh đề nào đúng? A. (forall x in mathbb{R},,x le {x^2}) B. (forall x in mathbb{R},,,left| x right| < 3 Leftrightarrow x < 3) C. (forall n in mathbb{N},,,{n^2} + 1)chia hết cho 3 D. (exists a in mathbb{Q},,{a^2} = 2)
Câu 1: Trong các câu sau, có bao nhiêu câu là mệnh đề? a) Cố lên, sắp đói rồi! b) Số 15 là số nguyên tố. c) Tổng các góc của một tam giác là (180^circ .) d) (x) là số nguyên dương.
Câu 1: Trong các câu sau đâu là mệnh đề chứa biến? A. 2 là số nguyên tố. B. 17 là số chẵn C. x + y > 0 D. Hình vuông có hai đường chéo vuông góc
Câu 1: Phát biểu nào sau đây là một mệnh đề? A. Mùa thu Hà Nội đẹp quá! B. Bạn có đi học không? C. Đề thi môn Toán khó quá! D. Hà Nội là thủ đô của Việt Nam.
Câu 1: Trong các câu sau, có bao nhiêu câu là không phải là mệnh đề? a) Huế là một thành phố của Việt Nam. b) Sông Hương chảy ngang qua thành phố Huế. c) Hãy trả lời câu hỏi này! d) 5 + 19 = 24. e) 6 + 81 = 25. f) Bạn có mang theo máy tính không? g) x + 2 = 11.
Câu 1: Mệnh đề nào sau đây sai? A. Tam giác có hai góc bằng nhau thì góc thứ ba bằng nhau B. Hai tam giác bằng nhau thì có diện tích bằng nhau C. Tam giác có ba cạnh bằng nhau thì có ba góc bằng nhau D. Hai tam giác có diện bằng nhau thì bằng nhau.
Câu 1: Trong các câu sau, có bao nhiêu câu là mệnh đề? a) Hãy đi nhanh lên! b) Hà Nội là thủ đô của Việt Nam. c) (5 + 7 + 4 = 15) d) Năm 2018 là năm nhuận.
Câu 1: Cho các phát biểu sau đây: (1) “17 là số nguyên tố”. (2) “Tam giác vuông có một đường trung tuyến bằng nửa cạnh huyền”. (3) “Các em C14 hãy cố gắng học tập thật tốt nhé!” (4) “Mọi hình chữ nhật đều nội tiếp được đường tròn”. Hỏi có bao nhiêu phát biểu là mệnh đề?
Câu 1: Cho các câu sau: (1) Số 7 là số lẻ. (2) Bài toán này khó quá! (3) Cuối tuần này bạn có rảnh không? (4) Số 10 là một số nguyên tố. Trong các câu trên có bao nhiêu câu là mệnh đề?
Câu 1: Câu nào sau đây không phải là mênh đề? A. Bạn bao nhiêu tuổi? B. Hôm nay là chủ nhật. C. Trái đất hình tròn. D. 4 ne 5. Câu 2: Cho số (bar a = 31975421 pm 150). Hãy viết số quy tròn của số 31975421. A. 31975400. B. 31976000. C. 31970000. D. 31975000.
A. Nội dung ôn tập Mệnh đề và tập hợp 1. Mệnh đề 2. Tập hợp và các phép toán trên tập hợp Bất phương trình và hệ bất phương trình bậc nhất hai ẩn 1. Bất phương trình bậc nhất hai ẩn 2. Hệ bất phương trình bậc nhất hai ẩn Hệ thức lượng trong tam giác 1. Giá trị lượng giác của một góc từ đến 2. Hệ thức lượng trong tam giác
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
