-
PHẦN ĐẠI SỐ VÀ GIẢI TÍCH
-
PHẦN HÌNH HỌC
-
100 bài tập khoảng cách
50 bài tập đại cương về đường thẳng và mặt phẳng mức độ nhận biết, thông hiểu
Làm đề thiCâu hỏi 1 :
Có bao nhiêu cách xác định một mặt phẳng:
- A 2
- B 3
- C 4
- D 1
Đáp án: C
Phương pháp giải:
Nhớ lại các kiến thức về cách xác định một mặt phẳng.
Lời giải chi tiết:
- Qua 3 điểm phân biệt không thẳng hàng xác định một mặt phẳng duy nhất.
- Qua hai đường thẳng cắt nhau xác định một mặt phẳng duy nhất.
- Qua một đường thẳng và một điểm nằm ngoài đường thẳng đó xác định một mặt phẳng duy nhất.
- Qua 2 đường thẳng song song xác định một mặt phẳng duy nhất.
Vậy có 4 cách.
Chọn C.
Câu hỏi 2 :
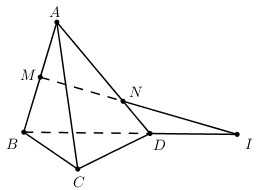
Cho tứ diện ABCD. Trên cạnh AB, AC lấy các điểm M, N sao cho MN cắt BC tại E và O là điểm bất kì trong tam giác BCD. Giao tuyến của (OMN) và (BCD) là:
- A OC
- B OB
- C OD
- D OE
Đáp án: D
Phương pháp giải:
Xác định giao tuyến của hai mặt phẳng bằng cách xác định 2 điểm chung của mặt phẳng đó.
Lời giải chi tiết:
Ta có: \(E = MN \cap BC \Rightarrow \left\{ \begin{array}{l}E \in MN \subset \left( {OMN} \right)\\E \in BC \subset \left( {BCD} \right)\end{array} \right. \Rightarrow E \in \left( {OMN} \right) \cap \left( {BCD} \right)\)
Và \(O\in \left( OMN \right)\cap \left( BCD \right)\).
Vậy \(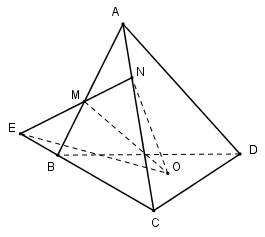
OE=\left( OMN \right)\cap \left( BCD \right)\)
Chọn D.
Câu hỏi 3 :
Trong các mệnh đề sau, mệnh đề nào sai?
- A Có một và chỉ một mặt phẳng đi qua 3 điểm phân biệt không thẳng hàng cho trước.
- B Có một và chỉ một mặt phẳng đi qua 2 đường thẳng cắt nhau.
- C Có một và chỉ một mặt phẳng đi qua 1 đường thẳng và 1 điểm nằm ngoài đường thẳng đó.
- D Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung nữa.
Đáp án: D
Phương pháp giải:
Nhớ lại các kiến thức về cách xác định một mặt phẳng.
Lời giải chi tiết:
Có 4 cách xác định một mặt phẳng:
- Qua 3 điểm phân biệt không thẳng hàng xác định một mặt phẳng duy nhất.
- Qua hai đường thẳng cắt nhau xác định một mặt phẳng duy nhất.
- Qua một đường thẳng và một điểm nằm ngoài đường thẳng đó xác định một mặt phẳng duy nhất.
- Qua 2 đường thẳng song song xác định một mặt phẳng duy nhất.
D sai vì hai mặt phẳng phân biệt có 1 điểm chung sẽ cắt nhau theo giao tuyến là 1 đường thẳng. Chính vì vậy chúng có vô số điểm chung nữa.
Chọn D.
Câu hỏi 4 :
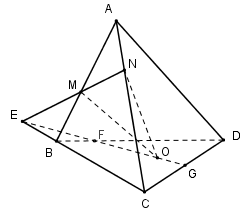
Cho tứ diện ABCD. Trên cạnh AB, AC lấy các điểm M, N sao cho MN cắt BC tại E và O là điểm bất kì trong tam giác BCD. Kết luận nào sau đây đúng ?
(I) Giao điểm của (OMN) và BC là điểm E.
(II) Giao điểm của (OMN) và BD là giao điểm của BD và OE.
(III) Giao điểm của (OMN) và CD là giao điểm của CD và ON.
- A Cả ba đều đúng
- B Chỉ có (I) đúng.
- C Chỉ có (I) và (II) đúng
- D Chỉ có (I) và (III) đúng
Đáp án: C
Phương pháp giải:
Suy luận từng đáp án dựa vào giao điểm của đường thẳng và mặt phẳng.
Lời giải chi tiết:
\(E\in BC,E\in MN\subset \left( OMN \right)\Rightarrow E=BC\cap \left( OMN \right)\Rightarrow \)(I) đúng.
Trong (BCD) gọi \(F=OE\cap BD\Rightarrow F=BD\cap \left( OMN \right)\Rightarrow \)(II) đúng.
Trong (BCD) gọi \(G=OE\cap CD\Rightarrow G=\left( OMN \right)\cap CD\Rightarrow \) (III) sai.
Chọn C.
Câu hỏi 5 :
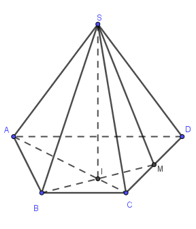
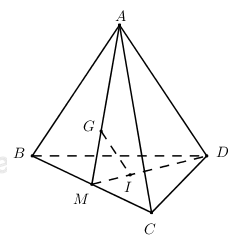
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M là trung điểm của SC. Giao điểm I của AM và (SBD) là:
- A Giao điểm của AM và SO
- B Giao điểm của AM và SD
- C Giao điểm của AM và SB
- D Giao điểm của AM và BD.
Đáp án: A
Phương pháp giải:
Đưa về cùng mặt phẳng để tìm giao điểm.
Lời giải chi tiết:
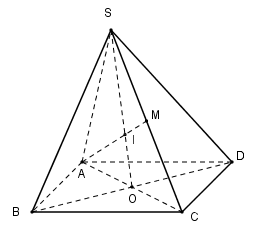
Xét trong (SAC) có \(AM\cap SO=I\).
Mà \(SO\subset \left( SBD \right)\Rightarrow AM\cap \left( SBD \right)=I.\)
Chọn A.
Câu hỏi 6 :
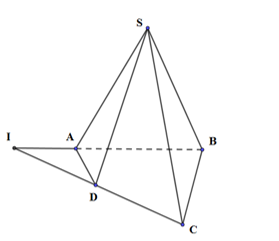
Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi với AB và CD không song song. Gọi I là giao điểm của 2 đường thẳng AB và CD. Gọi d là giao tuyến các mặt (SAB) và (SCD). Tìm d ?
- A \(d\equiv SO\)
- B \(d\equiv AC\)
- C \(d\equiv BD\)
- D \(d\equiv SI\)
Đáp án: D
Phương pháp giải:
Tìm giao tuyến của hai mặt phẳng ta đi tìm 2 điểm chung của 2 mặt phẳng đó.
Lời giải chi tiết:
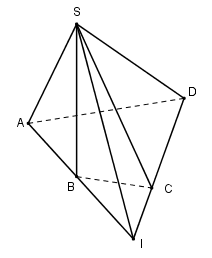
Gọi \(I=AB\cap CD\) ta có:
\(\begin{array}{l}I \in AB \Rightarrow I \in \left( {SAB} \right),I \in CD \Rightarrow I \in \left( {SCD} \right)\\S \in \left( {SAB} \right) \cap \left( {SCD} \right)\\ \Rightarrow \left( {SAB} \right) \cap \left( {SCD} \right) = SI \Rightarrow d \equiv SI\end{array}\)
Chọn D.
Câu hỏi 7 :
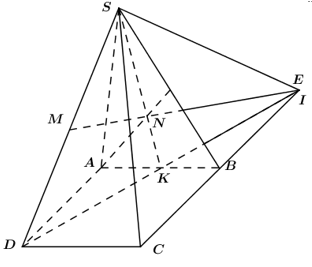
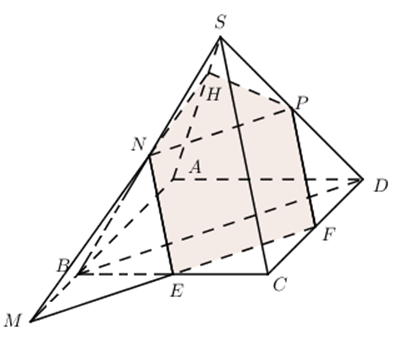
Cho hình bình hành ABCD nằm trong mặt phẳng (P) và một điểm S nằm ngoài mặt phẳng (P). Gọi M là điểm nằm giữa S và A; N là điểm nằm giữa S và B; giao điểm của hai đường thẳng AC và BD là O; giao điểm của hai đường thẳng CM và SO là I; giao điểm của hai đường thẳng NI và SD là J. Tìm giao điểm của mp(CMN) với đường thẳng SO là:
- A A
- B J
- C I
- D B
Đáp án: C
Phương pháp giải:
Tìm trong mặt phẳng (CMN) một đường thẳng cắt SO. Giao điểm của đường thẳng đó và SO chính là giao điểm của (CMN) và SO.
Lời giải chi tiết:
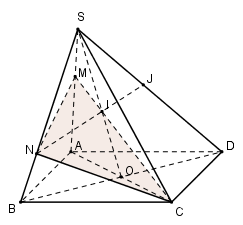
Dễ thấy trong (SAC) có \)SO\cap CM=I.\)Mà \(CM\subset \left( CMN \right)\Rightarrow SO\cap \left( CMN \right)=I.\)
Chọn C.
Câu hỏi 8 :
Cho hình chóp S.ABCD như hình vẽ bên dưới. CÓ ABCD là tứ giác lồi. Với W là điểm thuộc cạnh SD, X là giao điểm của hai đường thẳng AC với BD và Y là giao điểm 2 đường thẳng SX với BW. Gọi P là giao điểm của DY và (SAB). Khẳng định nào dưới đây đúng?
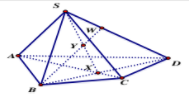
- A P là giao điểm của 2 đường thẳng DY và SB
- B P là giao điểm của 2 đường thẳng DY và SA
- C P là giao điểm của 2 đường thẳng DY và AB
- D P là giao điểm của 2 đường thẳng DW và SC
Đáp án: A
Phương pháp giải:
Đưa về cùng mặt phẳng. Tìm trong mặt phẳng (ABC) một đường thẳng cắt MG. Giao điểm của đường thẳng đó và SO chính là giao điểm của (ABC) và MG.
Lời giải chi tiết:
Trong (SBD) gọi \(P=DY\cap SB.\) Mà \(SB\subset \left( SBD \right)\Rightarrow DY\cap \left( SBD \right)=P.\)
Chọn A.
Câu hỏi 9 :
Số phần tử của tập hợp các điểm chung của một đường thẳng và một mặt phẳng không thể là:
- A 0
- B 1
- C 2
- D Vô số
Đáp án: C
Phương pháp giải:
Dựa vào các vị trí tương đối giữa đường thẳng và mặt phẳng.
Lời giải chi tiết:
Chỉ có 3 vị trí tương đối của đường thẳng và mặt phẳng:
Nếu đường thẳng song song với mặt phẳng thì số điểm chung là giữa chúng là 0
Nếu đường thẳng cắt mặt phẳng tại 1 điểm duy nhất thì số điểm chúng là 1
Nếu đường thẳng nằm trong mặt phẳng thì giữa chúng có vô số điểm chung.
Chọn đáp án C
Câu hỏi 10 :
Cho hình chóp S.ABCD có đáy là đa giác lồi, O là giao điểm của AC và BD, B’, C’ lần lượt là trung điểm của SB, SC. SD cắt (AB’C’) tại D’. Khi đó:
- A Các đường thẳng AC’, B’D’, SO đồng quy
- B B’, C’, D’ thẳng hàng.
- C Các đường thẳng AC’, B’D’, SO đồng phẳng .
- D S, O, D’ thẳng hàng.
Đáp án: A
Phương pháp giải:
Giao tuyến của 3 mặt phẳng phân biệt hoặc song song, hoặc đồng quy.
Lời giải chi tiết:
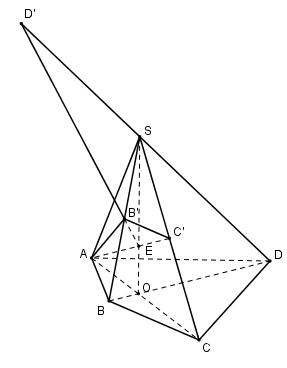
Trong (SAC) gọi \(E=SO\cap AC'\Rightarrow E\in \left( AB'C' \right)\Rightarrow B'E\subset \left( AB'C' \right)\)
Trong (SBD) gọi \(D'=B'E\cap SD.\) Mà \(B'E\subset \left( AB'C' \right)\Rightarrow SD\cap \left( AB'C' \right)=D'.\)
Ta có: \(\left\{ \begin{array}{l}\left( {AB'C'} \right) \cap \left( {SAC} \right) = AC'\\\left( {AB'C'} \right) \cap \left( {SBD} \right) = B'D'\\\left( {SAC} \right) \cap \left( {SBD} \right) = SO\end{array} \right. \Rightarrow \) Các đường thẳng AC’, B’D’, SO đồng quy hoặc song song.
Mà \(AC'\cap SO=E\) nên các đường thẳng AC’, B’D’, SO đồng quy tại E.
Chọn A.
Câu hỏi 11 :
Một mặt phẳng xác định bởi:
- A Hai đường thẳng chéo nhau.
- B Hai đường thẳng không song song.
- C Ba điểm phân biệt.
- D Một điểm và một đường thẳng không đi qua điểm đó.
Đáp án: D
Phương pháp giải:
Có 4 cách xác định một mặt phẳng:
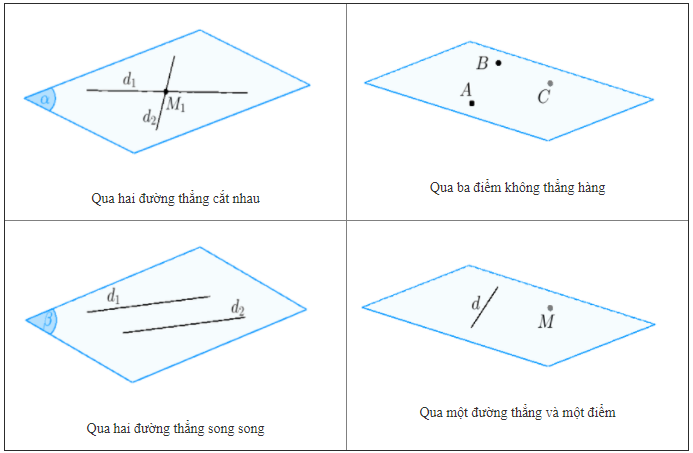
Lời giải chi tiết:
Dựa vào các cách xác định một mặt phẳng ta thấy chỉ có đáp án D đúng.
Chọn D.
Câu hỏi 12 :
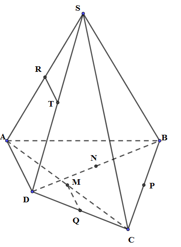
Cho hình chóp S.ABC có ABC là tam giác. Gọi M, N lần lượt là hai điểm thuộc cạnh AC, BC sao cho MN không song song với AB. Gọi đường thẳng a là giao tuyến của (SMN) và (SAB). Tìm a?
- A \(a\equiv SQ\) với Q là giao điểm của BH với MN, H là điểm thuộc SA.
- B \(a\equiv MI\) với I là giao điểm của hai đường thẳng MN và AB.
- C \(a\equiv SO\) với O là giao điểm của hai đường thẳng AM và BN
- D \(a\equiv SI\) với I là giao điểm của hai đường thẳng MN và AB.
Đáp án: D
Phương pháp giải:
Tìm giao tuyến của hai mặt phẳng ta đi tìm 2 điểm chung của 2 mặt phẳng đó.
Lời giải chi tiết:
Gọi
\(\begin{array}{l}I = MN \cap AB\\I \in MN \Rightarrow I \in \left( {SMN} \right),I \in AB \Rightarrow I \in \left( {SAB} \right)\\ \Rightarrow I = \left( {SAB} \right) \cap \left( {SMN} \right)\\S \in \left( {SAB} \right) \cap \left( {SMN} \right)\\ \Rightarrow \left( {SAB} \right) \cap \left( {SMN} \right) = SI.\end{array}\)
Chọn D.
Câu hỏi 13 :
Giả sử M là giao của đường thẳng a và mặt phẳng (P). Khẳng định nào sau đây sai?
- A \(M \in a\)
- B \(M \in \left( P \right)\)
- C Tồn tại đường thẳng \(b \subset \left( P \right)\) sao cho M là giao điểm của a và b
- D Với đường thẳng b bất kỳ nằm trong (P), ta có M là giao của a và b
Đáp án: D
Phương pháp giải:
Dựa vào vị trí tương đối đường thẳng cắt mặt phẳng.
Lời giải chi tiết:
Khi M là giao điểm của đường thẳng a và mặt phẳng (P) thì M ∈ a và \(M \in \left( P \right)\) và tồn tại đường thẳng b ⊂ (P) đi qua M, do đó M là giao điểm của a và b
Chọn đáp án D
Câu hỏi 14 :
Cho hình chóp S.ABC. M, N lần lượt nằm trên 2 cạnh SA, SB sao cho MN không song song với AB. Khi đó giao điểm của MN và mặt phẳng (ABC) là:
- A Giao của MN và AC
- B Giao của MN và BC
- C Giao của MN và AB
- D Đáp án khác
Đáp án: C
Phương pháp giải:
+ Tìm một mặt phẳng thích hợp chứa MN
+ Tìm giao tuyến của mặt phẳng đó với (ABC)
+ Tìm giao điểm của giao tuyến đó với MN
Lời giải chi tiết:
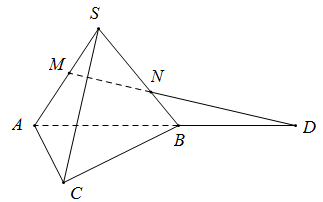
Ta có MN ⊂ (SAB)
(SAB) ∩ (ABC) = AB
Gọi D là giao điểm của MN và AB
⇒ D là giao điểm của MN và (ABC)
Chọn đáp án C
Câu hỏi 15 :
Hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến là đường thẳng d. Hai đường thẳng a, b lần lượt nằm trong (α), (β) và đều cắt đường thẳng d. Khẳng định nào sau đây sai?
- A Giao điểm của a và d là giao điểm của a và mặt phẳng (β)
- B Giao điểm của b và d là giao điểm của b và mặt phẳng (α)
- C Giao điểm của b và mặt phẳng (α) nằm ngoài đường thẳng d
- D Giao điểm của a và mặt phẳng (β) luôn nằm trên đường thẳng d
Đáp án: C
Phương pháp giải:
Ta tìm giao tuyến của đường thẳng b và mặt phẳng (α):
+ Tìm một mặt phẳng chứa b thích hợp
+ Tìm giao tuyến của mặt phẳng này với mặt phẳng (α)
+ Tìm giao điểm của giao tuyến đó với đường thẳng b
Lời giải chi tiết:
+ Ta có (β) là mặt phẳng chứa đường thẳng b
+ Giao tuyến của (β) và (α) là d
+ Giao điểm của d và b là M
⇒ M là giao điểm của b và (α)
Vậy M nằm trên đường thẳng d
Chọn đáp án C
Câu hỏi 16 :
Cho tứ diện \(ABCD\) và ba điểm \(M,\,N,\,P\) lần lượt nằm trên các cạnh \(AB,\,AC,\,AD\) mà không trùng với các đỉnh của tứ diện. Thiết diện của hình tứ diện \(ABCD\) khi cắt bởi mặt phẳng \(\left( {MNP} \right)\) là:
- A Một tam giác
- B Một ngũ giác
- C Một đoạn thẳng
- D Một tứ giác
Đáp án: A
Phương pháp giải:
Vẽ hình để thấy thiết diện.
Lời giải chi tiết:
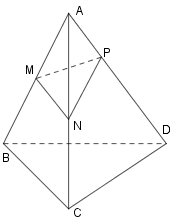
Thiết diện của tứ diện \(ABCD\) khi cắt bởi mặt phẳng \(\left( {MNP} \right)\) chính là tam giác \(MNP.\)
Chọn A.
Câu hỏi 17 :
Cho hình lăng trụ ABC.A’B’C’. Cắt hình lăng trụ bởi một mặt phẳng ta được một thiết diện. Số cạnh lớn nhất của thiết diện thu được là?
- A 4
- B 5
- C 3
- D 6
Đáp án: A
Lời giải chi tiết:
Chọn A.
Câu hỏi 18 :
Cho hình chóp \(S.ABCD\) có đáy là hình thang \(ABCD\,\left( {AD//BC} \right)\). Gọi \(M\)là trung điểm của \(CD\). Giao tuyến của hai mặt phẳng \(\left( {MSB} \right)\) và \(\left( {SAC} \right)\)là:
- A \(SP\) (\(P\)là giao điểm của\(AB\) và \(CD\)).
- B \(SO\) (\(O\) là giao điểm của\(AC\) và \(BD\)).
- C \(SJ\) (\(J\)là giao điểm của\(AM\) và \(BD\)).
- D \(SI\) (\(I\) là giao điểm của\(AC\) và \(BM\)).
Đáp án: D
Phương pháp giải:
Xác định 2 điểm phân biệt cùng thuộc cả hai mặt phẳng cần xét.
Lời giải chi tiết:
Trong \(\left( {ABCD} \right)\), gọi \(I\) là giao điểm của\(AC\) và \(BM\)
Khi đó: \(\left\{ \begin{array}{l}I \in AC \subset \left( {SAC} \right)\\I \in BM \subset \left( {SBM} \right)\end{array} \right. \Rightarrow I \in \left( {SAC} \right) \cap \left( {SBM} \right)\)
Mà \(S \in \left( {SAC} \right) \cap \left( {SBM} \right) \Rightarrow \left( {SAC} \right) \cap \left( {SBM} \right) = SI\).
Chọn: D
Câu hỏi 19 :
Cho điểm A, đường thẳng d và mặt phẳng (P). Ký hiệu nào sau đây đúng?
- A \(A \subset d\).
- B \(A \not\subset \left( P \right)\).
- C \(d \subset \left( P \right)\).
- D \(d \notin \left( P \right)\).
Đáp án: C
Lời giải chi tiết:
Ký hiệu đúng là: \(d \subset \left( P \right)\).
Chọn: C
Câu hỏi 20 :
Mệnh đề nào sau đây sai?
- A Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
- B Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa.
- C Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.
- D Nếu ba điểm phân biệt cùng thuộc hai mặt phẳng phân biệt thì chúng thẳng hàng.
Đáp án: A
Lời giải chi tiết:
Mệnh đề sai là: Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất. (do hai mặt phẳng đó có thể trùng nhau).
Chọn: A
Câu hỏi 21 :
Cho hình chóp S.ABCD, AB và CD cắt nhau tại I. Phát biểu nào sau đây đúng?
- A Giao tuyến của (SAB) và (SCD) là đường thẳng SI.
- B Giao tuyến của (SAC) và (SCD) là đường thẳng SI.
- C Giao tuyến của (SAB) và (SCD) là đường thẳng SK với K là giao điểm của SD và BC.
- D Giao tuyến của (SOC) và (SAD) là đường thẳng SM với M là giao điểm của AC và SD.
Đáp án: A
Phương pháp giải:
Muốn tìm giao tuyến của hai mặt phẳng cắt nhau ta xác định 2 điểm phân biệt nằm trên cả hai mặt phẳng đó, đường thẳng đi qua 2 điểm này chính là giao tuyến của hai mặt phẳng.
Lời giải chi tiết:
Ta có: \(I = AB \cap CD \Rightarrow \left\{ \begin{array}{l}I \in AB \subset \left( {SAB} \right)\\I \in CD \subset \left( {SCD} \right)\end{array} \right. \Rightarrow I \in \left( {SAB} \right) \cap \left( {SCD} \right)\)
Mà \(S \in \left( {SAB} \right) \cap \left( {SCD} \right) \Rightarrow \left( {SAB} \right) \cap \left( {SCD} \right) = SI\).
Chọn: A
Câu hỏi 22 :
Trong mặt phẳng \(\left( \alpha \right)\), cho bốn điểm \(A,\,B,\,C,\,D\)trong đó không có ba điểm nào thẳng hàng. Điểm \(S \notin \left( \alpha \right)\). Có mấy mặt phẳng tạo bởi \(S\) và hai trong bốn điểm nói trên?
- A 6.
- B 4.
- C 5.
- D 8.
Đáp án: A
Lời giải chi tiết:
Từ 4 điểm \(A,\,B,\,C,\,D\) ghép được 6 cặp điểm \( \Rightarrow \) Có tất cả 6 mặt phẳng tạo bởi \(S\) và hai trong bốn điểm \(A,\,B,\,C,\,D\)
Chọn: A
Câu hỏi 23 :
Cho bốn điểm A, B, C, D không cùng nằm trong một mặt phẳng. Trên AB, AD lần lượt lấy các điểm M, N sao cho MN cắt BD tại I. Điểm I không thuộc mặt phẳng nào sau đây:
- A (ABD).
- B (CMN).
- C (BCD).
- D (ACD).
Đáp án: D
Phương pháp giải:
\(I \in d \subset \left( P \right) \Rightarrow I \in \left( P \right)\)
Lời giải chi tiết:
\(MN \cap BD = I \Rightarrow I \in BD \Rightarrow I \in \left( {ABD} \right) \Rightarrow A\) sai.
\(MN \cap BD = I \Rightarrow I \in MN \Rightarrow I \in \left( {CMN} \right) \Rightarrow B\) sai.
\(MN \cap BD = I \Rightarrow I \in BD \Rightarrow I \in \left( {BCD} \right) \Rightarrow C\) sai.
Chọn đáp án D.
Câu hỏi 24 :
Thiết diện của hình chóp tứ giác (cắt bởi một mặt phẳng) không thể là hình nào dưới đây ?
- A Lục giác
- B Ngũ giác
- C Tam giác
- D Tứ giác
Đáp án: A
Phương pháp giải:
Các đoạn giao tuyến giữa mặt phẳng và hình chóp khi nối tiếp nhau sẽ tạo thành một đa giác phẳng, người ta gọi đó là thiết diện (hay mặt cắt) của mặt phẳng với hình chóp đó.
Lời giải chi tiết:
Chóp tứ giác có 5 mặt nên thiết diện tối đa chỉ có thể là ngũ giác, không thể là lục giác.
Chọn A.
Câu hỏi 25 :
Cho tứ diện ABCD. Gọi M là trung điểm AB, điểm N thuộc đoạn AD sao cho NA=2ND. Giao điểm của MN với mặt phẳng (BCD) là .
- A Điểm I với I là giao điểm của MN với AC.
- B Điểm I với I là giao điểm của MN với CD.
- C Điểm I với I là giao điểm của MN với BD.
- D Điểm I với I là giao điểm của MN với BC.
Đáp án: C
Phương pháp giải:
Xác định giao điểm của MN với 1 đường thẳng nằm trong mặt phẳng (BCD).
Lời giải chi tiết:
Gọi \(I = MN \cap BD \Rightarrow I = MN \cap \left( {BCD} \right)\).
Chọn C.
Câu hỏi 26 :
Tính chất nào sau đây không phải là tính chất của hình lăng trụ đứng?
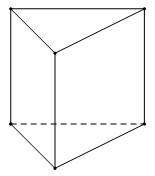
- A Các mặt bên của hình lăng trụ đứng vuông góc với nhau.
- B Các mặt bên của hình lăng trụ đứng là những hình chữ nhật.
- C Các cạnh bên của hình lăng trụ đứng bằng nhau và song song với nhau.
- D Hai đáy của hình lăng trụ đứng có các cạnh tương ứng song song và bằng nhau.
Đáp án: A
Phương pháp giải:
Hình lăng trụ đứng là lăng trụ có cạnh bên vuông góc với đáy.
Lời giải chi tiết:
Các cạnh bên của lăng trụ đứng cùng vuông góc với đáy nên chúng song song với nhau, do đó đáp án A sai.
Chọn A.
Câu hỏi 27 :
Cho \(\left\{ \begin{array}{l}a{\rm{ //}}\left( \alpha \right)\\a \subset \left( \beta \right)\\d = \left( \alpha \right) \cap \left( \beta \right)\end{array} \right.\). Khẳng định nào sau đây đúng ?
- A \(a\) song song với \(d\).
- B \(a\) cắt \(d\).
- C \(a\) trùng \(d\).
- D \(a\) và \(d\) chéo nhau.
Đáp án: A
Lời giải chi tiết:
\(\left\{ \begin{array}{l}a{\rm{ //}}\left( \alpha \right)\\a \subset \left( \beta \right)\\d = \left( \alpha \right) \cap \left( \beta \right)\end{array} \right. \Rightarrow a//d\)
Chọn A.
Câu hỏi 28 :
Cho ba mặt phẳng phân biệt \(\left( \alpha \right),\left( \beta \right),\left( \gamma \right)\)có\(\left( \alpha \right) \cap \left( \beta \right) = {d_1};\left( \beta \right) \cap \left( \gamma \right) = {d_2};\left( \alpha \right) \cap \left( \gamma \right) = {d_3}.\)Khi đó ba đường thẳng \({d_1},{d_2},{d_3}:\)
- A Đôi một song song.
- B Đồng quy.
- C Đôi một cắt nhau.
- D Đôi một song song hoặc đồng quy.
Đáp án: D
Phương pháp giải:
Ba mặt phẳng phân biệt đôi một cắt nhau thì các giao tuyến của chúng hoặc song song hoặc đồng quy.
Lời giải chi tiết:
\(\left. \begin{array}{l}\left( \alpha \right) \cap \left( \beta \right) = {d_1}\\\left( \beta \right) \cap \left( \gamma \right) = {d_2}\\\left( \gamma \right) \cap \left( \alpha \right) = {d_3}\end{array} \right\} \Rightarrow \left[ \begin{array}{l}{d_1}\parallel {d_2}\parallel {d_3}\\{d_1},\,\,{d_2},\,\,{d_3}\,\,dong\,\,quy\end{array} \right.\)
Chọn D.
Câu hỏi 29 :
Cho đường thẳng a và mặt phẳng (P) không chứa a. Hai đường thẳng b và c cùng nằm trong mặt phẳng (P) và cùng cắt đường thẳng a. Khả năng nào sau đây không thể xảy ra?
- A Hai đường thẳng b và c trùng nhau
- B Hai đường thẳng b và c cắt nhau tại một điểm thuộc (P)
- C Hai đường thẳng b và c cắt nhau tại một điểm thuộc đường thẳng a
- D Hai đường thẳng b và c song song với nhau
Đáp án: D
Phương pháp giải:
Giao điểm của đường thẳng a và mp(P) là giao điểm của đường thẳng a và một đường thẳng khác nằm trong (P).
Lời giải chi tiết:
Giả sử đường thẳng b cắt đường thẳng a tại M thì M là giao điểm của a và (P)
Tương tự đường thẳng c cắt a tại M’ và M’ cũng là giao điểm của a và (P)
⇒ M ≡ M’
Vậy hai đường thẳng b và c cắt nhau
Chọn đáp án D
Câu hỏi 30 :
Cho tứ diện ABCD. Trên cạnh AB, AC lấy các điểm M, N sao cho MN cắt BC tại E và O là điểm bất kì trong tam giác BCD. Kết luận nào sau đây đúng ?
(I) Giao điểm của (OMN) và BC là điểm E.
(II) Giao điểm của (OMN) và BD là giao điểm của BD và OE.
(III) Giao điểm của (OMN) và CD là giao điểm của CD và ON.
- A Cả ba đều đúng
- B Chỉ có (I) đúng.
- C Chỉ có (I) và (II) đúng
- D Chỉ có (I) và (III) đúng.
Đáp án: C
Phương pháp giải:
Suy luận từng đáp án dựa vào giao điểm của đường thẳng và mặt phẳng.
Lời giải chi tiết:
\(E \in BC,E \in MN \subset \left( {OMN} \right) \Rightarrow E = BC \cap \left( {OMN} \right) \Rightarrow \) (I) đúng.
Trong (BCD) gọi \(F = OE \cap BD \Rightarrow F = BD \cap \left( {OMN} \right) \Rightarrow \) (II) đúng.
Trong (BCD) gọi \(G = OE \cap CD \Rightarrow G = \left( {OMN} \right) \cap CD \Rightarrow \) (III) sai.
Chọn đáp án C.
Câu hỏi 31 :
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N và P lần lượt là trung điểm của các cạnh SA, BC và CD. Hỏi thiết diện của hình chóp cắt bởi mặt phẳng (MNP) là hình gì?
- A Hình ngũ giác.
- B Hình tam giác.
- C Hình tứ giác.
- D Hình bình hành.
Đáp án: A
Lời giải chi tiết:
Trong mặt phẳng (ABCD): gọi I và J lầm lượt là giao điểm của PN với AB, AD.
Trong mặt phẳng (SAD): gọi K là giao điểm của MJ và SD.
Trong mặt phẳng (SAB): gọi H là giao điểm của MJ và SB.
Vậy, thiết diện của hình chóp cắt bởi mặt phẳng (MNP) là ngũ giác MHNPK.
Chọn: A.
Câu hỏi 32 :
Cho hình chóp SABCD có đáy là hình bình hành. Gọi M là trung điểm của SD, N là trọng tâm tam giác SAB. Đường thẳng MN cắt mặt phẳng (SBC) tại điểm I. Tỉnh tỉ số \(\frac{IN}{IM}.\)
- A \(\frac{3}{4}\)
- B \(\frac{1}{3}\)
- C \(\frac{1}{2}\)
- D \(\frac{2}{3}\)
Đáp án: D
Phương pháp giải:
+) Tìm giao điểm của I của MN với mặt phẳng (SBC).
+) Sau đó áp dụng các tính chất để tìm tỉ lệ đề bài yêu cầu.
Lời giải chi tiết:
Gọi K là trung điểm của AB.
Theo tính chất trọng tâm tam giác SAB ta có:
\(\frac{SN}{SK}=\frac{2}{3}.\)
Trong mặt phẳng (SDK), kéo dài DK cắt BC tại điểm E.
Xét tam giác \(\Delta SDE\) ta có:
EM và SK là hai đường trung tuyến của tam giác.
Lại có: \(\frac{SN}{SK}=\frac{2}{3}\)
\(\Rightarrow N\) là trọng tâm \(\Delta SDE\Rightarrow M,\ N,\ E\) thẳng hàng
\(\Rightarrow I\equiv E.\)
\(\Rightarrow \frac{IN}{IM}=\frac{2}{3}\) (tính chất trọng tâm tam giác).
Chọn D.
Câu hỏi 33 :
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm O, M nằm giữa BO. Mặt phẳng \(\left( \alpha \right)\) qua M song song với SB và AC. Thiết diện của mặt phẳng \(\left( \alpha \right)\) với hình chóp là:
- A Ngũ giác
- B Tam giác
- C Hình bình hành
- D Hình thang không phải hình bình hành
Đáp án: A
Phương pháp giải:
Áp dụng cách tìm thiết diện của mặt phẳng với hình chóp
Lời giải chi tiết:
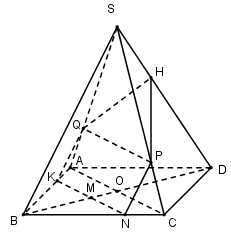
Qua M kẻ \(KN\parallel AC\left( {K \in AB,N \in BC} \right),HM\parallel SB\left( {H \in SD} \right) \Rightarrow K,N \in \left( \alpha \right)\)
Qua N kẻ \(NP\parallel SB\parallel HM\,\,\left( {P \in SC} \right) \Rightarrow P \in \left( \alpha \right)\)
Qua P kẻ \(PQ\parallel AC\,\,\left( {Q \in SA} \right) \Rightarrow Q \in \left( \alpha \right) \Rightarrow KNPHQ\) là thiết diện của bài toán
Chọn A.
Câu hỏi 34 :
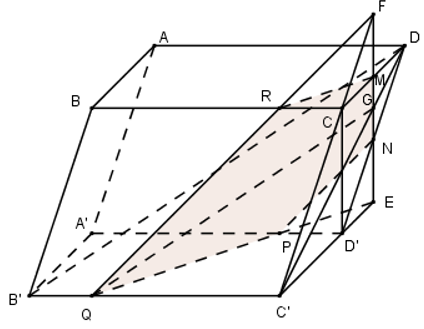
Cho hình hộp ABCD.A’B’C’D’, gọi M là trung điểm của CD, (P) là mặt phẳng đi qua M và song song với B’D và CD’. Thiết diện của hình hộp cắt bởi (P) là hình gì?
- A Ngũ giác
- B Tứ giác
- C Tam giác
- D Lục giác
Đáp án: A
Phương pháp giải:
Sử dụng tính chất \(\left\{ \begin{align} & \left( P \right)\supset a \\ & \left( Q \right)\supset b \\ & a//b \\ \end{align} \right.\Rightarrow \left( P \right)\cap \left( Q \right)=d//a//b\)
Lời giải chi tiết:
Trong (CDD’C’) qua M kẻ MN // C’D \(\left( N\in \text{DD}' \right)\)
Gọi \(G=MN\cap DC'\Leftrightarrow G\in \left( B'C'D \right)\)
Trong (B’C’D) qua G kẻ GQ // B’D \(\left( Q\in B'C' \right)\)
Kéo dài MN, gọi \(E=MN\cap C'D'\)
\(\Rightarrow E\in \left( A'B'C'D' \right),F=MN\cap CC'\Rightarrow F\in \left( BCC'B' \right)\)
Trong (A’B’C’D’) gọi \(P=EQ\cap A'D'\)
Trong (BCC’B’) gọi \(R=QF\cap BC\)
Vậy thiết diện cần tìm là ngũ giác MNPQR.
Chọn A.
Câu hỏi 35 :
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Điểm M thỏa mãn \(\overrightarrow{MA}=3\overrightarrow{MB}\). Mặt phẳng (P) qua M và song song với hai đường thẳng SC, BD. Mệnh đề nào sau đây đúng?
- A (P) không cắt hình chóp.
- B (P) cắt hình chóp theo thiết diện là một tứ giác.
- C (P) cắt hình chóp theo thiết diện là một tam giác.
- D (P) cắt hình chóp theo thiết diện là một ngũ giác.
Đáp án: D
Phương pháp giải:
Qua M dựng các đường thẳng song song với BD và SC.
Lời giải chi tiết:
Lấy điểm M thỏa mãn \(\overrightarrow{MA}=3\overrightarrow{MB}\) như hình vẽ.
Trong (ABCD) qua M kẻ đường thẳng song song với BD cắt BC tại E và cắt CD tại F.
Trong (SCD) qua F kẻ FP // SC \(\left( P\in SD \right)\)
Trong (SBD) qua M kẻ MN // BD \(\left( N\in SB \right)\)
Trong (SAB) kéo dài MN cắt SA tại H.
Vậy thiết diện của chóp khi cắt bởi mặt phẳng (P) là ngũ giác EFPHN.
Chọn D.
Câu hỏi 36 :
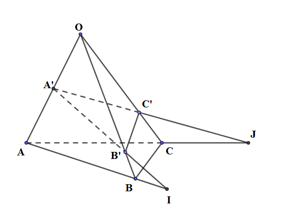
Cho hình chóp \(O.ABC\), \(A'\)là trung điểm của OA, B’, C’ lần lượt thuộc các cạnh OB, OC và không phải là trung điểm của các cạnh này. Phát biểu nào sau đây sai?
- A Mặt phẳng (ABC) và mặt phẳng (A’B’C’) không có điểm chung.
- B Đường thẳng OA và B’C’ không cắt nhau.
- C Đường thẳng AC và A’C’ cắt nhau tại một điểm thuộc mặt phẳng (ABC).
- D Đường thẳng AB và A’B’ cắt nhau tại một điểm thuộc mặt phẳng (ABC).
Đáp án: A
Phương pháp giải:
Xác định giao tuyến của hai mặt phẳng (ABC) và (A’B’C’).
Lời giải chi tiết:
Gọi I, J lần lượt là giao điểm của A’C’ và AC; A’B’ và AB
Khi đó \(\left( {ABC} \right) \cap \left( {A'B'C'} \right) = IJ\)
\( \Rightarrow \) Mặt phẳng (ABC) và mặt phẳng (A’B’C’) không có điểm chung: là sai.
Chọn: A
Câu hỏi 37 :
Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AD. Gọi M là trung điểm của CD. Giao tuyến của hai mặt phẳng (SMB) và (SAC) là đường thẳng
- A SI với I là giao điểm của AC và BM.
- B SP với P là giao điểm của AB và CD.
- C SJ với J là giao điểm của AM và BD.
- D SO với O là giao điểm của AC và BD.
Đáp án: A
Phương pháp giải:
Xác định các điểm chung.
Lời giải chi tiết:
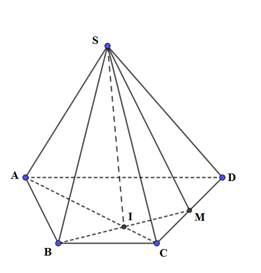
Giao tuyến của hai mặt phẳng (SMB) và (SAC) là đường thẳng SI với I là giao điểm của AC và BM.
Chọn: A
Câu hỏi 38 :
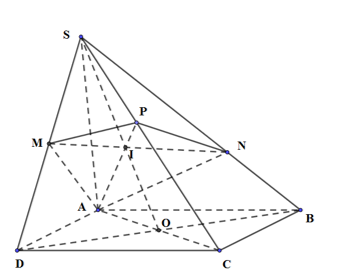
Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành. Gọi M là trung điểm của SD, điểm N nằm trên cạnh SB sao cho\(SN = 2NB\) và O là giao điểm của AC và BD. Khẳng định nào sau đây là sai?
- A Đường thẳng MN cắt mặt phẳng (ABCD).
- B Thiết diện của hình chóp S.ABCD với mặt phẳng (AMN) là một hình thang.
- C Hai đường thẳng MN và SO cắt nhau.
- D Hai đường thẳng MN và SC chéo nhau.
Đáp án: B
Lời giải chi tiết:
+) Ta có: \(\frac{{SM}}{{SD}} = \frac{1}{2},\,\,\frac{{SN}}{{SB}} = \frac{2}{3} \Rightarrow MN\)không song song \(BD\)
Mà \(\left\{ \begin{array}{l}MN \subset \left( {SBD} \right)\\\left( {SBD} \right) \cap \left( {ABCD} \right) = BD\end{array} \right.\)
\( \Rightarrow \) MN không song song với (ABCD)
\( \Rightarrow \) Đường thẳng MN cắt mặt phẳng (ABCD) (do \(MN \not\subset \left( {ABCD} \right)\))
+) Gọi \(I = MN \cap SO,\,\,P = AI \cap SC\)
\( \Rightarrow \) Thiết diện của hình chóp S.ABCD với mặt phẳng (AMN) là tứ giác \(AMPN\), đây không phải là hình thang.
+) Hai đường thẳng MN và SO cắt nhau và Hai đường thẳng MN và SC chéo nhau là hai khẳng định đúng.
Chọn: B
Câu hỏi 39 :
Cho tứ diện ABCD. Gọi E, F lần lượt là trung điểm của AB, CD và G là trọng tâm tam giác BCD. Giao điểm của đường thẳng EG và mặt phẳng (ACD) là:
- A Giao điểm của đường thẳng EG và AC.
- B Điểm F.
- C Giao điểm của đường thẳng EG và AF.
- D Giao điểm của đường thẳng EG và CD.
Đáp án: C
Phương pháp giải:
* Cách xác định giao điểm của đường thẳng a và mặt phẳng (a):
- Chọn mp phụ (b) chứa đường thẳng a sao cho giao tuyến của mp (a) và mp (b) dễ xác định
- Tìm giao tuyến b của mp (a) và mp (b)
- b cắt a tại I
Khi đó I là giao điểm của a và mặt phẳng (a).
Lời giải chi tiết:
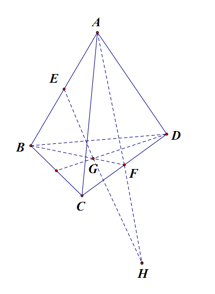
Ta có: \(\left\{ \begin{array}{l}EG \subset \left( {ABF} \right)\\AF = \left( {ABF} \right) \cap \left( {ACD} \right)\end{array} \right.\) \( \Rightarrow \) Giao điểm của đường thẳng EG và mặt phẳng (ACD) là giao điểm của đường thẳng EG và AF.
Chọn: C
Câu hỏi 40 :
Cho hình chóp S.ABCD. Gọi C’ là điểm nằm trên cạnh SC sao cho \(SC' = \frac{2}{3}SC\). Thiết diện của hình chóp với mặt phẳng (ABC’) là một đa giác có m cạnh. Tìm m.
- A \(m = 6\).
- B \(m = 4\).
- C \(m = 5\).
- D \(m = 3\).
Đáp án: B
Lời giải chi tiết:
Gọi \(O = AC \cap BD\), \(I = SO \cap AC'\), \(D' = SD \cap IB\)
Thiết diện của hình chóp với mặt phẳng (ABC’) là tứ giác \(ABC'D'\)
\( \Rightarrow m = 4\).
Chọn: B
Câu hỏi 41 :
Cho hình chóp\(S.ABCD\) có đáy\(ABCD\) là hình bình hành. Gọi M, N lần lượt là trung điểm của AD và BC. Giao tuyến của hai mặt phẳng (SMN) và (SAC) là
- A SG (G là trung điểm AB).
- B SD.
- C SF (F là trung điểm CD).
- D SO (O là tâm hình bình hành ABCD).
Đáp án: D
Phương pháp giải:
Xác định 2 điểm chung.
Lời giải chi tiết:
Gọi O là giao điểm của MN và AC \( \Rightarrow \left( {SAC} \right) \cap \left( {SMN} \right) = SO\)
Ta có: AMCN là hình bình hành (do AM song song và bằng NC)
\( \Rightarrow \) O là trung điểm của AC và MN
Mà ABCD là hình bình hành \( \Rightarrow \) O là trung điểm của AC và BD
\( \Rightarrow O = BD \cap AC\)
Vậy giao tuyến của hai mặt phẳng (SMN) và (SAC) là SO (O là tâm hình bình hành ABCD).
Chọn: D
Câu hỏi 42 :
Cho hình chóp tứ giác S.ACBD, gọi M, N, P, Q, R, T lần lượt là trung điểm của AC, BD, BC, CD, SA, SD. Bốn điểm nào sau đây đồng phẳng?
- A M, P, R, T.
- B M, Q, R, T.
- C M, N, R, T.
- D P, Q, R, T.
Đáp án: B
Phương pháp giải:
Nếu \(a//a'\) thì \(a\) và \(a'\) đồng phẳng.
Lời giải chi tiết:
Ta có: \(RT//AD\) (do \(RT\) là đường trung bình của tam giác \(SAD\))
\(MQ//AD\) (do \(RT\) là đường trung bình của tam giác \(ACD\))
\( \Rightarrow RT//MQ \Rightarrow \) M, Q, R, T đồng phẳng.
Chọn: B
Câu hỏi 43 :
Chọn mệnh đề đúng trong các mệnh đề sau:
- A Có duy nhất một mặt phẳng đi qua 4 điểm không thẳng hàng.
- B Có duy nhất một mặt phẳng đi qua một đường thẳng và một điểm.
- C Có duy nhất một mặt phẳng đi qua ba điểm.
- D Có duy nhất một mặt phẳng đi qua hai đường thẳng song song cho trước.
Đáp án: D
Phương pháp giải:
Sử dụng các cách xác định mặt phẳng.
Lời giải chi tiết:
Có 3 cách xác định mặt phẳng:
+) Có duy nhất một mặt phẳng đi qua ba điểm không thẳng hàng.
+) Có duy nhất một mặt phẳng đi qua một đường thẳng và một điểm không thuộc đường thẳng.
+) Có duy nhất một mặt phẳng đi qua hai đường thẳng song song cho trước.
Chọn D.
Câu hỏi 44 :
Cho hình chóp \(S.ABCD\) có \(O\) là giao điểm của \(AC\) và \(BD\). Giao tuyến của hai mặt phẳng \(\left( {SAO} \right)\) và \(\left( {SBD} \right)\) là đường thẳng:
- A \(SA\)
- B \(SB\)
- C \(SC\)
- D \(SO\)
Đáp án: D
Phương pháp giải:
Xác định hai điểm chung của hai mặt phẳng.
Lời giải chi tiết:
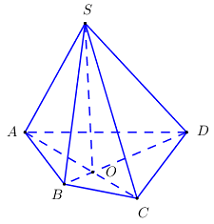
Dễ thấy \(\left( {SAO} \right)\) và \(\) có 1 điểm chung là \(S\).
Ta có \(O = AC \cap BD \Rightarrow \left\{ \begin{array}{l}O \in AO \subset \left( {SAO} \right)\\O \in BD \subset \left( {SBD} \right)\end{array} \right. \Rightarrow O \in \left( {SAO} \right) \cap \left( {SBD} \right)\).
Vậy \(\left( {SAO} \right) \cap \left( {SBD} \right) = SO\) với \(O = AC \cap BD\).
Chọn D.
Câu hỏi 45 :
Trong mặt phẳng \(\left( P \right)\) cho tứ giác lồi \(ABCD\), \(S\) là điểm nằm ngoài mặt phẳng \(\left( P \right)\), \(O\) là giao điểm của \(AC\) và \(BD\), \(M\) là trung điểm của \(SC\). Hai đường thẳng nào sau đây cắt nhau ?
- A \(SO\) và \(AM\)
- B \(AM\) và \(SB\)
- C \(BM\) và \(SD\)
- D \(DM\) và \(SB\)
Đáp án: A
Phương pháp giải:
Hai đường thẳng trong không gian cắt nhau khi và chỉ khi chúng đồng phẳng và không song song.
Lời giải chi tiết:
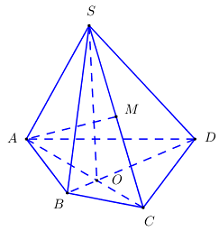
Ta có \(M\) là trung điểm của \(SC \Rightarrow M \in SC \subset \left( {SAC} \right) \Rightarrow M \in \left( {SAC} \right)\).
\( \Rightarrow AM \subset \left( {SAC} \right)\).
\(O = AC \cap BD \Rightarrow O \in AC \subset \left( {SAC} \right) \Rightarrow O \in \left( {SAC} \right)\).
\( \Rightarrow SO \subset \left( {SAC} \right)\).
Do đó \(AM,\,\,SO\) đồng phẳng và không song song, vậy chúng cắt nhau.
Chọn A
Câu hỏi 46 :
Hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cắt nhau theo giao tuyến \(d\). Trong \(\left( P \right)\) cho đường thẳng \(a\), trong \(\left( Q \right)\) cho đường thẳng \(b\). Giả sử \(a \cap b = M,\,\,a \cap d = N,\,\,b \cap d = K\). Phát biểu nào sau đây là đúng?
- A Ba điểm \(M,\,\,N,\,\,K\) thẳng hàng.
- B Ba điểm \(M,\,\,N,\,\,K\) trùng nhau.
- C Ba điểm \(M,\,\,N,\,\,K\) lập thành tam giác cân.
- D Ba điểm \(M,\,\,N,\,\,K\) lập thành tam giác vuông.
Đáp án: B
Lời giải chi tiết:
Ta có \(\left\{ \begin{array}{l}a \cap b = M\\b \subset \left( Q \right)\end{array} \right. \Rightarrow a \cap \left( Q \right) = M\).
\(\left\{ \begin{array}{l}a \cap d = N\\d = \left( P \right) \cap \left( Q \right) \Rightarrow d \subset \left( Q \right)\end{array} \right. \Rightarrow a \cap \left( Q \right) = N\)
\( \Rightarrow M \equiv N\).
Chứng minh tương tự ta có \(P \equiv N\).
Vậy ba điểm \(M,\,\,N,\,\,K\) trùng nhau.
Chọn B
Câu hỏi 47 :
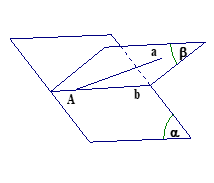
Cho tứ diện đều \(ABCD\) cạnh \(a\). Tính góc giữa hai đường thẳng \(IC\) và \(AC\), với \(I\) là trung điểm của \(AB\).
- A \({150^0}\)
- B \({30^0}\)
- C \({170^0}\)
- D \({10^0}\)
Đáp án: B
Phương pháp giải:
Sử dụng các tính chất của tam giác đều.
Lời giải chi tiết:
Tam giác \(ABC\) đều \( \Rightarrow \) Trung tuyến \(IC\) đồng thời là phân giác.
\( \Rightarrow \angle \left( {IC;AC} \right) = \angle ACI = \dfrac{1}{2}{.60^0} = {30^0}\).
Chọn B.
Câu hỏi 48 :
Cho tứ diện \(ABCD.\) Gọi \(G\) là trọng tâm tam giác \(\Delta ABC\). Gọi \(I\) là hình chiếu song song của \(G\)lên mặt phẳng \(\left( {BCD} \right)\) theo phương chiếu \(AD.\) Chọn khẳng định đúng.
- A \(I\) là điểm bất kì trong tam giác \(\Delta BCD.\)
- B \(I\) là trực tâm tam giác \(\Delta BCD.\)
- C \(I\) là trọng tâm tam giác \(\Delta BCD.\)
- D \(I\) là thỏa mãn \(IG \bot \left( {BCD} \right).\)
Đáp án: C
Phương pháp giải:
+) \(I\) là hình chiếu của \(G\) lên mặt phẳng \(\left( {BCD} \right)\) theo phương chiếu \(AD\) \( \Rightarrow GI//AD\).
+) Áp dụng định lí Ta-lét.
Lời giải chi tiết:
Gọi \(M\) là trung điểm của \(BC\).
Trong \(\left( {AMD} \right)\) kẻ \(GI//AD,\,\,I \in MD \Rightarrow I \in \left( {BCD} \right)\)
Khi đó \(I\) là hình chiếu của \(G\) lên mặt phẳng \(\left( {BCD} \right)\) theo phương chiếu \(AD\).
Áp dụng định lí Ta-lét ta có: \(\dfrac{{DI}}{{DM}} = \dfrac{{AG}}{{AM}} = \dfrac{2}{3}\), lại có \(DM\) là trung tuyến của \(\Delta BCD \Rightarrow I\) là trọng tâm tam giác \(BCD\).
Chọn C.
Câu hỏi 49 :
Cho bốn điểm \(A,\,\,B,\,\,C,\,\,D\) không cùng nằm trên một mặt phẳng. Trên \(AB,\,\,AD\) lần lượt lấy các điểm \(M\) và \(N\) sao cho \(MN\) cắt \(BD\) tại \(I\). Điểm \(I\) không thuộc mặt phẳng nào sau đây?
- A \(\left( {BCD} \right)\)
- B \(\left( {ABD} \right)\)
- C \(\left( {CMN} \right)\)
- D \(\left( {ACD} \right)\)
Đáp án: D
Phương pháp giải:
\(\left\{ \begin{array}{l}I \in d\\d \subset \left( P \right)\end{array} \right. \Rightarrow I \in \left( P \right)\).
Lời giải chi tiết:
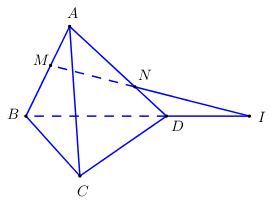
Ta có \(I = MN \cap BD \Rightarrow \left\{ \begin{array}{l}I \in MN \subset \left( {CMN} \right)\\I \in BD \subset \left( {BCD} \right)\\I \in BD \subset \left( {ABD} \right)\end{array} \right.\).
Do đó điểm \(I\) thuộc các mặt phẳng \(\left( {BCD} \right),\,\,\,\left( {ABD} \right),\,\,\left( {CMN} \right)\).
Chọn D
Câu hỏi 50 :
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang \(\left( {AD\parallel BC} \right)\). Gọi \(M\) là trung điểm của \(CD\). Giao tuyến của hai mặt phẳng \(\left( {MSB} \right)\) và \(\left( {SAC} \right)\) là:
- A \(SI\) với \(I = AC \cap BM\)
- B \(SJ\) với \(J = AM \cap BD\)
- C \(SO\) với \(O = AC \cap BD\)
- D
\(SP\) với \(P = AB \cap CD\)
Đáp án: A
Phương pháp giải:
Xác định hai điểm chung của hai mặt phẳng.
Lời giải chi tiết:
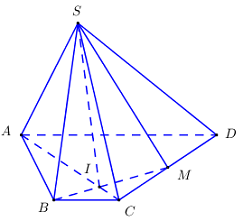
Trong \(\left( {ABCD} \right)\) gọi \(I = AC \cap BM\).
Ta có \(\left\{ \begin{array}{l}I \in AC \subset \left( {SAC} \right)\\I \in BM \subset \left( {MSB} \right)\end{array} \right. \Rightarrow I\) là điểm chung của \(\left( {SAC} \right)\) và \(\left( {MSB} \right)\).
Dễ thấy \(\left( {SAC} \right)\) và \(\left( {MSB} \right)\) có điểm chung thứ hai là \(S\).
Vậy \(SI\) với \(I = AC \cap BM\).
Chọn A
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
