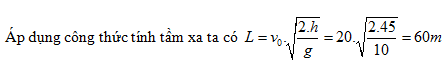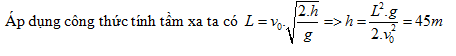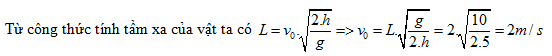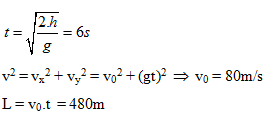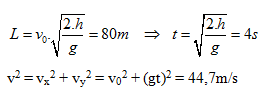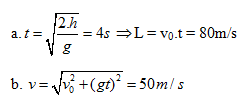50 bài tập Bài toán về chuyển động ném ngang mức độ vận dụng

Câu hỏi 1 :

Một vật được ném theo phương ngang với vận tốc 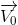$\overrightarrow {{V_0}}$ từ độ cao h so với mặt đất. Chọn hệ trục toạ độ Oxy sao cho gốc O trùng với vị trí ném, Ox theo chiều 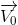$\overrightarrow {{V_0}}$ , Oy hướng thẳng đứng xuống dưới, gốc thời gian là lúc ném. Phương trình quỹ đạo của vật:

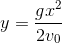
A $y = {{g{x^2}} \over {2{v_0}}}$
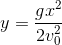
B $y = {{g{x^2}} \over {2v_0^2}}$
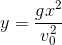
C $y = {{g{x^2}} \over {v_0^2}}$
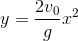
D $y = {{2{v_0}} \over g}{x^2}$

Đáp án: B

Lời giải chi tiết:

Đáp án B

Phương trình quỹ đạo của vật là 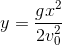$y = {{g{x^2}} \over {2v_0^2}}$

Đáp án - Lời giải

Câu hỏi 2 :

Một vật được ném theo phương ngang với vận tốc 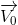$\overrightarrow {{V_0}}$ từ độ cao h so với mặt đất. Chọn hệ trục toạ độ Oxy sao cho gốc O trùng với vị trí ném, Ox theo chiều 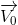$\overrightarrow {{V_0}}$ , Oy hướng thẳng đứng xuống dưới, gốc thời gian là lúc ném. Tầm xa L tính theo phương ngang xác định bằng biểu thức:

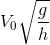
A ${V_0}\sqrt {{g \over h}}$
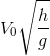
B ${V_0}\sqrt {{h \over g}}$
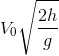
C ${V_0}\sqrt {{{2h} \over g}}$
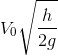
D ${V_0}\sqrt {{h \over {2g}}}$

Đáp án: C

Lời giải chi tiết:

Đáp án C

Tầm xa L tính theo phương ngang xác định bằng biểu thức 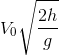${V_0}\sqrt {{{2h} \over g}}$

Đáp án - Lời giải

Câu hỏi 3 :

Một người chạy bộ với vận tốc có độ lớn không đổi v xuyên qua một rừng thông. Khi người đó vừa chạy tới bên dưới một gốc thông thì có một trái thông từ cây đó rơi thẳng xuống từ độ cao h (bỏ qua ma sát). Hỏi khi trái thông vừa chạm xuống đất người chạy bộ cách trái thông một khoảng là bao nhiêu?

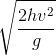
A $\sqrt{\frac{2hv^{2}}{g}}$
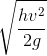
B $\sqrt{\frac{hv^{2}}{2g}}$
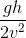
C $\frac{gh}{2v^{2}}$
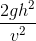
D $\frac{2gh^{2}}{v^{2}}$

Đáp án: A

Lời giải chi tiết:

Đáp án A

Đáp án - Lời giải

Câu hỏi 4 :

Một quả bóng được ném theophương ngang với vận tốc đầu có độ lớn là v_o = 20m/s từ độ cao 45m và rơi xuống đất sau 3s. Hỏi tầm bay xa (theo phương ngang) của quả bóng bằng bao nhiêu ? Lấy g = 10m/s² và bỏ qua sức cản của không khí.

A 30m
B 45m
C 60m
D 90m

Đáp án: C

Lời giải chi tiết:

Áp dụng công thức tính tầm xa ta có $L = v_{0}.t = 20.3 = 60 m$

Đáp án - Lời giải

Câu hỏi 5 :

Một hòn bi lăn dọc theo một cạnh của một mặt bàn hình chữ nhật nằm ngang cao h = 1,25m. Khi ra khỏi mép bàn, nó rơi xuống nền nhà tại điểm cách mép bàn L = 1,50m (theo phương ngang). Lấy g = 10m/s². Thời gian rơi của bi là:

A 0,25s
B 0,35s
C 0,5s
D 0,125s

Đáp án: C

Lời giải chi tiết:

áp dụng công thức tính tầm xa của vật ta có

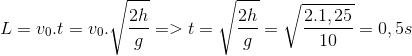
$L= v_{0}.t = v_{0}.\sqrt{\frac{2h}{g}}=>t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2.1,25}{10}}=0,5 s$

Đáp án - Lời giải

Câu hỏi 6 :

Một máy bay đang bay ngang với vận tốc V₁ ở độ cao h so với mặt đất muốn thả bom trúng một đoàn xe tăng đang chuyển động với vận tốc V₂ trong cùng 2 mặt phẳng thẳng đứng với máy bay. Hỏi còn cách xe tăng bao xa thì cắt bom (đó là khoảng cách từ đường thẳng đứng qua máy bay đến xe tăng) khi máy bay và xe tăng chuyển động cùng chiều.

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 7 :

Một quả bóng được ném theo phương ngang với vận tốc đầu có độ lớn là vo = 20m/s từ độ cao 45m và rơi xuống đất sau 3s. Hỏi tầm bay xa (theo phương ngang) của quả bóng bằng bao nhiêu ? Lấy g = 10m/s2 và bỏ qua sức cản của không khí.

A 30m
B 45m
C 60m
D 90m

Đáp án: C

Lời giải chi tiết:

Đáp án C

Đáp án - Lời giải

Câu hỏi 8 :

Một hòn bi lăn dọc theo một cạnh của một mặt bàn hình chữ nhật nằm ngang cao h = 1,25m. Khi ra khỏi mép bàn, nó rơi xuống nền nhà tại điểm cách mép bàn L = 1,50m (theo phương ngang). Lấy g = 10m/s2. Thời gian rơi của bi là :

A 0,25s
B 0,35s
C 0,5s
D 0,125

Đáp án: C

Lời giải chi tiết:

Đáp án C

Đáp án - Lời giải

Câu hỏi 9 :

Một quả bóng được ném theo phương ngang với vận tốc đầu có độ lớn là v_o = 20m/s và rơi xuống đất sau 3s. Hỏi quả bóng được ném từ độ cao nào ? Lấy g = 10m/s² và bỏ qua sức cản của không khí.

A 30m
B 45m
C 60m
D 90m

Đáp án: B

Lời giải chi tiết:

Đáp án B

Đáp án - Lời giải

Câu hỏi 10 :

Một quả bóng được ném theo phương ngang với vận tốc đầu có độ lớn là v_o = 20m/s từ độ cao 45m và rơi xuống đất sau 3s. Hỏi tầm bay xa (theo phương ngang) của quả bóng bằng bao nhiêu ? Lấy g = 10m/s² và bỏ qua sức cản của không khí.

A 30m
B 45m
C 60m
D 90m

Đáp án: C

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 11 :

Một hòn bi lăn dọc theo một cạnh của một mặt bàn hình chữ nhật nằm ngang cao h = 1,25m. Khi ra khỏi mép bàn, nó rơi xuống nền nhà tại điểm cách mép bàn L = 1,50m (theo phương ngang). Lấy g = 10m/s². Thời gian rơi của bi là :

A 0,25s
B 0,35s
C 0,5s
D 0,125s

Đáp án: C

Đáp án - Lời giải

Câu hỏi 12 :

Một quả bóng được ném theo phương ngang với vận tốc đầu có độ lớn là v_o = 20m/s và rơi xuống đất sau 3s. Hỏi quả bóng được ném từ độ cao nào ? Lấy g = 10m/s² và bỏ qua sức cản của không khí.

A 30m
B 45m
C 60m
D 90m

Đáp án: B

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 13 :

Chọn đáp án đúng. Trong chuyển động ném ngang, chuyển động của chất điểm là:

A Chuyển động thẳng đều
B Chuyển động rơi tự do
C Chuyển động thẳng đều theo phương ngang, rơi tự do theo phương thẳng đứng
D Chuyển động thẳng biến đổi đều

Đáp án: C

Phương pháp giải:

Phân tích chuyển động ném ngang thành 2 chuyển động trên Ox và Oy.

Trên Ox: Vật chuyển động thẳng đều với vận tốc: ${v_x} = {v_0}$

Trên Oy: Vật chuyển động rơi tự do.

Lời giải chi tiết:

Trong chuyển động ném ngang, chuyển động của chất điểm là: Chuyển động thẳng đều theo phương ngang, rơi tự do theo phương thẳng đứng.

Chọn C.

Đáp án - Lời giải

Câu hỏi 14 :

Một vật được ném ngang từ độ cao h = 9m. Vận tốc ban đầu có độ lớn là v_o. Tầm xa của vật 18m. Tính v_o. Lấy g = 10m/s².

A 19m/s
B 13,4m/s
C 10m/s
D 3,16m/s

Đáp án: B

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 15 :

Một vật được ném ngang từ độ cao 5m, tầm xa vật đạt được là 2m. Vận tốc ban đầu của vật là: (Lấy g =10 m/s²)

A 10 m/s.
B 2,5 m/s.
C 5 m/s.
D 2 m/s.

Đáp án: D

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 16 :

Một vật được ném theo phương ngang với vận tốc 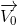$\overrightarrow {{V_0}}$ từ độ cao h so với mặt đất. Chọn hệ trục toạ độ Oxy sao cho gốc O trùng với vị trí ném, Ox theo chiều 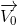$\overrightarrow {{V_0}}$ , Oy hướng thẳng đứng xuống dưới, gốc thời gian là lúc ném. Thời gian chuyển động của vật từ lúc ném đến lúc chạm đất xác định bằng biểu thức:

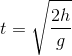
A $t = \sqrt {{{2h} \over g}}$
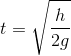
B $t = \sqrt {{{h} \over 2g}}$
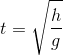
C $t = \sqrt {{{h} \over g}}$
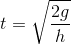
D $t = \sqrt {{{2g} \over h}}$

Đáp án: A

Lời giải chi tiết:

Đáp án A

Thời gian chuyển động của vật từ lúc ném đến lúc chạm đất xác định bằng biểu thức 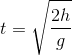$t = \sqrt {{{2h} \over g}}$

Đáp án - Lời giải

Câu hỏi 17 :

Một viên đạn được bắn theo phương ngang ở độ cao 180m phải có vận tốc ban đầu là bao nhiêu để ngay lúc chạm đất có v = 100m/s. Tính tầm ném xa của vật khi chạm đất.

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 18 :

Một máy bay ném bom bay theo phương ngang ở độ cao 2km với v = 504km/h. Hỏi viên phi công phải thả bom từ xa cách mục tiêu ( theo phương ngang) bao nhiêu để bơm rơi trúng mục tiêu?, lấy g = 10m/s².

Lời giải chi tiết:

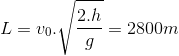
$L = {v_0}.\sqrt {{{2.h} \over g}} = 2800m$

Đáp án - Lời giải

Câu hỏi 19 :

Từ độ cao h = 80m, người ta ném một quả cầu theo phương nằm ngang với v₀ = 20m/s. Xác định vị trí và vận tốc của quả cầu khi chạm đất. Cho rằng sức cản của KK không đáng kể, g = 10m/s²

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 20 :

Một vật được ném thẳng đứng xuống dưới từ vị trí cách mặt đất 30m, v₀ = 5m/s, lấy g = 10m/s². Bỏ qua sức cản của không khí.

a) Thời gian từ lúc ném đến lúc vật chạm đất.

b) Vận tốc của vật lúc chạm đất.

Lời giải chi tiết:

a) Chọn trục toạ độ thẳng đứng, gốc toạ tại điểm ném, chiều dương là chiều chuyển động của vật.

Phương trình chuyển động của vật là: $y = {v_0}t + {1 \over 2}g{t^2} = 5t + 5{t^2}$

Khi chạm đất ta có:

$y = 30m \Leftrightarrow 5t + 5{t^2} = 30 \Rightarrow t = 2s$

b) Vận tốc của vật lúc chạm đất là:

$v = {v_0} + at = 5 + 10.2 = 25m/s$

Đáp án - Lời giải

Câu hỏi 21 :

Từ sân thượng cao 20m một người đã ném một hòn sỏi theo phương ngang với v₀ = 4m/s, g = 10m/s².

a/ Viết pt chuyển động của hòn sỏi theo trục Ox, Oy.

b/ Viết pt quỹ đạo của hòn sỏi.

c/ Hòn sỏi đạt tầm xa bằng bao nhiêu? Vận tốc của nó khi vừa chạm đất.

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 22 :

Từ một đỉnh tháp cao 80m, một vật nhỏ được ném theo phương ngang với v₀ = 20m/s, g = 10m/s².

a/ Vật chạm đất cách chân tháp bao xa.

b/ Tính tốc độ chạm đất của vật.

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 23 :

Một vật được ném thẳng đứng từ mặt đất lên cao với v = 57,6km/h, g = 10m/s². Bỏ qua ma sát.

a/ Viết pt gia tốc, vận tốc và pt toạ độ theo thời gian.

b/ Xác định độ cao cực đại của vật.

c/ Xác định khoảng thời gian từ khi ném đến khi vật rơi trở lại mặt đất.

d/ Tìm vận tốc của vật khi vừa chạm đất.

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 24 :

Một vật được ném ngang ở độ cao h sau 2 giây với vận tốc ban đầu là 25 m/s .Tầm ném xa của vật là Lấy g=10 m/s²

A 25m
B 40m
C 50m
D 30 m

Đáp án: C

Phương pháp giải:

Áp dụng công thức tính tầm ném xa của vật ném ngang $L = {v_0}\sqrt {\frac{{2h}}{g}} $

Lời giải chi tiết:

Đáp án C

Chiều cao h là $h = \frac{1}{2}g{t^2} = \frac{1}{2}{.10.2^2} = 20m$

Tầm ném xa của vật là $L = {v_0}\sqrt {\frac{{2h}}{g}} = 25.\sqrt {\frac{{2.20}}{{10}}} = 50m$

Đáp án - Lời giải

Câu hỏi 25 :

Từ đỉnh tháp cao 80 m so với mặt đất, ném một vật nhỏ theo phương ngang với vận tốc ban đầu v₀= 30 m/s. Bỏ qua lực cản không khí. Lấy g = 10 m/s²_.

a, Tính thời gian chuyển động của vật đến khi chạm đất.

b, Xác định tầm bay xa của vật.

c, Vẽ quĩ đạo đường đi của vật.

Lời giải chi tiết:

a. Thời gian chuyển động của vật: $t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2 \times 80}}{{10}}} = 4s.$

b. Tầm bay xa: $s = {\nu _o}t = 30 \times 4 = 120m.$

c.

Đáp án - Lời giải

Câu hỏi 26 :

Một máy bay đang bay theo phương ngang với tốc độ 150 m/s, ở độ cao 490 m thì thả một gói hàng xuống đất. Lấy g = 9,8m/s² . Tầm bay xa của gói hàng là :

A 1000 m.
B 7500 m.
C 15000 m.
D 1500 m

Đáp án: D

Phương pháp giải:

Áp dụng công thức tính tầm xa của vật ném ngang $L = {v_0}\sqrt {\frac{{2h}}{g}} $

Lời giải chi tiết:

Đáp án D

Tầm bay xa của gói hàng là $L = {v_0}\sqrt {\frac{{2h}}{g}} = 150.\sqrt {\frac{{2.490}}{{9,8}}} = 1500m$

Đáp án - Lời giải

Câu hỏi 27 :

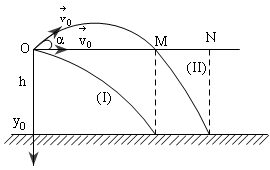
Trên cùng một đường thẳng đứng, người ta ném đồng thời hai vật theo phương ngang. Vật A ở độ cao h₁, vật B độ cao h₂ (so với sàn nằm ngang) với các vận tốc ban đầu tương ứng là v₀₁ và v₀₂. Bỏ qua mọi lực cản. Lấy g=10m/s².

a. Cho h₁=80m và v₀₁=10m/s. Viết phương trình quỹ đạo của vật A. Tìm khoảng cách từ vị trí ném vật A đến điểm mà vật A chạm sàn lần đầu tiên.

b. Vật B va chạm đàn hồi với sàn (vận tốc tuân theo quy luật phản xạ gương), nẩy lên và rơi xuống sàn lần thứ hai cùng một vị trí và cùng thời điểm với vật A chạm sàn lần đầu tiên. Tìm tỉ số $\frac{{{v}_{01}}}{{{v}_{02}}}$và $\frac{{{h}_{1}}}{{{h}_{2}}}$.

Phương pháp giải:

Khảo sát chuyển động của một vật ném ngang

Lời giải chi tiết:

a. Chọn hệ trục Oxy như hình vẽ, gốc O trùng với vị trí ban đầu của vật A, trục Oy thẳng đứng hướng xuống dưới.

Phương trình quỹ đạo của vật A: ${{y}_{1}}=\frac{g}{2.v_{01}^{2}}.x_{1}^{2}$ =>${{y}_{1}}=\frac{x_{1}^{2}}{20}\left( m \right)$

Khoảng thời gian từ lúc vật A chuyển động đến thời điểm vật A chạm sàn lần đầu: ${{y}_{1}}=\frac{g}{2}{{t}^{2}}$ => ${{t}_{1}}=\sqrt{\frac{2{{h}_{1}}}{g}}=4s$

Khoảng cách từ vị trí ném vật A đến điểm mà vật A chạm sàn lần đầu tiên: ${{x}_{1}}={{v}_{01}}.t$ => $L=10.4=40m$

b. Thời gian vật B va chạm sàn lần đầu: ${{t}_{2}}=\sqrt{\frac{2{{h}_{2}}}{g}}$

Vị trí vật 2 chạm sàn lần 1: x_2C= v₀₂. $\sqrt{\frac{2{{h}_{2}}}{g}}$

Vận tốc của vật B khi va chạm với sàn lần thứ nhất : v_x = v_01;v_y = g.t₂ =$\sqrt{2g{{h}_{2}}}$

Sau khi va chạm lần thứ nhất tại C, vì vận tốc tuân theo quy luật phản xạ gương nên tại C vật tiếp tục chuyển động ném xiên với các thành phần vận tốc v_{xc =}= v₀₁và v_yc= -$\sqrt{2g{{h}_{2}}}$ có hướng như hình vẽ.

Phương trình chuyển động vật 2 sau khi va chạm lần thứ nhất: x₂ = x_2c + v_xc.t^’

$\begin{array}{l}
{y_2} = {v_{yC}}.t' + \frac{{gt{'^2}}}{2}\\
= > {y_2} = - \sqrt {2g{h_2}} t' + \frac{{gt{'^2}}}{2}
\end{array}$

(t^’ là khoảng thời gian vật chuyển động từ thời điểm ở điểm C)

Vị trí vật B chạm sàn lần 2:${{x}_{2}}=$ v₀₂. $\sqrt{\frac{2{{h}_{2}}}{g}}$+ v₀₂.$\left( \sqrt{\frac{2{{h}_{1}}}{g}}-\sqrt{\frac{2{{h}_{2}}}{g}} \right)$

Theo giả thiết: ${{x}_{2}}={{x}_{1}}={{v}_{01}}.\sqrt{\frac{2{{h}_{1}}}{g}}$

v₀₂. $\sqrt{\frac{2{{h}_{2}}}{g}}$+ v₀₂. $\left( \sqrt{\frac{2{{h}_{1}}}{g}}-\sqrt{\frac{2{{h}_{2}}}{g}} \right)$ = ${{v}_{01}}.\sqrt{\frac{2{{h}_{1}}}{g}}$=> v₀₂= v₀₁hay $\frac{{{v}_{01}}}{{{v}_{02}}}=1$

$\begin{array}{l}
{y_2} = - \sqrt {2g{h_2}} \left( {\sqrt {\frac{{2{h_1}}}{g}} - \sqrt {\frac{{2{h_2}}}{g}} } \right) + \frac{g}{2}{\left( {\sqrt {\frac{{2{h_1}}}{g}} - \sqrt {\frac{{2{h_2}}}{g}} } \right)^2} = 0\\
= > - 2\sqrt {{h_2}{h_1}} + 2{h_2} + {h_1} + {h_2} - 2\sqrt {{h_2}{h_1}} = 0\\
= > {h_1} - 4\sqrt {{h_2}{h_1}} + 3{h_2} = 0\\
\Delta ' = {\left( {2\sqrt {{h_2}} } \right)^2} - 3{h_2} = {h_2}\\
\Rightarrow \left[ \begin{array}{l}
{h_1} = \sqrt {{h_2}} \\
{h_1} = 3\sqrt {{h_2}}
\end{array} \right.
\end{array}$

Đáp án - Lời giải

Câu hỏi 28 :

Từ đỉnh tháp cao 80m so với mặt đất, ném một vật nhỏ theo phương ngang với vận tốc ban đầu v₀ =30m/s . Bỏ qua lực cản không khí. Lấy g = 10m/s².

a, tính thời gian chuyển động của vật đến khi chạm đất.

b, xác định tầm bay xa của vật.

Phương pháp giải:

Sử dụng công thức của chuyển động ném ngang

Lời giải chi tiết:

a) Thời gian vật chạm đất là :

$t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2.80}}{{10}}} = 4s$

b) Tầm bay xa là: L = v₀.t = 30.4 = 120 (m)

Đáp án - Lời giải

Câu hỏi 29 :

Một vật được ném ngang từ độ cao h = 80 m với vận tốc đầu v₀ = 20 m/s. Lấy g = 10 m/s². Thời gian và tầm bay xa của vật là:

A 3s và 60m.
B 2s và 40m.
C 1s và 20m.
D 4s và 80m.

Đáp án: D

Phương pháp giải:

Áp dụng công thức tính tầm bay xa và thời gian rời

Lời giải chi tiết:

Ta có:
$\begin{array}{l}
t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2.80}}{{10}}} = 4s\\
L = {v_0}.t = 20.4 = 80m
\end{array}$

Đáp án - Lời giải

Câu hỏi 30 :

Một máy bay đang bay ngang ở độ cao 313,6m với tốc độ 54km/h thì thả một gói hàng. Lấy g = 9,8m/s² . Bỏ qua mọi lực cản.

a. Sau bao lâu thì gói hàng sẽ rơi xuống đất?

b. Vị trí của gói hàng khi chạm đất cách vị trí thả theo phương ngang là bao xa?

A a. t = 8s

b. L = 120m
B a. t = 8s

b. L = 1200m
C a. t = 80s

b. L = 1200m
D a. t = 18s

b. L = 1220m

Đáp án: A

Phương pháp giải:

Áp dụng các kiến thức cho chuyển động ném ngang, vật được ném ở độ cao 313,6 m, với vận tốc theo phương ngang là 54km/h = 15m/s.

Thời gian để vật chạm đất được xác định bởi

$t = \sqrt {\frac{{2h}}{g}} $

Tầm bay xa:

$L = v.t = v.\sqrt {\frac{{2h}}{g}} $

Lời giải chi tiết:

Đổi 54km/h = 15 m/s.

a) Thời gian để vật chạm đất được xác định bởi

$t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2.313,6}}{{9,8}}} = 8s$

b) Tầm bay xa:

$L = v.t = v.\sqrt {\frac{{2h}}{g}} = 15.8 = 120m$

Đáp án - Lời giải

Câu hỏi 31 :

Một người đứng ở một vách đá nhô ra biển và bắn một vật theo phương ngang với tốc độ 18m/s. Vách đá cao 50 m so với mặt nước biển. Lấy g=10 m/s².

a) Sau bao lâu thì vật chạm vào mặt nước ?

b) Tính khoảng cách từ điểm ném A đến điểm chạm mặt nước B ?

A 2s; 74m
B 3,16s; 75,8m
C 4,2s; 56m
D 5,1s; 73,2m

Đáp án: B

Phương pháp giải:

Các công thức trong chuyển động ném ngang :

x = vt ; y = 0,5gt²

- Vật chạm đất/ mặt nước : y = h

- Công thức tính tầm ném xa : $L=v\sqrt{\frac{2h}{g}}$

Lời giải chi tiết:

Chọn hệ trục Oxy có gốc O là vị trí ném, trục Ox theo chiều ném, Oy hướng xuống dưới.

Phương trình chuyển động của vật : x = vt = 18t ; y = 0,5gt² = 5t²

a) Khi vật chạm mặt nước thì : y = h = 50m

Ta có : $5{t^2} = 50m \Rightarrow {t^2} = 10 \Rightarrow t = 3,16s$

b) Tầm xa của vật : $L = v\sqrt {\frac{{2h}}{g}} = 18.\sqrt {\frac{{2.50}}{{10}}} = 57m$

Khoảng cách từ điểm ném A đến điểm chạm mặt nước B là :

$A{B^2} = {L^2} + {h^2} = {57^2} + {50^2} \Rightarrow AB = 75,8m$

Đáp án - Lời giải

Câu hỏi 32 :

Một máy bay đang bay ngang với tốc độ 150 m/s ở độ cao 490m so với mặt đát thì thả một gói hàng xuống đất. Cho gia tốc rơi tự do g = 9,8 m/s². Tầm bay xa của gói hàng bằng

A 5001m
B 1005 m
C 5100 m
D 1500 m

Đáp án: D

Phương pháp giải:

Áp dụng công thức tầm bay xa:

$L = {v_0}.\sqrt {\frac{{2h}}{g}} $

Lời giải chi tiết:

Tầm bay xa:

$L = {v_0}.\sqrt {\frac{{2h}}{g}} = 150.\sqrt {\frac{{2.490}}{{9,8}}} = 1500m$

Chọn D

Đáp án - Lời giải

Câu hỏi 33 :

Một vật được ném ngang ở độ cao h so với mặt đất. Bỏ qua sức cản của không khí và lấy g = 10 m/s². Sau 5s vật chạm đất. Độ cao h bằng

A 100 m
B 140 m
C 125 m
D 80 m

Đáp án: C

Phương pháp giải:

Thời gian chuyển động cho đến khi chạm đất của vật ném ngang từ độ cao h: $t = \sqrt {\dfrac{{2h}}{g}} $

Lời giải chi tiết:

Độ cao h bằng: $h = \dfrac{1}{2}g{t^2} = \dfrac{1}{2}{.10.5^2} = 125m$

Chọn C.

Đáp án - Lời giải

Câu hỏi 34 :

Một máy bay bay theo phương ngang ở cùng độ cao 10 km với tốc độ 720 km/h. Viên phi công phải thả quả bom từ xa cách mục tiêu (theo phương ngang) bao nhiêu để quả bom rơi trúng mục tiêu? Phương trình quỹ đạo của quả bom? Lấy g = 10m/s².

A $L = 894,4m;y = \dfrac{{{x^2}}}{{4000}}\,\,\left( m \right)$
B $L = 8944m;y = \dfrac{{{x^2}}}{{8000}}\,\,\left( m \right)$
C $L = 8944m;y = \dfrac{{{x^2}}}{{4000}}\,\,\left( m \right)$
D $L = 894,4m;y = \dfrac{{{x^2}}}{{8000}}\,\,\left( m \right)$

Đáp án: B

Phương pháp giải:

Tầm ném xa: $L = {v_0}.\sqrt {\dfrac{{2h}}{g}} $

Phương trình quỹ đạo của vật: $y = \dfrac{g}{{2v_0^2}}.{x^2}$

Lời giải chi tiết:

Quả bom được xem như ném ngang có ${v_0} = 720km/h = 200m/s$ từ độ cao h = 10km = 10000m.

Áp dụng công thức tính tầm ném xa ta có: $L = {v_0}.\sqrt {\dfrac{{2h}}{g}} = 200.\sqrt {\dfrac{{2.10000}}{{10}}} \approx 8944m$

Để quả bom rơi trúng mục tiêu viên phi công phải thả quả bom từ xa cách mục tiêu (theo phương ngang) 8944m.

Phương trình quỹ đạo của vật ném ngang:

$y = \dfrac{g}{{2v_0^2}}.{x^2} = \dfrac{{10}}{{{{2.2000}^2}}}.{x^2} = \dfrac{{{x^2}}}{{8000}}\,\,\left( m \right)$

Chọn B.

Đáp án - Lời giải

Câu hỏi 35 :

Một máy bay trực thăng cứu trợ bay với vận tốc không đổi v₀ theo phương ngang ở độ cao 1500 m so với mặt đất. Máy bay chỉ có thể tiếp cận được khu vực cách điểm cứu trợ 2 km theo phương ngang. Lấy g = 9,8 m/s². Để hàng cứu trợ thả từ máy bay tới được điểm cần cứu trợ thì máy bay phải bay với vận tốc bằng:

A 114,31 m/s.
B 11, 431 m/s.
C 228,62 m/s.
D 22,86 m/s.

Đáp án: A

Phương pháp giải:

Tầm ném xa: $L = {v_0}t = {v_0}.\sqrt {\dfrac{{2h}}{g}} $

Lời giải chi tiết:

Hàng cứu trợ thả từ máy bay được coi như là vật ném ngang từ độ cao h = 1500m và có tầm ném xa L = 2m = 2000m.

Áp dụng công thức tính tầm ném xa:

$L = {v_0}.\sqrt {\dfrac{{2h}}{g}} \Rightarrow {v_0} = \dfrac{L}{{\sqrt {\dfrac{{2h}}{g}} }} = \dfrac{{2000}}{{\sqrt {\dfrac{{2.1500}}{{9,8}}} }} = 114,31m/s$

Chọn A.

Đáp án - Lời giải

Câu hỏi 36 :

Một hòn bi lăn dọc theo một cạnh của một mặt bàn hình chữ nhật nằm ngang cao h = 1,25 m. Khi ra khỏi mép bàn, nó rơi xuống nền nhà tại điểm cách mép bàn, nó rơi xuống nền nhà tại điểm cách mép bàn L = 1,50 m (theo phương ngang) ? Lấy g = 10m/s². Thời gian hòn bi rơi là:

A 0,35 s
B 0,125 s
C 0,5 s
D 0,25 s

Đáp án: C

Phương pháp giải:

Thời gian rơi: $t = \sqrt {\dfrac{{2h}}{g}} $

Lời giải chi tiết:

Chuyển động của hòn bi khi rời khỏi mặt bàn coi như là chuyển động ném ngang với độ cao ban đầu h = 1,25 m.

Thời gian rơi của hòn bi là : $t = \sqrt {\dfrac{{2h}}{g}} = \sqrt {\dfrac{{2.1,25}}{{10}}} = 0,5s$

Chọn C.

Đáp án - Lời giải

Câu hỏi 37 :

Một hòn bi lăn dọc theo một cạnh của một mặt bàn hình chữ nhật nằm ngang cao h = 1,25 m. Khi ra khỏi mép bàn, nó rơi xuống nền nhà tại điểm cách mép bàn, nó rơi xuống nền nhà tại điểm cách mép bàn L = 1,50 m (theo phương ngang) ? Lấy g = 10m/s². Tốc độ của viên bi lúc rời khỏi bàn ?

A 4,28 m/s;
B 3 m/s;
C 12 m/s;
D 6 m/s;

Đáp án: B

Phương pháp giải:

Tầm ném xa: $L = {v_0}t = {v_0}.\sqrt {\dfrac{{2h}}{g}} $

Lời giải chi tiết:

Chuyển động của hòn bi khi rời khỏi mặt bàn coi như là chuyển động ném ngang với độ cao ban đầu h = 1,25 m và có tầm ném xa là L = 1,50 m.

Áp dụng công thức tính tầm ném xa:

$L = {v_0}.\sqrt {\dfrac{{2h}}{g}} \Rightarrow {v_0} = \dfrac{L}{{\sqrt {\dfrac{{2h}}{g}} }} = \dfrac{{1,5}}{{\sqrt {\dfrac{{2.1,25}}{{10}}} }} = 3m/s$

Chọn B.

Đáp án - Lời giải

Câu hỏi 38 :

Một vật được ném ngang từ độ cao h ở nơi có gia tốc rơi tự do là g = 10 m/s² với vận tốc ban đầu v₀. Biết sau 2s, véctơ vận tốc của vật hợp với phương ngang góc 30⁰. Tốc độ ban đầu của vật gần nhất giá trị nào sau đây?

A 40 m/s.
B 30 m/s.
C 50 m/s.
D 60 m/s.

Đáp án: B

Phương pháp giải:

Góc hợp bởi vecto vận tốc của vật và phương ngang:$\alpha = \left( {\overrightarrow v ;\overrightarrow {{v_x}} } \right)$với: $\tan \alpha = \dfrac{{{v_y}}}{{{v_x}}} = \dfrac{{gt}}{{{v_0}}}$

Lời giải chi tiết:

Góc hợp bởi vecto vận tốc của vật và phương ngang:$\alpha = \left( {\overrightarrow v ;\overrightarrow {{v_x}} } \right)$với: $\tan \alpha = \dfrac{{{v_y}}}{{{v_x}}} = \dfrac{{gt}}{{{v_0}}}$

Với: $\left\{ \begin{array}{l}g = 10m/{s^2}\\t = 2s\\\alpha = {30^0}\end{array} \right. \Rightarrow \tan \alpha = \dfrac{{gt}}{{{v_0}}} \Rightarrow {v_0} = \dfrac{{gt}}{{\tan \alpha }} = \dfrac{{10.2}}{{\tan 30}} = 34,64m/s$

Chọn B.

Đáp án - Lời giải

Câu hỏi 39 :

Ném vật theo phương ngang ở độ cao 50 m so với mặt đất, lấy g = 9.8 m/s², vận tốc lúc ném là 18 m/s, tính thời gian và vận tốc của vật khi chạm đất.

A $t = 3,2s;v = 36,1m/s$
B $t = 3,2s;v = 46,1m/s$
C $t = 4,2s;v = 36,1m/s$
D $t = 4,2s;v = 46,1m/s$

Đáp án: A

Phương pháp giải:

+ Thời gian chuyển động cho đến khi chạm đất: $t = \sqrt {\dfrac{{2h}}{g}} $

+ Vận tốc chạm đất: ${v_{cd}} = \sqrt {v_0^2 + 2gh} $

Lời giải chi tiết:

Ta có: $g = 9,8{\rm{ }}m/{s^2};{\rm{ }}h = 50{\rm{ }}m;{\rm{ }}{v_0}\; = 18{\rm{ }}m/s$

+ Thời gian của vật khi chạm đất: $t = \sqrt {\dfrac{{2h}}{g}} = \sqrt {\dfrac{{2.50}}{{9,8}}} = 3,2s$

+ Vận tốc chạm đất: ${v_{cd}} = \sqrt {v_0^2 + 2gh} = \sqrt {{{18}^2} + 2.9,8.50} = 36,1m/s$

Chọn A.

Đáp án - Lời giải

Câu hỏi 40 :

Ném vật theo phương ngang với vận tốc 10 m/s từ độ cao 40 m xuống đất. Lấy g = 10 m/s². Phương trình quỹ đạo của vật và toạ độ của vật sau 2s là:

A $y = \dfrac{{{x^2}}}{{50}}\,\,\left( m \right);\,\,\,x = 50m,y = 20m$
B $y = \dfrac{{{x^2}}}{{20}}\,\,\left( m \right);\,\,\,x = 50m,y = 20m$
C $y = \dfrac{{{x^2}}}{{20}}\,\,\left( m \right);\,\,\,x = 20m,y = 20m$
D $y = \dfrac{{{x^2}}}{{50}}\,\,\left( m \right);\,\,\,x = 20m,y = 20m$

Đáp án: C

Phương pháp giải:

+ Phương trình chuyển động của vật ném ngang: $\left\{ \begin{array}{l}x = {v_0}t\,\,\,\,\,\,\,\,\left( 1 \right)\\y = \dfrac{1}{2}g{t^2}\,\,\,\left( 2 \right)\end{array} \right.$

+ Phương trình quỹ đạo: $y = \left( {\dfrac{g}{{2.v_0^2}}} \right).{x^2}$

Lời giải chi tiết:

Ta có: $g = 10m/{s^2};{\rm{ }}h = 40{\rm{ }}m;{\rm{ }}{v_0}\; = 10{\rm{ }}m/s$

+ Phương trình quỹ đạo: $y = \left( {\dfrac{g}{{2.v_0^2}}} \right).{x^2} = \dfrac{{10}}{{{{2.10}^2}}}.{x^2} = \dfrac{{{x^2}}}{{20}}\,\,\left( m \right)$

+ Toạ độ của vật sau 2s là: $\left\{ \begin{array}{l}x = {v_0}t = 10.2 = 20m\\y = \dfrac{1}{2}g{t^2} = \dfrac{1}{2}{.10.2^2} = 20m\end{array} \right.$

Chọn C.

Đáp án - Lời giải

Câu hỏi 41 :

Một vật được ném ngang ở độ cao 20m phải có vận tốc đầu là bao nhiêu để trước lúc chạm đất vận tốc của nó là 25m/s? Biết g = 10m/s².

A 10m/s
B 20m/s
C 15m/s
D 18m/s

Đáp án: C

Phương pháp giải:

Vận tốc chạm đất: ${v_{cd}} = \sqrt {v_0^2 + 2gh} $

Lời giải chi tiết:

Vận tốc chạm đất: ${v_{cd}} = \sqrt {v_0^2 + 2gh} \Rightarrow {v_0} = \sqrt {v_{cd}^2 - 2gh} $

Với: $\left\{ \begin{array}{l}{v_{cd}} = 25m/s\\g = 10m/{s^2}\\h = 20m\end{array} \right.$

Thay số vào ta được: ${v_0} = \sqrt {v_{cd}^2 - 2gh} = \sqrt {{{25}^2} - 2.10.20} = 15m/s$

Vậy vật được ném ngang ở độ cao 20 m phải có vận tốc đầu là 15 (m/s) thì trước lúc chạm đất vật có vận tốc 25m/s.

Chọn C.

Đáp án - Lời giải

Câu hỏi 42 :

Trong một trận đấu bóng chuyền, một vận động viên nhảy lên cao để đập giao bóng từ độ cao h = 3 m đối với mặt đất và đập bóng theo phương ngang, vuông góc với lưới với vận tốc v₀ = 20 m/s. Lấy g = 10 m/s². Bỏ qua lực cản của không khí.

a) Trong trường hợp bóng bay qua lưới, tìm thời gian chuyển động của bóng trong không khí và tầm xa của bóng.

b) Viết phương trình quỹ đạo của bóng.

c) Biết rằng mép trên của lưới cao 2,24 m đối với mặt đất và bóng vừa qua sát mép trên của lưới. Hỏi vận động viên đứng cách lưới theo phương ngang một khoảng bao nhiêu?

Phương pháp giải:

Chuyển động của bóng là chuyển động của vật bị ném ngang từ độ cao h.

Thời gian chuyển động của bóng: $t=\sqrt{\frac{2h}{g}}$

Tầm xa của bóng: $L={{v}_{0}}t={{v}_{0}}\sqrt{\frac{2h}{g}}$

Phương trình quỹ đạo của bóng: $y=\frac{g}{2{{v}_{0}}^{2}}{{x}^{2}}$

Lời giải chi tiết:

a) Thời gian chuyển động của bóng là: $t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2.3}{10}}=0,77\,\,\left( s \right)$

Tầm xa của bóng là: $L={{v}_{0}}t={{v}_{0}}\sqrt{\frac{2h}{g}}=20.\sqrt{\frac{2.3}{10}}=15,49\,\,\left( m \right)$

b) Phương trình quỹ đạo của bóng là: $y=\frac{g}{2{{v}_{0}}^{2}}{{x}^{2}}=\frac{10}{{{2.20}^{2}}}{{x}^{2}}=\frac{1}{80}{{x}^{2}}$

c) Thay y = 2,24 m vào phương trình quỹ đạo, ta có:

$2,24=\frac{1}{80}{{x}^{2}}\Rightarrow x=13,39\,\,\left( m \right)$

Vậy vận động viên đứng cách lưới theo phương ngang một khoảng 13,39 m.

Đáp án - Lời giải

Câu hỏi 43 :

Một máy bay bay ngang với tốc độ 150m/s, ở độ cao 490m thì thả một gói hàng xuống đất. Lấy g = 9,8m/s². Tầm bay xa của gói hàng là :

A 7500m
B 15000m
C 1500m
D 1000m

Đáp án: C

Phương pháp giải:

Tầm ném xa: $L = {v_0}t = {v_0}.\sqrt {\dfrac{{2h}}{g}} {\rm{ }}$

Lời giải chi tiết:

Gói hàng thả từ máy bay được coi như là vật ném ngang từ độ cao h = 490m với vận tốc ban đầu ${v_0} = 150m/s$

Tầm bay xa của gói hàng là:

$L = {v_0}t = {v_0}.\sqrt {\dfrac{{2h}}{g}} = 150.\sqrt {\dfrac{{2.490}}{{9,8}}} = 1500m$

Chọn C.

Đáp án - Lời giải

Câu hỏi 44 :

Ném vật theo phương ngang từ đỉnh dốc nghiêng góc 30⁰ với phương ngang. Lấy g = 10 m/s². Nếu vận tốc ném là 10m/s, vật rơi ở một điểm trên dốc, tính khoảng cách từ điểm ném đến điểm rơi.

A $\dfrac{{20\sqrt 3 }}{3}m$
B $\dfrac{{40\sqrt 3 }}{3}m$
C $\dfrac{{20}}{3}m$
D $\dfrac{{40}}{3}m$

Đáp án: D

Phương pháp giải:

Phương trình quỹ đạo: $y = \left( {\dfrac{g}{{2.v_0^2}}} \right).{x^2}$

Áp dụng tỉ số lượng giác và định lí Pi – ta – go trong tam giác vuông.

Lời giải chi tiết:

Ta có: $\left\{ \begin{array}{l}{v_0}\; = 10{\rm{ }}m/s\\g = 10{\rm{ }}m/{s^2}\\\alpha = {30^0}\end{array} \right.$

Giả sử vật rơi tại điểm A ở trên dốc có toạ độ (x; y) như hình vẽ:

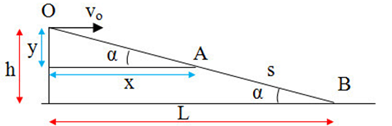
Phương trình quỹ đạo: $y = \left( {\dfrac{g}{{2.v_0^2}}} \right).{x^2} = \dfrac{{10}}{{{{2.10}^2}}}.{x^2} \Leftrightarrow y = 0,05{x^2}\,\left( m \right)\,\,\,\,\left( 1 \right)$

Từ hình vẽ ta có: $\tan \alpha = \dfrac{y}{x} \Leftrightarrow \tan 30 = \dfrac{y}{x} \Rightarrow x = \sqrt 3 y\,\,\left( 2 \right)$

Từ (1) và (2) ta có hệ phương trình: $\left\{ \begin{array}{l}y = 0,05{x^2}\\x = \sqrt 3 y\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = \dfrac{{20\sqrt 3 }}{3}m\\y = \dfrac{{20}}{3}m\end{array} \right.$

Khoảng cách từ điểm ném đến điểm rơi: $OA = \sqrt {{x^2} + {y^2}} = \sqrt {{{\left( {\dfrac{{20\sqrt 3 }}{3}} \right)}^2} + {{\left( {\dfrac{{20}}{3}} \right)}^2}} = \dfrac{{40}}{3}m$

Chọn D.

Đáp án - Lời giải

Câu hỏi 45 :

Ném vật theo phương ngang từ đỉnh dốc nghiêng góc 30⁰ với phương ngang. Lấy g = 10 m/s². Nếu dốc dài 15m thì vận tốc ném là bao nhiêu để vật rơi ngoài chân dốc?

A ${v_0} > 13m/s$
B ${v_0} > 10,6m/s$
C ${v_0} > 11,6m$
D ${v_0} > 12m/s$

Đáp án: B

Phương pháp giải:

Tầm ném xa: ${x_{\max }} = {v_0}.t = {v_0}.\sqrt {\dfrac{{2h}}{g}} $

Vật rơi ngoài chân dốc khi tầm ném xa của vật lớn hơn chiều dài con dốc theo phương ngang.

Lời giải chi tiết:

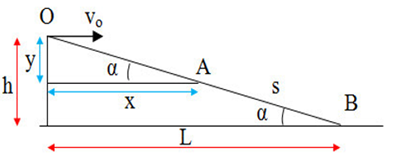
Ta có: $\left\{ \begin{array}{l}OB\; = 15{\rm{ }}m\\g = 10{\rm{ }}m/{s^2}\\\alpha = {30^0}\end{array} \right.$

Từ hình vẽ ta có: $\left\{ \begin{array}{l}L = OB.\cos 30 = 15.\cos 30 = 13m\\h = OB.\sin 30 = 15.\sin 30 = 7,5{\rm{ }}m\end{array} \right.$

Vật rơi ngoài chân dốc khi :

$\begin{array}{l}{x_{\max }} > L \Leftrightarrow {v_0}.\sqrt {\dfrac{{2h}}{g}} > L \Rightarrow {v_0} > \dfrac{L}{{\sqrt {\dfrac{{2h}}{g}} }} = \dfrac{{13}}{{\sqrt {\dfrac{{2.7,5}}{{10}}} }} = 10,6m/s\\ \Rightarrow {v_0} > 10,6m/s\end{array}$

Chọn B.

Đáp án - Lời giải

50 bài tập Bài toán về chuyển động ném ngang mức độ vận dụng

Báo lỗi góp ý